poj 3159 Candies （差分约束）

一个叫差分约束系统的东西。如果每个点定义一个顶标x(v)，x(t)-x(s)将对应着s-t的最短路径。

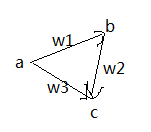
比如说w+a≤b，那么可以画一条a到b的有向边，权值为w，同样地给出b+w2≤c，a+w3≤c。那么a到c的最大差就受这些不等式约束，对应着图中的最短路。

这个边多，不要用vector存，满了以后重新复制数据，会T的，没试过指定大小。。。

#include<iostream>
#include<cstdio>
#include<vector>
#include<cstring>
#include<queue>
using namespace std;
//POJ 是个坑
const int maxn = 3e4+1;
const int maxm = 15e4+5;
struct Edge
{
    int v,w,nxt;
    //Edge(int v = 0,int w = 0):v(v), w(w){}
}edges[maxm];

int ecnt,head[maxn];

typedef pair<int,int> Node;
#define fi first
#define se second

void addEdge(int u,int v,int w)
{
    edges[++ecnt].v = v;
    edges[ecnt].w = w;
    edges[ecnt].nxt = head[u];
    head[u] = ecnt;
}

int d[maxn];

const int INF = 0x7f7f7f7f;

int dijkstra(int s, int t)
{
    priority_queue<Node,vector<Node>,greater<Node> > q;
    memset(d,0x7f,sizeof(d));
    q.push(Node(d[s] = 0,s));
    while(q.size()){
        Node x = q.top(); q.pop();
        int u = x.se;
        if(u == t) return d[t];
        if(x.fi != d[u]) continue;
        for(int i = head[u]; i; i = edges[i].nxt){
            Edge &e = edges[i];
            if(d[e.v] - d[u] > e.w){
                d[e.v] = d[u] + e.w;
                q.push(Node(d[e.v],e.v));
            }
        }
    }
    return INF;
}

int main()
{
    //freopen("in.txt","r",stdin);
    int n,m; cin>>n>>m;
    while(m--){
        int u,v,w; scanf("%d%d%d",&u,&v,&w);
        addEdge(u-1,v-1,w);
    }
    printf("%d
",dijkstra(0,n-1));
    return 0;
}