Aizu 2456 Usoperanto （贪心）

贪心，对于一个修饰关系可以连一条有向边，在合并的时候，子节点的序列一定是连续安排的，因为如果有交叉，交换以后一定更优。

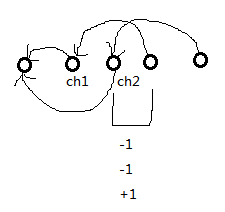
然后一个序列一个序列的考虑，长度短的应该在前面，否则同样交换以后更优。因此排序以后统计就行了。

数据理论最多递归1e6层，dfs爆栈了，手写栈模拟递归。。。

#include<bits/stdc++.h>
using namespace std;

const int maxn = 1e6+5;

vector<int> G[maxn];
int M[maxn];
typedef long long ll;
long long ans;
bool cmp(int a,int b) { return M[a] < M[b]; }

struct Frame
{
    int u,i;
};
stack<Frame> dfs;
inline void CreatFrame(int u){ dfs.push({u,0});}

#define PS push
void DFS(int s)
{
    CreatFrame(s);
    bool pre = true;//pre or post
    while(dfs.size()){
        loop:
        int u = dfs.top().u, &i = dfs.top().i;
        for(; i < (int)G[u].size(); i++){
            if(pre) {
                CreatFrame(G[u][i]);
                goto loop;
            }
            M[u] += M[G[u][i]];
            pre = true;
        }
        sort(G[u].begin(),G[u].end(),cmp);
        for(int i = 0; i < (int)G[u].size(); i++){
            ans += M[G[u][i]]*((ll)G[u].size()-i-1);
        }
        dfs.pop(); pre = false;
    }
}
int rts[maxn];

//#define LOCAL
int main()
{
#ifdef LOCAL
    freopen("in.txt","r",stdin);
#endif
    int n; scanf("%d",&n);
    int c = 0;
    for(int i = 0; i < n; i++){
        int f; scanf("%d%d",M+i,&f);
        if(~f){ G[f].push_back(i); }
        else rts[c++] = i;
    }
    while(c--){
        DFS(rts[c]);
    }
    printf("%lld
",ans);
    return 0;
}

另外拓扑排序也可以避免递归

#include<bits/stdc++.h>
using namespace std;

const int maxn = 1e6+5;

int hd[maxn],nx[maxn],to[maxn],ec;

void add(int u,int v)
{
    nx[++ec] = hd[u];
    to[ec] = v;
    hd[u] = ec;
}

int M[maxn];
int fa[maxn],deg[maxn];

typedef long long ll;

int stk[maxn];
int q[maxn];

//#define LOCAL
int main()
{
#ifdef LOCAL
    freopen("in.txt","r",stdin);
#endif
    int n; scanf("%d",&n);
    int rt = 0;
    for(int i = 0; i < n; i++){
        int f; scanf("%d%d",M+i,&f);
        if(~f){
            add(f,i); deg[f]++;
        }
        fa[i] = f;
    }
    int frnt = 0, tail = 0;
    for(int i = 0; i < n; i++){
        if(!deg[i]) q[tail++] = i;
    }
    long long ans = 0;
    while(frnt<tail){
        int u = q[frnt++];
        int top = 0;
        for(int i = hd[u]; i; i = nx[i]){
            stk[top++] = M[to[i]];
        }
        sort(stk,stk+top);
        for(int i = 0; i < top; i++){
            ans += stk[i]*(ll)(top-i-1);
        }
        if(~fa[u]){
            M[fa[u]] += M[u];
            if(!--deg[fa[u]])  q[tail++] = fa[u];
        }
    }
    printf("%lld
",ans);
    return 0;
}