题面简述
在坐标系的第一象限中画(n)个矩阵(每个矩阵的边与坐标系平行),问有多少面积被恰好(k)个矩阵覆盖
(40pts)思路简述
由于矩阵右上角最多到((1000,1000)),所以可以直接建一个(1000 imes1000)的数组模拟
(40pts)代码
代码很易懂就不放注释了
#include<iostream>
using namespace std;
int map[1005][1005];
int main()
{
int n,k;
int cnt=0;
cin>>n>>k;
for(int i=0;i<n;i++)
{
int x1,y1,x2,y2;
cin>>x1>>y1>>x2>>y2;
for(int x=x1;x<x2;x++)
for(int y=y1;y<y2;y++)
map[x][y]++;
}
for(int i=1;i<=1000;i++)
for(int j=1;j<=1000;j++)
if(map[i][j]==k)
cnt++;
cout<<cnt;
return 0;
}
正文开始
(100pts)思路简述
有没有用几个数字来表示数组中被覆盖矩阵个数的方式
当然有了
用前缀和啊
我们要牵一发而动全身,以点代面
在做前缀和相关的题目时,我们关注的都是怎么计算出某一段的和
而这题我们可以换个角度来想
我们将(x1)设为(2),将(y1)设为(2),将(x2)设为(5),将(y2)设为(4)
众所周知
在二维前缀和中,一旦(a_{2,2})增加一,(f_{2,2})、(f_{3,2})、(f_{2,3})一直到(f_{infty,infty})都会增加一
不会吧,不会吧,不会还有人不知道a是原数组而f是前缀和数组吧
在上句中,(a_{2,2})增加一就可以看作在((2,2))到((infty,infty))画了一个矩阵(在(f)数组中)
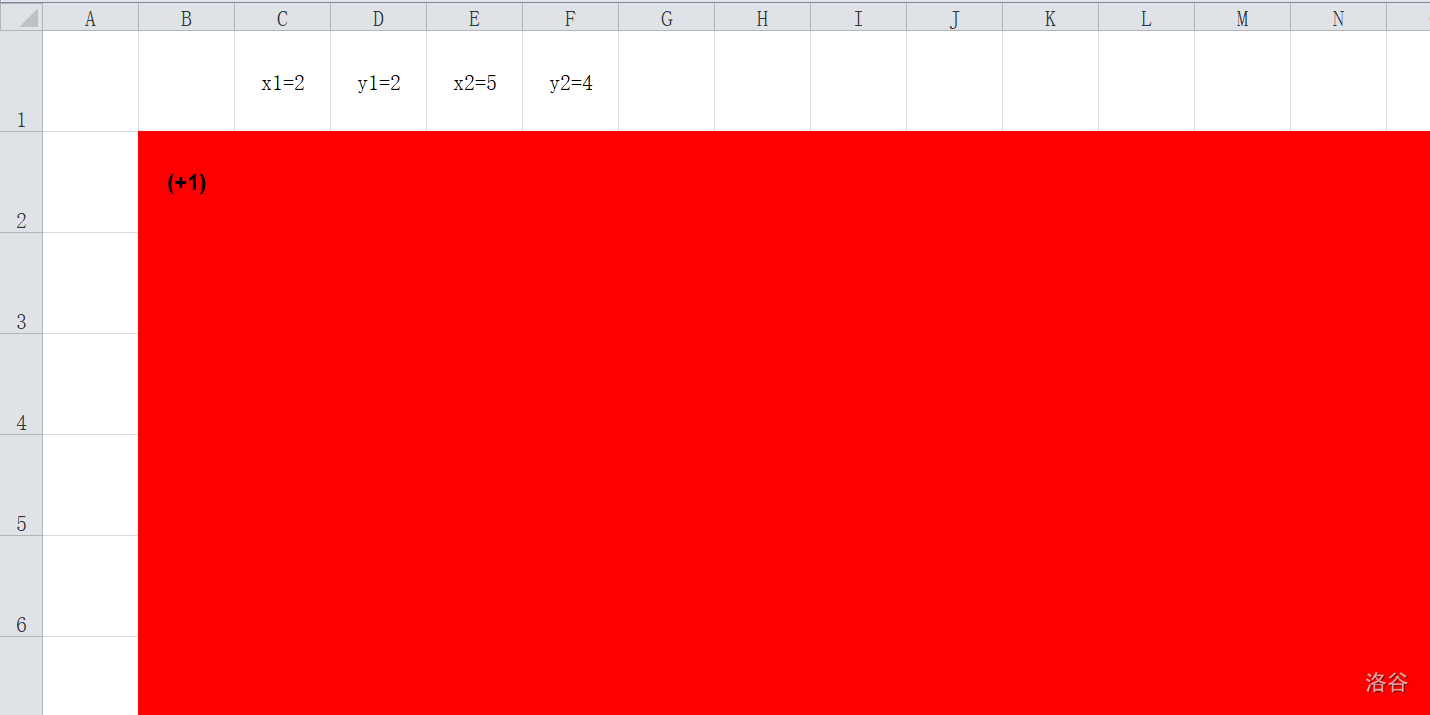
而我们要画的并不是一个((x1,y1))到((infty,infty))的矩阵
怎么剪掉多余部分呢?
直接减不就完了
反过来(指“众所周知”后一句),一旦(a_{5,2})减少一,(f_{5,2})一直到(f_{infty,infty})也都会减少一
在上句中,(a_{4,2})减少一就可以看作在((5,2))到((infty,infty))抹掉了一个矩阵(在(f)数组中)
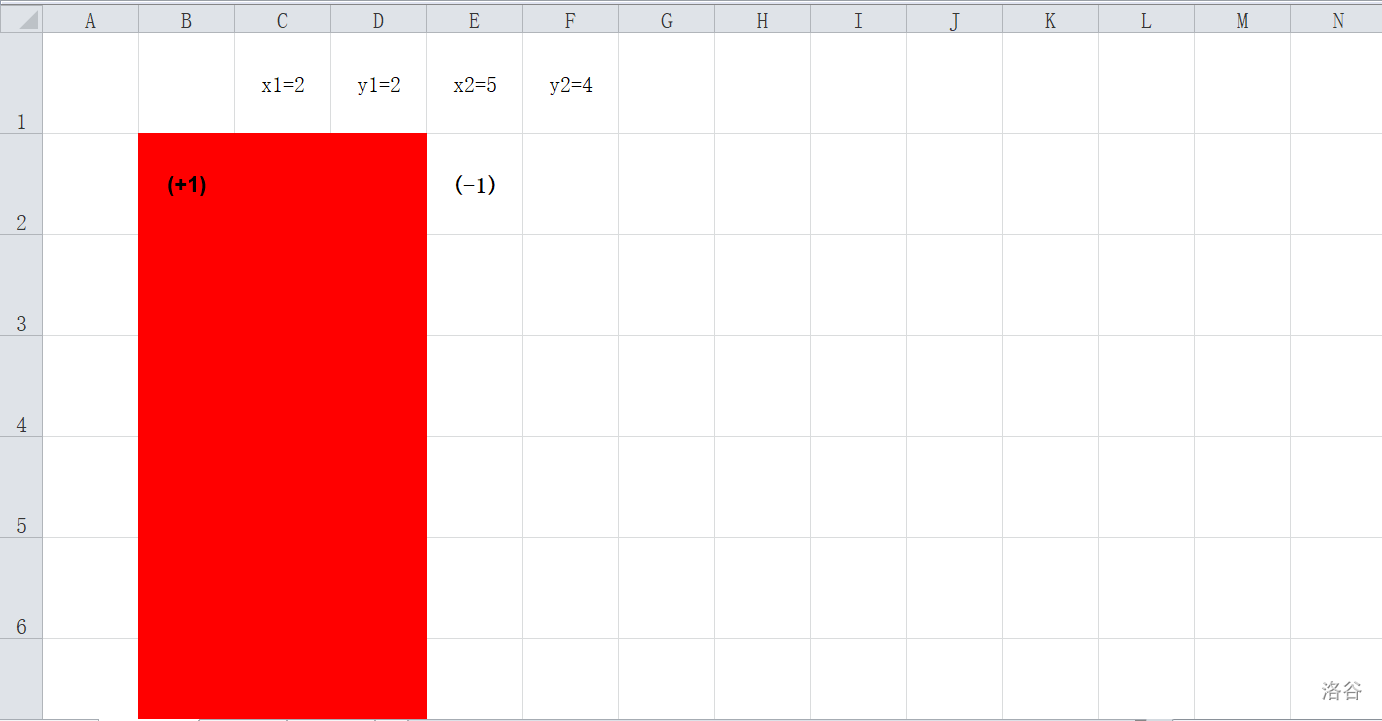
而在(a_{2,4})减少一就可以看作在((2,4))到((infty,infty))抹掉了一个矩阵(在(f)数组中)
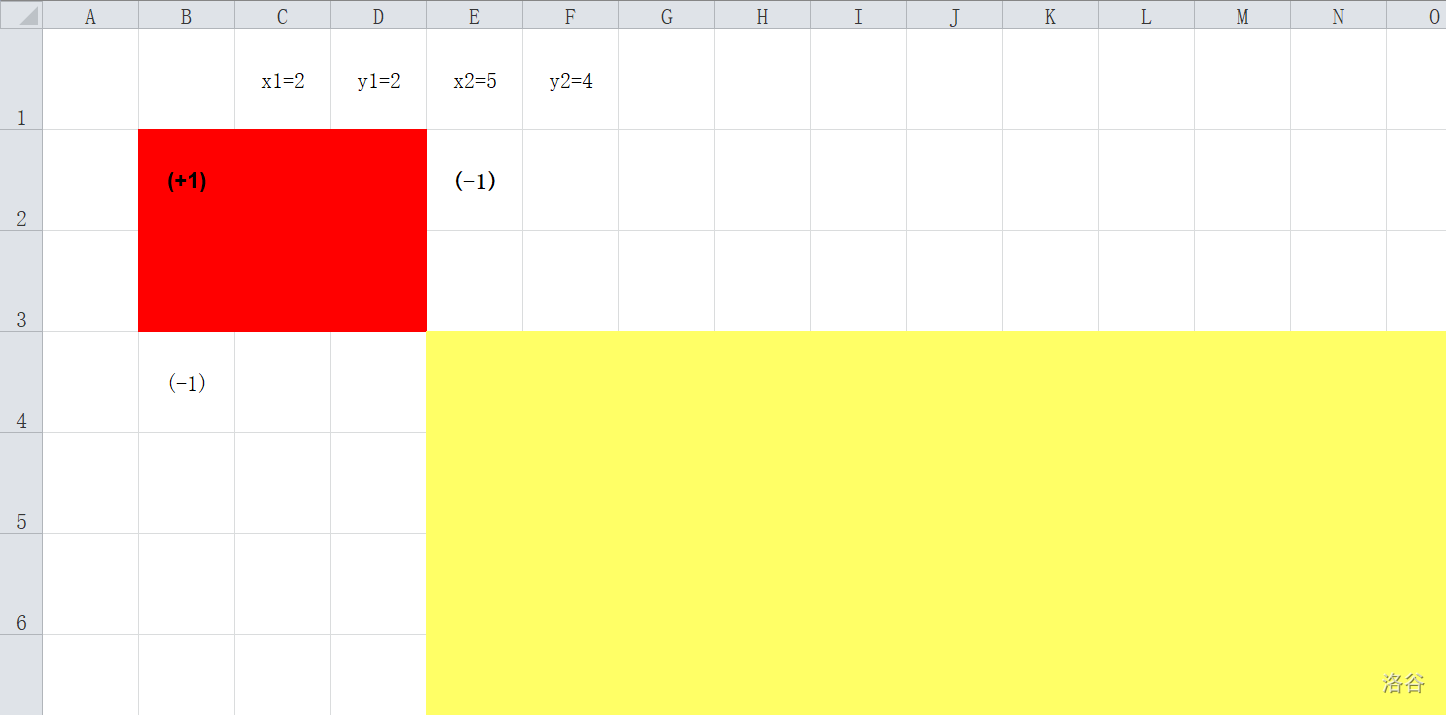
那么这个时候,聪明的小朋友就会发现了,在((5,4))到((infty,infty))多抹去了一个矩阵!
我们在(a_{5,4})增加一就能把这个多减的矩阵补回来
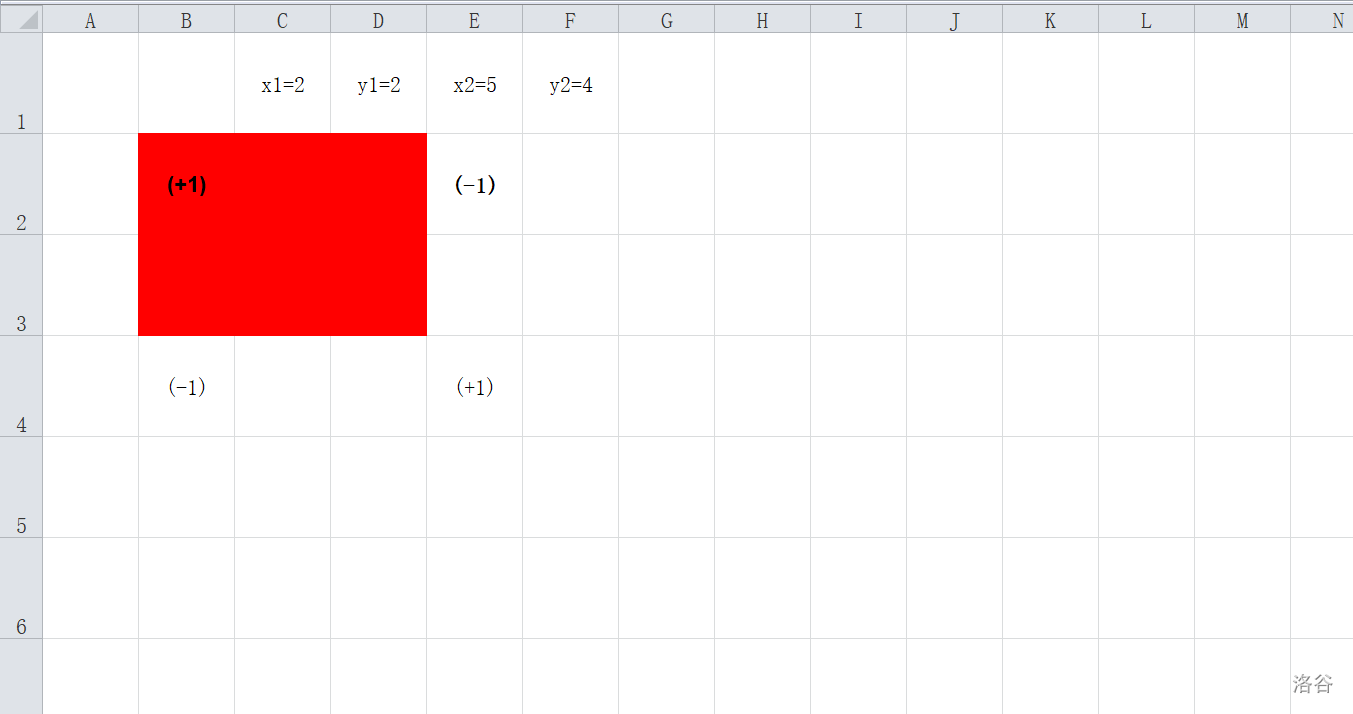
我们只用改动4个变量就能表示出一层被覆盖的矩阵
用题目中给出的量顺一下:
要想在加载前缀和数组时加载出矩阵的覆盖情况,我们可以改动四个位置
((x1,y1))(加一)、((x1,y2))(减一)、((x2,y1))(减一)和((x2,y2))(加一)
(a_{x1,y1})加一得到((x1,y1))到((infty,infty))的大矩阵
(a_{x1,y2})与(a_{x2,y1})减一的目的是减去大矩阵多余的部分,但会多减
(a_{x2,y2})加一补上了多减的部分
按照这种方法加载出存储着所有矩阵覆盖信息的(a)数组,再加载出(f)前缀和数组,顺便在加载时计算出覆盖了(k)层的面积
(100pts)代码
#include<iostream>
using namespace std;
long long a[1005][1005];//为了省空间将“f”数组与“a”数组合二为一
int main()
{
int n,k;
int cnt=0;
cin>>n>>k;
for(int i=0;i<n;i++)
{
int x1,y1,x2,y2;
cin>>x1>>y1>>x2>>y2;
a[x1][y1]++;
a[x1][y2]--;
a[x2][y1]--;
a[x2][y2]++;//将矩阵存入数组
}
for(int i=0;i<=1000;i++)
for(int j=0;j<=1000;j++)
{
if(!i&&!j)
continue;
if(!i)
a[i][j]+=a[i][j-1];
else if(!j)
a[i][j]+=a[i-1][j];//以上六行均为判断边界
else
a[i][j]+=a[i][j-1]+a[i-1][j]-a[i-1][j-1];
if(a[i][j]==k)
cnt++;//判断正好覆盖k层的面积
}
cout<<cnt;
return 0;
}
都看到这里了,不留下个赞么
死皮赖脸.jpg