首先假设:每个矩阵对应一个加权二分图。所谓「图」是指顶点(点)和线的集合;「二分」是指点有两种不同的类型/颜色;「加权」是指每条线都有一个数字标记。

上图对应一个 3×2 矩阵 M。右侧三个绿点,分别对应矩阵 M 的三行,两个粉点分别对应矩阵 M 的两列。如果对应矩阵 M 中的值非零,就在绿点和粉点间画一条线连接 。

例如,在第二个绿点和第一个粉点间存在一条线,因为 M_21=4,即矩阵 M 第二行第一列的值不为 0。此外,用非零数字标记了这条线。而第一个绿点和第二个粉点之间没有线连接,因为矩阵的第一行第二列值为零。
更明确的描述如下:
任何矩阵 M 都是 n×m 个数的数组。但是这样的数组也可以看作函数 M:X×Y→R,其中 X = {x_1,...,x_n},是一组 n 个元素组成的集合;Y = {y_1,...,y_m},是一组 m 个元素组成的集合。实际上,如果要描述矩阵 M,那么需要描述第 ij 项的值。换句话说,对于每对 (i,j),都需要给出一个实数 M_ij。函数 M:X×Y→R 关联每对 (x_i,y_j)(如果愿意,可以去掉字母并将其看作 (i,j)),即实数 M(x_i,y_j)。所以可以将 M(x_i,y_j) 简写为 M_ij。因此,矩阵就是一种函数。

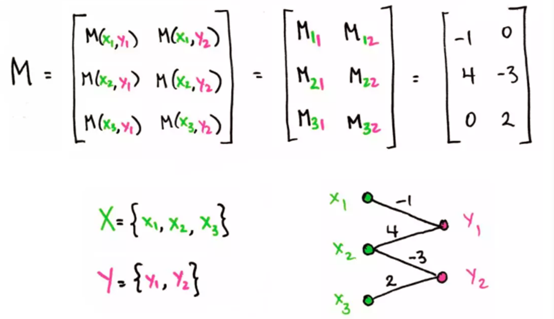
如前所述,进一步认为 X 的元素是绿点,而 Y 的元素是粉点。然后矩阵 M 以下图方式与加权二分图相对应:图的顶点有由 X 和 Y 提供的两种不同颜色,并且每个 x_i 和 y_j 之间存在连线,连线由数字 M_ij 标记。但是如果数值为零,那就省略这条边。
每个矩阵对应一个图。当以这种方式可视化矩阵时,神奇的事就发生了。
矩阵乘法即为沿连线向前运算:
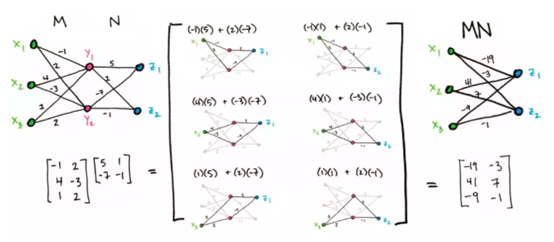
给定两个矩阵(图)M:X×Y→R 和 N:Y×Z→R,可以通过将它们的图拼在一起并沿着连线进行乘法运算:MN 的第 ij 项的输入,即连接 x_i 到 z_j 的线的值,是通过将沿 x_i 到 z_j 的各个边相乘并加和得到的。例如:
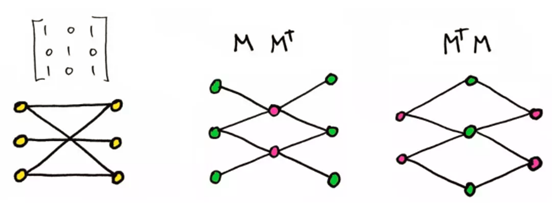
对称矩阵对应对称图:
如果一个矩阵等于它的转置,即为对称矩阵。这种对称性常通过矩阵对角线映射得到。但现在可以从图中观察到对称性。尤其对于任何矩阵 M 来说,下图直观地解释了为什么MMT和 MTM 始终对称!
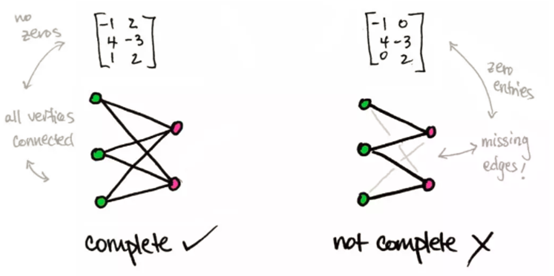
若矩阵所有项都非零,则对应完全二分图。
如果一个矩阵的所有元素都不为零,那么它对应的图就没有缺失的连线。这意味着 X 中的每个点都与 Y 的每个点相连。这样的二分图称为完全二分图。
N 分块矩阵对应独立的 N 个图。
具体来说,由直和得到的分块矩阵对应断开的图。将两个矩阵做直和运算得到更大的数组(与向量直和运算类似),即一个带有全零块的大型分块矩阵。分块矩阵的图通过将原矩阵的图叠加得到。

事实证明,概率非常适合矩阵-图的讨论。这是通过另一个有趣的小事实来实现的:

例如:

这样的概率分布图可以让更好地分析:
联合概率
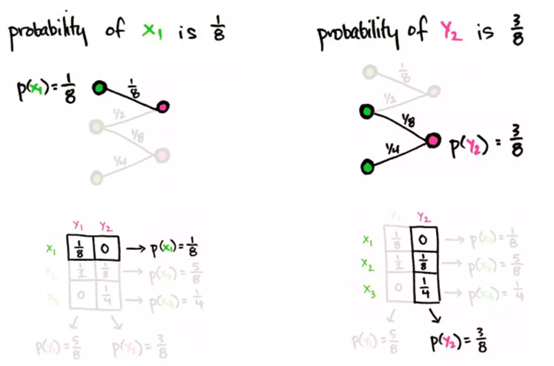
通过架构图中的连线,可以得到联合概率:(x_i,y_j) 的概率是连接 x,y 两点的线的标签。

边缘概率
边缘概率是通过沿矩阵的行/列求和得到的(与上图等效)。例如,x_1 的概率 p(x_1)=p(x_1,y_1)+p(x_1,y_2)=1/8+0,这是第一行的总和。同样,y_2 的概率是 p(y_2)=p(x_1,y_2)+p(x_2,y_2)+p(x_3,y_2)=0+1/8+1/4,是第二列的和。
图中,x_i 的边缘概率是以 x_i 为顶点的所有连线的和。类似地,y_j 的边缘概率是以 y_j 为顶点的所有连线的和。
条件概率
条件概率是由联合概率除以边缘概率得到的。例如在 y_2 条件下 x_3 的概率 p(x_3|y_2)=p(x_3,y_2)/p(y_2)。从图中可以看出,这是通过将 x_3 和 y_2 的连线除以所有与 y_2 相连的线之和得到的。同样,y_i 下 x_j 的条件概率是两点连线的值除以所有与 x_j 相连的线之和。
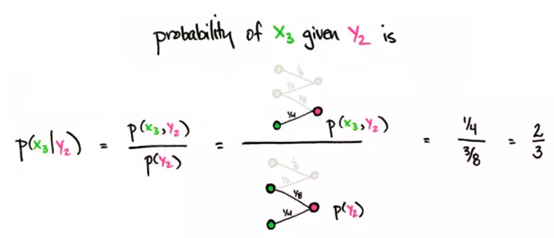
图化的原理并不复杂,只是有时用新角度看待旧想法。
关系矩阵
另一个简单而有趣的事实,即:矩阵运算在交换环(communicative ring)上是有意义的。不仅仅是像 R 或 C 等。矩阵相乘甚至不需要负数:矩阵运算在交换半环上是有意义的!(半环是一个没有相反数的环。)
因为包含两个元素 Z_2 = {0,1} 的集合通过下图的加法和乘法形成一个半环:
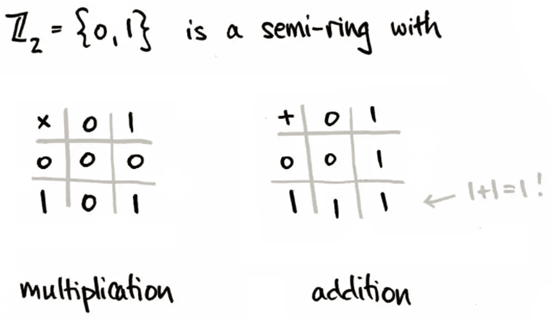
因为一个矩阵 M:X×Y→Z_2 相当于一个「关系」。「关系」是笛卡尔积 X×Y 的子集 R 的名称。换句话说,每个 Z_2-valued 矩阵定义了一个「关系」,每个关系又定义了一个 Z_2-valued 矩阵:当且仅当 (x_i,y_j) 是 R 子集的元素时,M_ij=1,否则 M_ij=0。
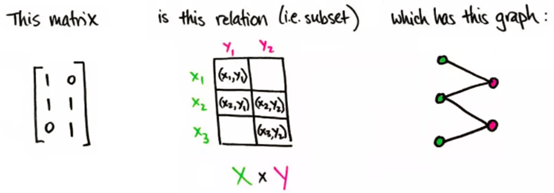
Z_2 中的矩阵图与上面讨论的图完全相同,只是现在所有连线的值都是 0 或 1。如果权重是 0,那和之前一样。
通过将基础(半)环从 R 改为 Z_2,改变了解释权重的方式。例如,在上面的概率场景中,「从 x_1 到 y_1 的概率是多少?」答案由对应边的权重而来,在本例中为 12.5%。或者,当矩阵在 Z_2 中取值时,问题变为:「是否可能从 x_1 到 y_1?」如果连线标记为 1,则为「是」,如果标记为 0 则为「否」。
重要的是,「关系」的组合恰好是使用了上面的 Z_2 算法的矩阵乘法。换句话说,给定任意两个关系 R⊂X×Y 和 S⊂Y×Z,存在一个新关系 SR⊂X×Z,包括所有 (x,z),至少存在一个 y∈Y,其中 (x,y)∈R,(y,z)∈S。这种新关系正是表示 R 和 S 的矩阵乘积所指定的。
原文链接:https://www.math3ma.com/blog/matrices-probability-graphs