折半查找

折半查找

1. 算法思想
2. 算法实现
3. 查找判定树
4. 折半查找效率

折半查找的算法思想

折半查找，又称“二分查找”，仅适用于有序的顺序表

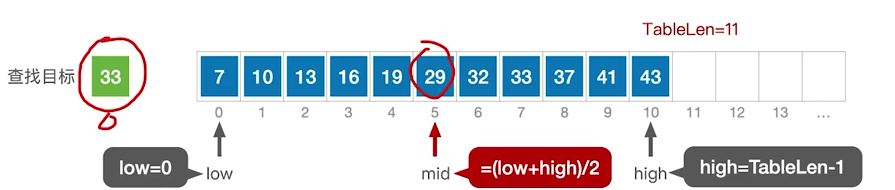
33>mid，往右查

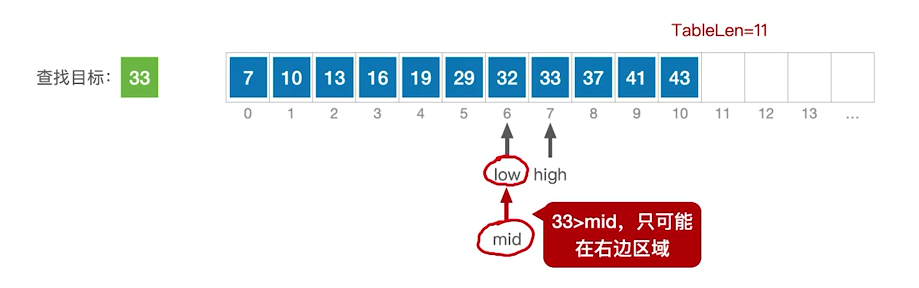
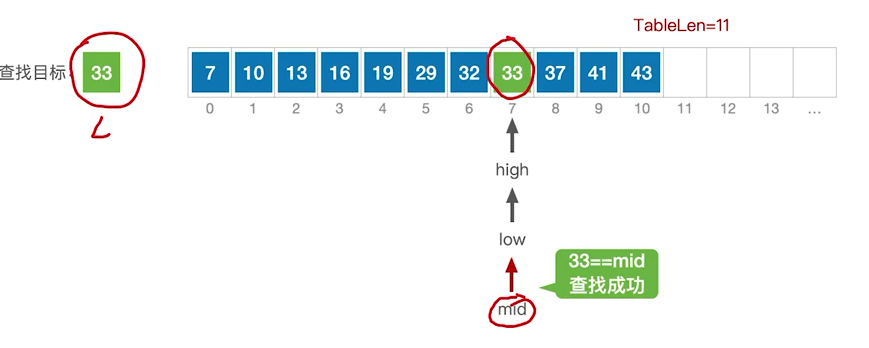
右指针到一个位置就-1，左指针到一个位置就+1

low>high，查找失败

折半查找的实现

typedef struct{
    ElemType *elem;
    int TableLen;
}SSTable;

//折半查找（升序）
int Binary_Search(SSTable L,ElemType key){
    int low = 0,high = L.TableLen-1,mid;
    while(low<=high){
        mid = (low+high)/2;				//取中间位置
        if(L.elem[mid] == key)
            return mid;					//查找成功则返回所在位置
        else if(L.elem(mid)>key)
            high = mid -1;				//从前半部分继续查找
        else
            low = mid +1;				//从后半部分继续查找
    }
    return -1;							//查找失败，返回-1
}

顺序表拥有随机访问的特性，链表没有

查找效率复分析

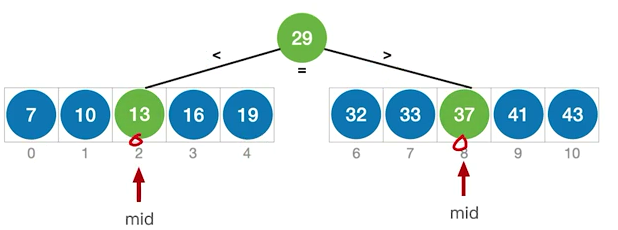
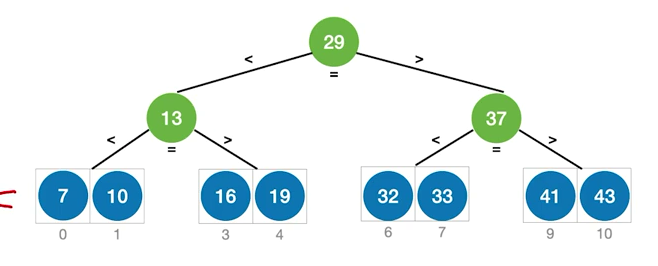
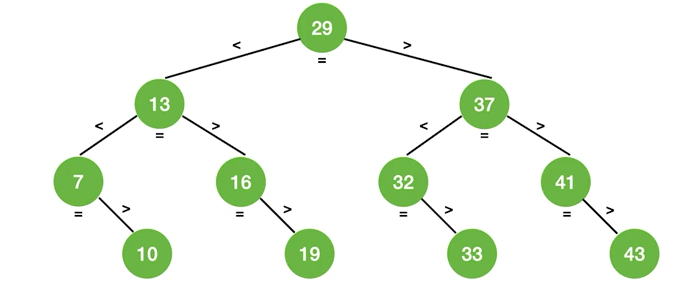
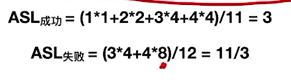
查找判定树的构造

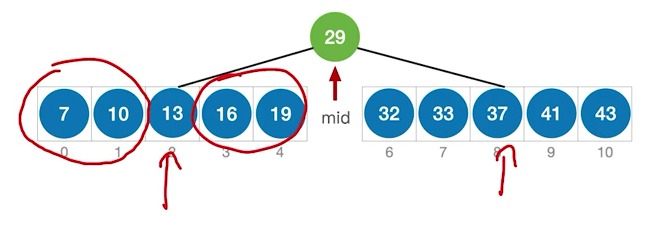
如果当前low和high之间有奇数个元素，则mid分隔后，左右两个部分元素个数相等

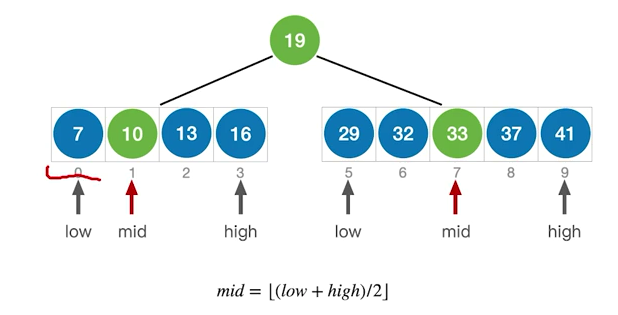
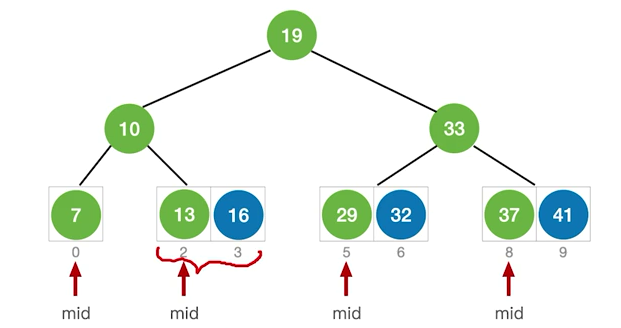
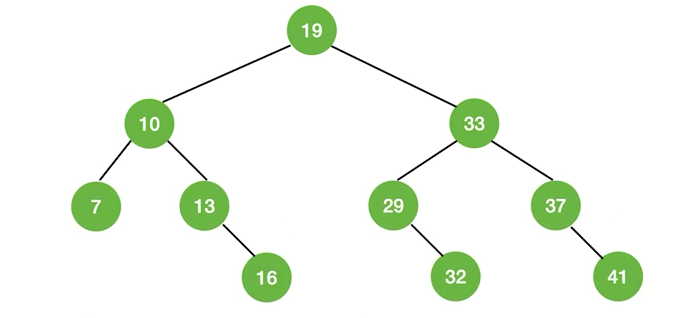
如果当前low和high之间有偶数个元素，则mid分隔后，左半部分比右半部分少一个元素

折半查找的判定树中，若 mid=向下取整(low+high)/2，对于任何一个结点，必有：右子树结点-左子树结点=0或1

自己过一遍顺序，1个元素，2个元素，。。。

折半查找的判定树一定是平衡二叉树

因此，元素个数为n时

[树高h=lceil log_2(n+1) ceil ]

计算完全二叉树也相同

满足二叉排序树的定义

失败节点：n+1个，等于成功结点的空链域数量

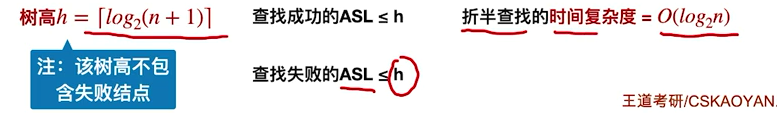
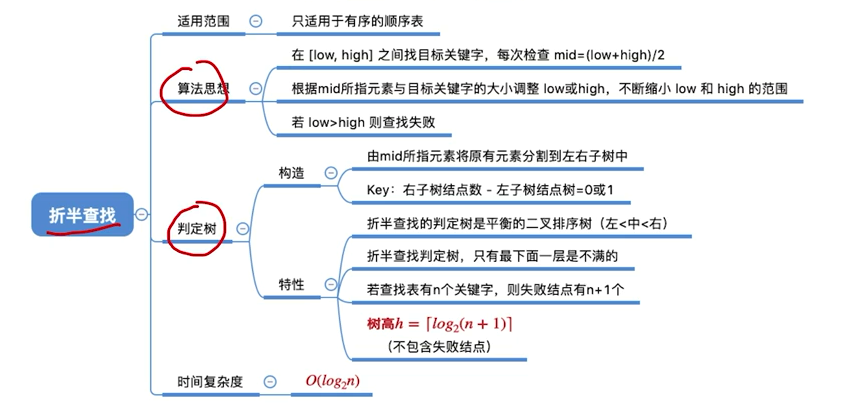
知识回顾

大部分情况下折半查找速度都比顺序查找快。但是不一定哦

从上去整，不一样哦，左边的比较多