2016-07-20 11:21:33
1受限玻尔兹曼机
梯度下降法(以及相关的L-BFGS算法等)在使用随机初始化权重的深度网络上效果不好的技术原因是:梯度会变得非常小。具体而言,当使用反向传播方法计算导数的时候,随着网络的深度的增加,反向传播的梯度(从输出层到网络的最初几层)的幅度值会急剧地减小。结果就造成了整体的损失函数相对于最初几层的权重的导数非常小。这样,当使用梯度下降法的时候,最初几层的权重变化非常缓慢,以至于它们不能够从样本中进行有效的学习。这种问题通常被称为“梯度的弥散”[4]。
与梯度弥散问题紧密相关的问题是:当神经网络中的最后几层含有足够数量神经元的时候,可能单独这几层就足以对有标签数据进行建模,而不用最初几层的帮助。因此,对所有层都使用随机初始化的方法训练得到的整个网络的性能将会与训练得到的浅层网络(仅由深度网络的最后几层组成的浅层网络)的性能相似。
梯度弥散一直是困扰着深度神经网络的发展,那么如何解决梯度弥散问题呢?多伦多大学的Geoff Hinton提出了设想:受限玻尔兹曼机(Restricted Boltzmann Machines, RBM)[1],即一类具有两层结构的、对称链接无自反馈的随机神经网络模型(一种特殊的马尔科夫随机场)。
如图1所示,一个RBM包含一个由随机的隐单元构成的隐藏层(一般是伯努利分布)和一个由随机的可见(观测)单元构成的可见(观测)层(一般是伯努利分布或高斯分布)。RBM可以表示成一个二分图模型,所有可见单元和隐单元之间存在连接,而隐单元两两之间和可见单元两两之间不存在连接,也就是层间全连接,层内无连接(这也是和玻尔兹曼机BM模型的区别,层间、层内全连接)。每一个可见层节点和隐藏层节点都有两种状态:处于激活状态时值为1,未被激活状态值为0。这里的0和1状态的意义是代表了模型会选取哪些节点来使用,处于激活状态的节点被使用,未处于激活状态的节点未被使用。节点的激活概率由可见层和隐藏层节点的分布函数计算。
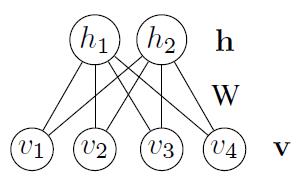
图1 受限玻尔兹曼机
一个RBM中,v表示所有可见单元,h表示所有隐单元。要想确定该模型,只要能够得到模型三个参数 ![]() 即可。分别是权重矩阵W,可见层单元偏置A,隐藏层单元偏置B。假设一个RBM有n个可见单元和m个隐单元,用
即可。分别是权重矩阵W,可见层单元偏置A,隐藏层单元偏置B。假设一个RBM有n个可见单元和m个隐单元,用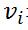 表示第i个可见单元,
表示第i个可见单元,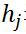 表示第j个隐单元,它的参数形式为:
表示第j个隐单元,它的参数形式为:
![]() :
: 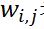 表示第i个可见单元和第j个隐单元之间的权值。
表示第i个可见单元和第j个隐单元之间的权值。
![]() :
:  表示第i个可见单元的偏置阈值。
表示第i个可见单元的偏置阈值。
![]() :
: 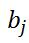 表示第j个隐单元的偏置阈值。
表示第j个隐单元的偏置阈值。
对于一组给定状态下的(v, h)值,假设可见层单元和隐藏层单元均服从伯努利分布,RBM的能量公式是:
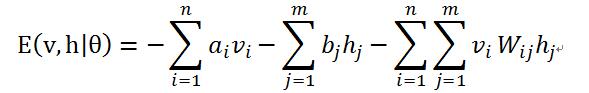
其中,令![]() 是RBM模型的参数(均为实数),能量函数表示在每一个可见节点的取值和每一个隐藏层节点的取值之间都存在一个能量值。
是RBM模型的参数(均为实数),能量函数表示在每一个可见节点的取值和每一个隐藏层节点的取值之间都存在一个能量值。
对该能量函数指数化和正则化后可以得到可见层节点集合和隐藏层节点集合分别处于某一种状态下(v, h)联合概率分布公式:
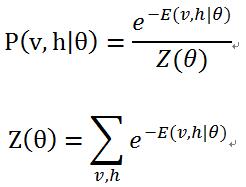
其中,![]() 为归一化因子或配分函数(partition function),表示对可见层和隐藏层节点集合的所有可能状态的(能量指数)求和。
为归一化因子或配分函数(partition function),表示对可见层和隐藏层节点集合的所有可能状态的(能量指数)求和。
对于参数的求解往往采用似然函数求导的方法。已知联合概率分布![]() ,通过对隐藏层节点集合的所有状态求和,可以得到可见层节点集合的边缘分布
,通过对隐藏层节点集合的所有状态求和,可以得到可见层节点集合的边缘分布![]() :
:
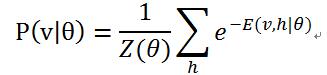
边缘分布表示的是可见层节点集合处于某一种状态分布下的概率,边缘分布往往被称为似然函数(如何对模型参数求解在下面章节阐述)。
由于RBM模型的特殊的层间连接、层内无连接的结构,它具有以下重要性质:
1)在给定可见单元的状态时,各隐藏层单元的激活状态之间是条件独立的。此时,第j个隐单元的激活概率为:
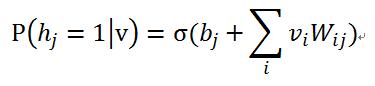
2)相应的,当给定隐单元的状态时,可见单元的激活概率同样是条件独立的: 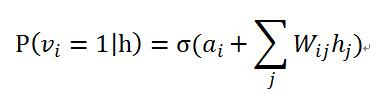
其中,![]() 是sigmoid函数,其函数曲线如图2所示:
是sigmoid函数,其函数曲线如图2所示:
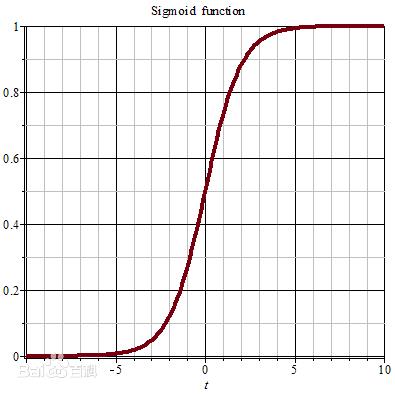
图2 Sigmoid函数
采用该函数用作每一层节点的激活概率公式的原因是:sigmoid函数的定义域是 ![]() ,值域处于(0,1)之间。也就是说,无论模型的可见层输入节点数据处于一个多大的范围内,都可以通过sigmoid函数求得它相应的函数值,即节点的激活概率值。
,值域处于(0,1)之间。也就是说,无论模型的可见层输入节点数据处于一个多大的范围内,都可以通过sigmoid函数求得它相应的函数值,即节点的激活概率值。
2模型参数求解
在给定一个训练样本后,训练一个RBM的意义在于调整模型的参数,以拟合给定的训练样本,使得在该参数下RBM表示的可见层节点概率分布尽可能的与训练数据相符合。
对于该模型需要确定两部分。一是如果想确定这个模型,首先是要知道可见层和隐藏层节点个数,可见层节点个数即为输入的数据维数,隐藏层节点个数在一些研究领域中是和可见层节点个数有关的,如用卷积受限玻尔兹曼机处理图像数据,在这里不多分析。但多数情况下,隐藏层节点个数需要根据使用而定或者是在参数一定的情况下,使得模型能量最小时的隐藏层节点个数。
其次,要想确定这个模型还得要知道模型的三个参数![]() ,下面就围绕着参数的求解进行分析。
,下面就围绕着参数的求解进行分析。
上面已经提到了,参数求解用到了似然函数的对数对参数求导。由于从![]() 可知,能量E和概率P是成反比的关系,所以通过最大化P,才能使能量值E最小。最大化似然函数常用的方法是梯度上升法,梯度上升法是指对参数进行修改按照以下公式:
可知,能量E和概率P是成反比的关系,所以通过最大化P,才能使能量值E最小。最大化似然函数常用的方法是梯度上升法,梯度上升法是指对参数进行修改按照以下公式:
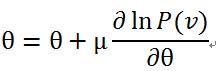
通过求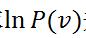 关于
关于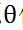 的导数,即
的导数,即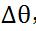 ,然后对原
,然后对原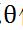 值进行修改。如此迭代使似然函数P最大,从而使能量E最小。
值进行修改。如此迭代使似然函数P最大,从而使能量E最小。
对数似然函数对参数求导分析:
首先是对数似然函数的格式: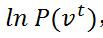 ,
, 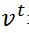 表示模型的输入数据。
表示模型的输入数据。
然后对![]() 里的参数分别进行求导,详细的推导过程就不写了:
里的参数分别进行求导,详细的推导过程就不写了:

由于上面三式的第二项中都含有![]() ,
, ![]() 中仍然含有参数,所以它是式中求不出来的。所以,有很多人就提出了一些通过采样逼近的方法来求每一个式子中的第二项。
中仍然含有参数,所以它是式中求不出来的。所以,有很多人就提出了一些通过采样逼近的方法来求每一个式子中的第二项。
3模型训练算法
3.1 Gibbs采样算法
因为在上一章节末尾讲对参数的求导中仍然存在不可求项![]() ,
, ![]() 表示可见层节点的联合概率。所以,要想得到
表示可见层节点的联合概率。所以,要想得到![]() 的值,就得要逼近它,求它的近似值。
的值,就得要逼近它,求它的近似值。
Gibbs采样的思想是虽然不知道一个样本数据![]() 的联合概率P(x),但是知道样本中每一个数据的条件概率
的联合概率P(x),但是知道样本中每一个数据的条件概率![]() (假设每一个变量都服从一种概率分布),则我可以先求出每一个数据的条件概率值,得到x的任一状态
(假设每一个变量都服从一种概率分布),则我可以先求出每一个数据的条件概率值,得到x的任一状态![]() 。然后,我用条件概率公式迭代对每一个数据求条件概率。最终,迭代k次的时候,x的某一状态
。然后,我用条件概率公式迭代对每一个数据求条件概率。最终,迭代k次的时候,x的某一状态 ![]() 将收敛于x的联合概率分布P(x)。
将收敛于x的联合概率分布P(x)。
对于RBM来讲,则执行过程如图3所示:
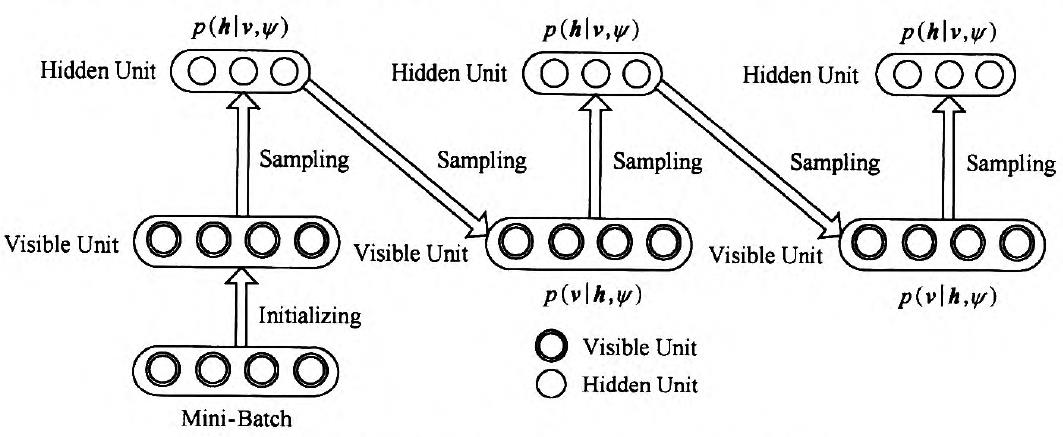
图3 Gibbs采样过程
求解过程是:假设给我一个训练样本v0,根据公式![]() 求 h0中每个节点的条件概率,再根据公式
求 h0中每个节点的条件概率,再根据公式![]() 求v1 中每个节点的条件概率,然后依次迭代,直到执行K步(K足够大),此时
求v1 中每个节点的条件概率,然后依次迭代,直到执行K步(K足够大),此时 ![]() 的概率将收敛于P(v)的概率。如下所示:
的概率将收敛于P(v)的概率。如下所示:

3.2 CD-k算法
CD算法是需要k次(k=1)Gibbs采样对可见层节点进行重构得到可见层节点的概率分布。其思想是:假设给模型一个样本v0,通过![]() 求所有隐藏层节点的概率值,然后每一个概率值和随机数进行比较得到每一个隐藏层节点的状态,然后通过公式
求所有隐藏层节点的概率值,然后每一个概率值和随机数进行比较得到每一个隐藏层节点的状态,然后通过公式![]() 求每一个可见层节点的概率值,再由
求每一个可见层节点的概率值,再由![]()
求每一个隐藏层节点的概率值。最后参数梯度的计算公式变为:

其中,μ是学习率,data和recon分别表示训练数据的概率分布和重构后的概率分布。
通过以上方法都可以求出参数的梯度来,由每一个参数的梯度对原参数值进行修改来使模型的能量减小。

图4 CD算法伪代码
4模型的评估
对于模型的评估,一般程序中并不会去真的计算当模型训练好时的模型能量E,而是采用近似的方法来对模型进行评估。
常用的近似方法是重构误差,所谓重构误差是指以训练样本作为初始状态,经过RBM模型的分布进行一次Gibbs采样后与原数据的差异值。具体解释如下:

对于一个给定的样本![]() ,通过公式
,通过公式![]() 对所有隐藏层节点的条件概率进行采样,再通过公式 对所有可见层节点的条件概率进行采样,最后由样本值和采样出的可见层概率值做差取绝对值,作为该模型的评估。重构误差能够在一定程度上反映RBM对训练数据的似然度。
对所有隐藏层节点的条件概率进行采样,再通过公式 对所有可见层节点的条件概率进行采样,最后由样本值和采样出的可见层概率值做差取绝对值,作为该模型的评估。重构误差能够在一定程度上反映RBM对训练数据的似然度。
5节点状态如何确定
对于每一层节点状态(0 or 1)的确定是采用与随机数(在0到1之间)进行比较的方法,如果节点被激活的概率值大于一个随机产生的数,则认为该节点被激活。原因是:给定可见层节点v时,隐藏层第j个节点状态为1的激活概率![]() 。这时,在区间[0,1]上产生一个随机数
。这时,在区间[0,1]上产生一个随机数![]() 落在子区间
落在子区间![]() 的概率也是
的概率也是![]() ,既然两个事件的概率是相等的,若随机数
,既然两个事件的概率是相等的,若随机数![]() 落在子区间
落在子区间![]() ,则认为第j个节点的状态为1,否则为0。
,则认为第j个节点的状态为1,否则为0。
如下:对于隐藏层节点的激活状态

同理,对于可见层节点的激活状态

总结:受限玻尔兹曼机网络模型的目的就是最大可能的拟合输入数据,即最大化![]() 。Hinton提出的一种快速训练算法,即contrastive divergence(对比散度CD-k)算法。
。Hinton提出的一种快速训练算法,即contrastive divergence(对比散度CD-k)算法。
该算法需要迭代k次,就可以获得模型对输入数据的估计,而通常k取1。CD算法在开始是用训练数据去初始化可见层,然后用条件分布计算隐藏层;然后,再根据隐藏层状态,同样,用条件分布计算可见层。这样产生的结果就是对训练数据的一个重构。根据CD算法可得模型对网络权值的梯度:
![]()
其中,μ是学习率, ![]() 是样本数据的期望,
是样本数据的期望, ![]() 是重构后可见层数据的期望。
是重构后可见层数据的期望。
6深度置信网络
本节讨论RBM如何堆叠组成一个深度置信网络(Deep Belief Network, DBN),从而作为DBN预训练的基础模型。在进行细节探究之前,我们需要首先知道,由Hinton和Salakhutdinov在文章[2]提出的这种预训练过程是一种无监督的逐层预训练的通用技术,也就是说,不是只有RBM可以堆叠成一个深度生成式(或判别式)网络,其他类型的网络也可以使用相同的方法来生成网络,比如Bengio等人在文献[3]中提出的自动编码器(autoencoder)的变形。
图5描述了一个逐层训练的例子,将一定数目的RBM堆叠成一个DBN,然后从底向上逐层预训练。堆叠过程如下:训练一个高斯-伯努利RBM(对于语音应用使用的连续特征)或伯努利-伯努利RBM(对于正态分布或二项分布特征应用,如黑白图像或编码后的文本)后,将隐单元的激活概率(activation probabilities)作为下一层伯努利-伯努利RBM的输入数据。第二层伯努利-伯努利RBM的激活概率作为第三层伯努利-伯努利RBM的可见层输入数居,以后各层以此类推。关于这种有效的逐层贪婪学习策略的理论依据由文献[2]给出。已经表明,上述的贪婪过程达到了近似的最大似然学习。这个学习过程是无监督的,所以不需要标签信息。
当应用到分类任务时,生成式预训练可以和其他算法结合使用,典型的是判别式方法,他通过有效地调整所有权值来改善网络的性能。判别式精调(fine-tune)通常是在现有网络的最后一层上在增加一层节点,用来表示想要的输出或者训练数据提供的标签,它与标准的前馈神经网络(feed-forward neural network)一样,可以使用反向传播算法(back-propagation algorithm)来调整或精调网络的权值。DBN最后一层即标签层的内容,根据不同的任务和应用来确定。
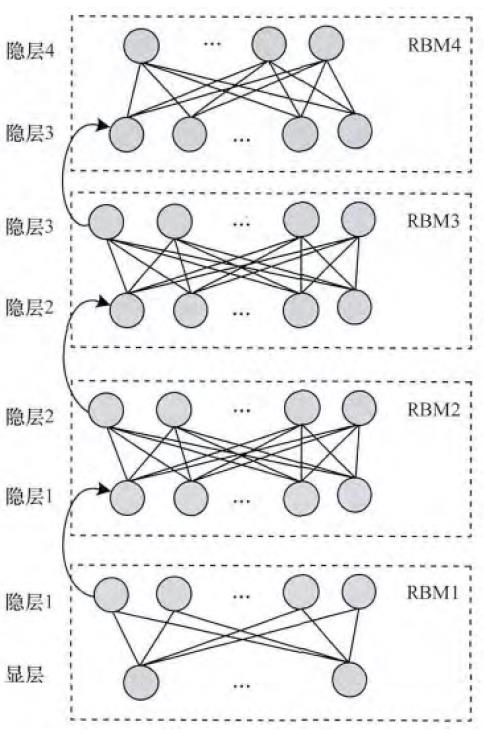
图5 DBN逐层预训练示意图
上述生成式预训练应用在音素和语音识别中,要比随机初始化网络的效果要好。研究已经表明其他种类的预训练策略的有效性。比如,在执行逐层贪婪训练时,可以在每一层的生成损失函数中增加一项判别项。如果不适用生成式预训练,只使用随机梯度下降方法来对随机初始化DBN进行判别式训练,研究结果表明,当非常仔细的选取初始权值并且谨慎的选取适合于随机梯度下降的“迷你批量”(mini-batch)的大小(例如,随着训练轮数增加大小),也将会获得很好的效果。“迷你批量”用于在收敛速度和噪声梯度之间进行折中。同时,在建立“迷你批量”时,对数据进行充分的随机化也是至关重要的。另外,很重要的一个发现是:从一个只含有一层的浅层神经网络开始学习一个DBN是非常有效的。当折中方法用于训练区分式模型时(使用提前结束训练的策略以防止过拟合的出现),在第一个隐藏层和标签的softmax输出层之间插入第二个隐藏层,然后对整个网络应用反向传播来微调网络的权值。这种判别式预训练在实践中取得了比较好的效果,特别是在有大量的训练数据的情况下效果较好。当训练数据不断增多时,即使不使用上述预训练,一些特别设计的随机初始化方法也能够取得很好的效果。
参考文献
[1] Hinton G. A practical guide to training restricted Boltzmann machines[J]. Momentum, 2010, 9(1): 926.
[2] Hinton G E, Osindero S, Teh Y W. A fast learning algorithm for deep belief nets[J]. Neural computation, 2006, 18(7): 1527-1554.
[3] Bengio Y, Lamblin P, Popovici D, et al. Greedy layer-wise training of deep networks[J]. Advances in neural information processing systems, 2007, 19: 153.