这里不讨论数学原理,只说明其实现和传输过程。
我们先假定一个数据的发送方和一个数据的接收方(就叫小红和小明好了!)
发送方小红拥有一对密钥:一个公钥和一个私钥。
接收方小明也同样拥有一对密钥:一个公钥和私钥。
注意:这四把钥匙(密码)各不相同!
公钥的概念:公钥是可以在网络上传输的,也就是说接收发送双方都可以知道彼此的公钥,当然,如果你用网络嗅探等技术,也可以在网络上嗅探的公钥的内容,但你仅有公钥是无法解密文件的。
私钥的概念:私钥是用户各自私有的,不会在网络中传输(也就是说不需要接收发送双方彼此交换此密钥),这就保证了此密码的安全性,黑客无法在网络中嗅探到该密钥,而是被严格的储存在用户自己的主机中。
公钥和私钥的关系:公钥加密的数据只有私钥可以解锁,私钥加密的数据只有公钥能解锁,而两者都无法自己解锁自己!这一点是保证数据无法被窃取的关键!而公钥和私钥的唯一区别也接就是公钥会互相交换在网络上传输,而私钥自己保留不在网络上传输。
下面介绍数据加密传出过程(如下图):
想象以下场景:
发送方小红要向接收方小明发送一封情书(好吧,为了配合下面的图我只能编个女追男的故事,让广大吊丝意淫下!),但是小红呢,女孩子嘛,比较害羞,怕某些别有用心的人偷看到他写给心上人的悄悄话,就利用了加密技术,让网络上无聊的人们无法偷窥到它的情书。
第一步:小红用自己的私钥给情书上了第一道锁,这个私钥只有她自己知道。
第二步:其实两人之前相互了解过(通信过),这个时候已经都拥有的对方的公钥,所以小红又在第一步的基础上用小明的公钥给情书加了第二把锁。
第三步:这个时候小红这边就已经把情书加密好了,她很满意,因为已经万无一失了!她把加了两把锁的情书发到网络上传送给小明,这个时候网络上的黑客们也许已经在小红和小明初次幽会并交换公钥的时候窃取到了两人的公钥。但请想想小红的加锁过程,最外面一道锁(第二道锁)是用小明的公钥加密的,也就是说要用小明的私钥来解密才可以打开,但黑客最多只能拥有两人的公钥,而无法获得小明的私钥,这就有效的避免的数据被窃取,即使黑客截获了情书,也只能看到一堆杂乱无章的乱码,而无法真正得知情书的内容。
第四步:小明顺利的接收到了小红的情书,利用自己的私钥,成功解开的外层的锁。(外层的锁是小红用小明的公钥锁的!)
第五步:小明又拿出了小红的公钥,解开了情书内层的锁。这时候就可确定情书确实是小红发的,而不是其他人伪造来忽悠自己的。(内层的锁是小红用自己的私钥锁的!)
最终,小明成功的看到了小红的情书,心中暗爽:吊到妹纸的感觉真好!
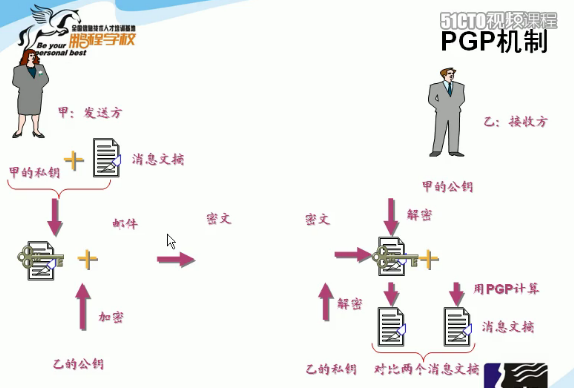
注:整个过程中利用两把锁将数据的传输过程严格加密,数据在传输过程中无法被解密,除非黑客入侵了接收方(小明)的电脑,窃取了他的私钥。所以,此种方法可以保证在传输过程中是严格保密的,即使收发双方交换的公钥被嗅探到也无法揭秘。当然,没有绝对的安全,如前面所说,直接被入侵了电脑那就无存在什么秘密了~
#1楼 2014-05-02 23:32 灬达 假如说小红只用小明的公钥加密,那黑客拿到数据也解不开,为什么要加两道锁呢? 支持(0)反对(0) 回复引用 #2楼[楼主] 2014-05-03 12:31 DarkSir @ 灬达 不好意思,写的不够细,等有时间写个详细且在生产环境中应用的流程!小红拿私钥上第一道锁叫做“签名”,是为了保证数据来源的真是性。也就是说,如果数据只拿接受放的公钥上锁,黑客虽然解不开,但却可以伪装成发送方向小明(接收方)发送数据,而接收方小明因数据没有发送方的私钥上锁,无法确定发送方的身份,所以如果一道锁的话,黑客还是有机可乘! 支持(0)反对(0) 回复引用 #3楼 2014-05-03 12:44 灬达 @ DarkSir 也就是说第一道锁保证了数据的安全性,第二道锁保证了数据来源的真实性,可以这样理解吧 支持(0)反对(0) 回复引用 #4楼[楼主] 2014-05-03 12:47 DarkSir @ 灬达 对,一道保证只有要接收方才能看,一道保证必须是发送方发的。两边都要确认!