hiho #1196 : 高斯消元·二

#1196 : 高斯消元·二

时间限制:10000ms

单点时限:1000ms

内存限制:256MB

描述

在上一回中，小Hi和小Ho趁着便利店打折，买了一大堆零食。当他们结账后，看到便利店门口还有其他的活动。

店主：买了东西还可以参加游戏活动哦，如果能够完成游戏还有额外的奖品。

小Hi和小Ho赶紧凑了过去。

店主放了一块游戏板在店门口，有5行6列格子。左上角为坐标(1,1)。一部分格子是亮着的，另一部分是暗着的。

 当按下某一个格子时，它和上下左右4个格子的状态就会改变。原来亮着的格子变成暗的，原来暗的格子会变亮。比如下图中按下标记有红叉的格子后，绿色虚线区域内的格子状态都会改变：

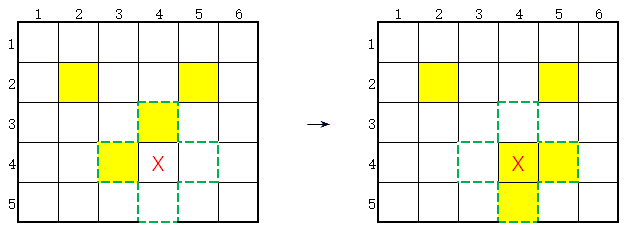
店主给出初始的状态，参加游戏的人员需要通过按下某些格子，让游戏板上所有的灯都亮起来就可以赢得奖品。

小Ho：这不就是开关灯问题么，看我来解决它！

本题改编自ACMICPC Greater New York 2002 EXTENDED LIGHTS OUT

   

提示：异或方程组

 

输入

第1..5行：1个长度为6的字符串，表示该行的格子状态，1表示该格子是亮着的，0表示该格子是暗的。

保证一定存在解，且一定存在暗着的格子。

输出

需要按下的格子数量k，表示按下这k个位置后就可以将整个游戏板所有的格子都点亮。

接下来k行，每行一个坐标(x,y)，表示需要按下格子(x,y)。x坐标较小的先输出，若x相同，则先输出y坐标较小的。

样例输入

001111
011111
111111
111110 
111100

样例输出

2
1 1
5 6

思路：高斯求异或方程组的解；kuangbin板子

#pragma comment(linker, "/STACK:1024000000,1024000000")
#include<iostream>
#include<cstdio>
#include<cmath>
#include<string>
#include<queue>
#include<algorithm>
#include<stack>
#include<cstring>
#include<vector>
#include<list>
#include<set>
#include<map>
#include<stdlib.h>
#include<time.h>
using namespace std;
#define ll long long
#define pi (4*atan(1.0))
#define eps 1e-6
#define bug(x)  cout<<"bug"<<x<<endl;
const int N=1e3+10,M=1e6+10,inf=1e9+10;
const ll INF=5e17+10,mod=1e9+7;

//对2取模的01方程组
const int MAXN = 40;
//有equ个方程，var个变元。增广矩阵行数为equ,列数为var+1,分别为0到var
int a[MAXN][MAXN]; //增广矩阵
int x[MAXN]; //解集
int free_x[MAXN];//用来存储自由变元（多解枚举自由变元可以使用）
int free_num;//自由变元的个数

//返回值为-1表示无解，为0是唯一解，否则返回自由变元个数
int Gauss(int var,int equ)
{
    int max_r,col,k;
    free_num = 0;
    for(k = 0, col = 0 ; k < equ && col < var ; k++, col++)
    {
        max_r = k;
        for(int i = k+1;i < equ;i++)
        {
            if(abs(a[i][col]) > abs(a[max_r][col]))
                max_r = i;
        }
        if(a[max_r][col] == 0)
        {
            k--;
            free_x[free_num++] = col;//这个是自由变元
            continue;
        }
        if(max_r != k)
        {
            for(int j = col; j < var+1; j++)
                swap(a[k][j],a[max_r][j]);
        }
        for(int i = k+1;i < equ;i++)
        {
            if(a[i][col] != 0)
            {
                for(int j = col;j < var+1;j++)
                    a[i][j] ^= a[k][j];
            }
        }
    }
    for(int i = k;i < equ;i++)
        if(a[i][col] != 0)
            return -1;//无解
    if(k < var) return var-k;//自由变元个数
    //唯一解，回代
    for(int i = var-1; i >= 0;i--)
    {
        x[i] = a[i][var];
        for(int j = i+1;j < var;j++)
            x[i] ^= (a[i][j] && x[j]);
    }
    return 0;
}
int getpos(int x,int y)
{
    return (x-1)*6+y;
}
char s[MAXN][MAXN];
int check(int x,int y)
{
    if(x<=0||x>5||y<=0||y>6)
        return 0;
    return 1;
}
int xx[5]={1,0,-1,0};
int yy[5]={0,-1,0,1};
void init()
{
    for(int i=1;i<=5;i++)
    {
        for(int j=1;j<=6;j++)
        {
            a[getpos(i,j)-1][30]=(s[i][j]-'0')^1;
            a[getpos(i,j)-1][getpos(i,j)-1]=1;
            for(int k=0;k<4;k++)
            {
                int x=i+xx[k];
                int y=j+yy[k];
                if(check(x,y))a[getpos(i,j)-1][getpos(x,y)-1]=1;
            }
        }
    }
}
int main()
{
    memset(x,0,sizeof(x));
    memset(a,0,sizeof(a));
    for(int i=1;i<=5;i++)
        scanf("%s",s[i]+1);
    init();
    int mmp=Gauss(30,30);
    int ans=0;
    for(int i=0;i<30;i++)
    {
        if(x[i])ans++;
    }
    printf("%d
",ans);
    for(int i=0;i<30;i++)
        if(x[i]) printf("%d %d
",i/6+1,i%6+1);
    return 0;
}

/*
001111
011111
111111
111110
111100
*/