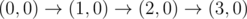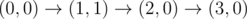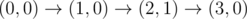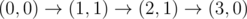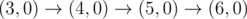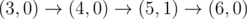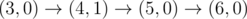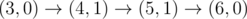Codeforces Round #420 (Div. 2) E. Okabe and El Psy Kongroo 矩阵快速幂优化dp

E. Okabe and El Psy Kongroo

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Okabe likes to take walks but knows that spies from the Organization could be anywhere; that's why he wants to know how many different walks he can take in his city safely. Okabe's city can be represented as all points (x, y) such that x and y are non-negative. Okabe starts at the origin (point (0, 0)), and needs to reach the point (k, 0). If Okabe is currently at the point (x, y), in one step he can go to (x + 1, y + 1), (x + 1, y), or (x + 1, y - 1).

Additionally, there are n horizontal line segments, the i-th of which goes from x = a_i to x = b_i inclusive, and is at y = c_i. It is guaranteed that a₁ = 0, a_n ≤ k ≤ b_n, and a_i = b_i - 1 for 2 ≤ i ≤ n. The i-th line segment forces Okabe to walk with y-value in the range 0 ≤ y ≤ c_i when his x value satisfies a_i ≤ x ≤ b_i, or else he might be spied on. This also means he is required to be under two line segments when one segment ends and another begins.

Okabe now wants to know how many walks there are from the origin to the point (k, 0) satisfying these conditions, modulo 10⁹ + 7.

Input

The first line of input contains the integers n and k (1 ≤ n ≤ 100, 1 ≤ k ≤ 10¹⁸) — the number of segments and the destination x coordinate.

The next n lines contain three space-separated integers a_i, b_i, and c_i (0 ≤ a_i < b_i ≤ 10¹⁸, 0 ≤ c_i ≤ 15) — the left and right ends of a segment, and its y coordinate.

It is guaranteed that a₁ = 0, a_n ≤ k ≤ b_n, and a_i = b_i - 1 for 2 ≤ i ≤ n.

Output

Print the number of walks satisfying the conditions, modulo 1000000007 (10⁹ + 7).

Examples

Input

1 3
0 3 3

Output

4

Input

2 6
0 3 0
3 10 2

Output

4

Note

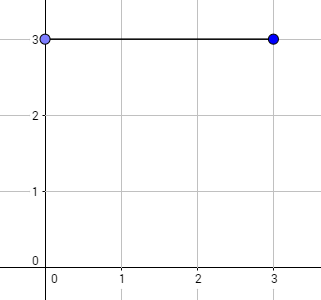
The graph above corresponds to sample 1. The possible walks are:

• 
• 
• 
• 

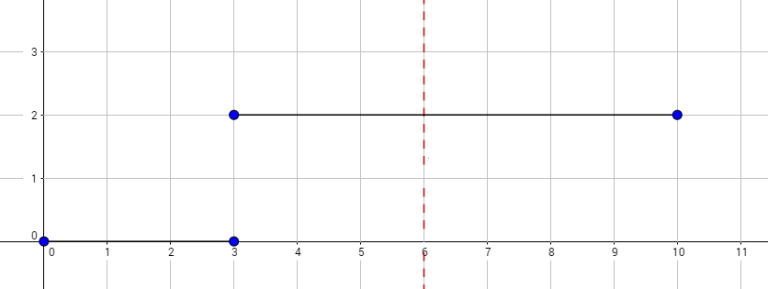
The graph above corresponds to sample 2. There is only one walk for Okabe to reach (3, 0). After this, the possible walks are:

• 
• 
• 
• 

#pragma comment(linker, "/STACK:1024000000,1024000000")
#include<iostream>
#include<cstdio>
#include<cmath>
#include<string>
#include<queue>
#include<algorithm>
#include<stack>
#include<cstring>
#include<vector>
#include<list>
#include<set>
#include<map>
#include<bitset>
#include<time.h>
using namespace std;
#define LL long long
#define pi (4*atan(1.0))
#define eps 1e-4
#define bug(x)  cout<<"bug"<<x<<endl;
const int N=3e5+10,M=4e6+10,inf=2147483647,mod=1e9+7;
const LL INF=1e18+10,MOD=1e9+7;

struct Matrix
{
    LL a[20][20];
    Matrix()
    {
        memset(a,0,sizeof(a));
    }
    void init()
    {
        for(int i=0;i<18;i++)
            for(int j=0;j<18;j++)
                a[i][j]=(i==j);
    }
    Matrix operator + (const Matrix &B)const
    {
        Matrix C;
        for(int i=0;i<18;i++)
            for(int j=0;j<18;j++)
                C.a[i][j]=(a[i][j]+B.a[i][j])%MOD;
        return C;
    }
    Matrix operator * (const Matrix &B)const
    {
        Matrix C;
        for(int i=0;i<18;i++)
            for(int k=0;k<18;k++)
                for(int j=0;j<18;j++)
                    C.a[i][j]=(C.a[i][j]+1LL*a[i][k]*B.a[k][j])%MOD;
        return C;
    }
    Matrix operator ^ (const LL &t)const
    {
        Matrix A=(*this),res;
        res.init();
        LL p=t;
        while(p)
        {
            if(p&1)res=res*A;
            A=A*A;
            p>>=1;
        }
        return res;
    }
};
map<pair<LL,int> ,LL >dp;
LL a[N],b[N];int c[N];
Matrix Gbase(int n)
{
    Matrix a;
    a.init();
    for(int i=0;i<=n;i++)
    {
        if(i-1>=0)a.a[i-1][i]=1;
        a.a[i][i]=1;
        if(i+1<=n)a.a[i+1][i]=1;
    }
    return a;
}
Matrix Gpre(LL x,int n)
{
    Matrix a;
    a.init();
    for(int i=0;i<=n;i++)
        a.a[0][i]=dp[make_pair(x,i)];
    return a;
}
int main()
{
    int n;
    LL k;
    scanf("%d%lld",&n,&k);
    for(int i=1;i<=n;i++)
        scanf("%lld%lld%d",&a[i],&b[i],&c[i]);
    dp[make_pair(0,0)]=1;
    for(int i=1;i<=n;i++)
    {
        Matrix base=Gbase(c[i]);
        Matrix pre=Gpre(a[i],c[i]);
        LL l=a[i],r=min(b[i],k);
        base=base^(r-l);
        Matrix ans=pre*base;
        for(int j=0;j<=c[i];j++)
            dp[make_pair(r,j)]=ans.a[0][j];
        if(b[i]>=k)break;
    }
    printf("%lld
",dp[make_pair(k,0)]);
    return 0;
}