DP基础练习(4.21)

数塔

Description 

在讲述DP算法的时候，一个经典的例子就是数塔问题，它是这样描述的：

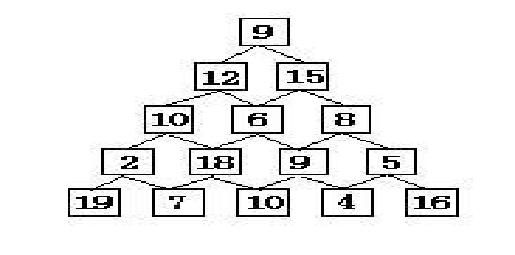
有如下所示的数塔，要求从顶层走到底层，若每一步只能走到相邻的结点，则经过的结点的数字之和最大是多少？

Input

 

输入数据首先包括一个整数C,表示测试实例的个数，每个测试实例的第一行是一个整数N(1 <= N <= 100)，表示数塔的高度，接下来用N行数字表示数塔，其中第i行有个i个整数，且所有的整数均在区间[0,99]内。

Output

 

对于每个测试实例，输出可能得到的最大和，每个实例的输出占一行。

 Sample Input 1

1
5
7
3 8
8 1 0 
2 7 4 4
4 5 2 6 5

Sample Output 1

30

#include <cstdio>
#include <algorithm> 

using namespace std;

int main()
{
    int c;
    scanf("%d",&c);
    while(c--)
    {
        int a[101][101]={0};
        int dp[101][101]={0};
        int n;
        scanf("%d",&n);
        for(int i=1;i<=n;i++)
        {
            for(int j=1;j<=i;j++)
            {
                scanf("%d",&a[i][j]);
            }
        }
        for(int i=1;i<=n;i++)
        {
            dp[n][i]=a[n][i];
        }
        for(int i=n-1;i>=1;i--)
        {
            for(int j=1;j<=i;j++)
            {
                dp[i][j]=max(dp[i+1][j],dp[i+1][j+1])+a[i][j];
            }
        }
        printf("%d
",dp[1][1]);
    } 
    return 0;
}

音量调节

Description

一个吉他手准备参加一场演出。他不喜欢在演出时始终使用同一个音量，所以他决定每一首歌之前他都要改变一次音量。在演出开始之前，他已经做好了一个列表，里面写着在每首歌开始之前他想要改变的音量是多少。每一次改变音量，他可以选择调高也可以调低。
音量用一个整数描述。输入文件中给定整数beginLevel，代表吉他刚开始的音量，以及整数maxLevel，代表吉他的最大音量。音量不能小于0也不能大于maxLevel。输入文件中还给定了n个整数c1,c2,c3…..cn，表示在第i首歌开始之前吉他手想要改变的音量是多少。
吉他手想以最大的音量演奏最后一首歌，你的任务是找到这个最大音量是多少。

Input

第一行依次为三个整数：n, beginLevel, maxlevel。
第二行依次为n个整数：c1,c2,c3…..cn。

Output

输出演奏最后一首歌的最大音量。如果吉他手无法避免音量低于0或者高于maxLevel，输出-1。

Sample Input

3 5 10 
5 3 7

Sample Output

10

HINT

1<=N<=50,1<=Ci<=Maxlevel 1<=maxlevel<=1000

0<=beginlevel<=maxlevel

Source

一开始便开始想用f[i]表示前i个物品能够得到的最大的音量，以为和装箱问题一样。于是借用一下强大的搜索引擎，发现一种叫布尔型dp，就是用f[i][j]表示前i个物品在音量为j时可行；记住这种表示方式；

#include <iostream>
#include <cstring> 
#include <algorithm> 

using namespace std;

int a[1010];
bool dp[55][1010];

int main()
{
    int n,initial,maxl;
    cin>>n>>initial>>maxl;
    for(int i=1;i<=n;i++)
    {
        cin>>a[i];
    }
    memset(dp,false,sizeof(dp));
    dp[0][initial]=true;
    for(int i=1;i<=n;i++)
    {
        for(int j=0;j<=maxl;j++)
        {
            //dp[i][j]是第i次调节可以获得的音量j 
            dp[i][j]=((j+a[i]<=maxl)&&dp[i-1][j+a[i]])||((j-a[i]>=0)&&dp[i-1][j-a[i]]);
            //j+a[i]<=maxl和 j-a[i]>=0判断是否超出dp[]的范围
            //dp[i-1][j+a[i]]为真说明第i次调节后的j可以是第i-1次的某个音量减去a[i]得到 
            //dp[i-1][j-a[i]]为真说明第i次调节后的j可以是第i-1次的某个音量加上a[i]得到 
        }
    }
    for(int i=maxl;i>=0;i--)
    {
        if(dp[n][i])
        {
            cout<<i<<endl;
            return 0;
        }
    }
    cout<<-1<<endl;    
    return 0;
}

消失之物

Description
ftiasch 有 N 个物品, 体积分别是 W1, W2, ..., WN。 由于她的疏忽, 第 i 个物品丢失了。 “要使用剩下的 N - 1 物品装满容积为 x 的背包，有几种方法呢？” -- 这是经典的问题了。她把答案记为 Count(i, x) ，想要得到所有1 <= i <= N, 1 <= x <= M的 Count(i, x) 表格。

 

Input
 
第1行：两个整数 N (1 ≤ N ≤ 2 × 103) 和 M (1 ≤ M ≤ 2 × 103)，物品的数量和最大的容积。

第2行： N 个整数 W1, W2, ..., WN, 物品的体积。

Output
 
一个 N × M 的矩阵， Count(i, x)的末位数字。

Sample Input
3 2
1 1 2
Sample Output
11
11
21
HINT
如果物品3丢失的话，只有一种方法装满容量是2的背包，即选择物品1和物品2。

题解
先考虑不删除物品怎么做，其实就是一个背包，dp[i][j]=dp[i-1][j]+dp[i-1][j-w[i]];那么现在考虑少了物品i会减少几种方案，当x小于w[i]时，i物品一定不会被选上 g[i]=f[i] 当x大于等于w[i]时，i物品可能会被选上，直接求不选的情况比较困难。可以换个思路，设g[x]为不选当前物品的容量为x的方案数，用总方案数-选的方案数得到不选的方案数。总方案数及f[x]，不选的方案数可以想为先不选i再最后把i选上,即g[x-w[i]]。

#include<cstdio>
#include<algorithm>
#include<cstring>
#include<iostream>
using namespace std;
const int N=100010;
int f[N],g[N],w[N];
int n,m;
int main(){
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++) scanf("%d",&w[i]);
    
    f[0]=1;
    for(int i=1;i<=n;i++){
        for(int j=m;j>=w[i];j--)
        f[j]=(f[j]+f[j-w[i]])%10;
    }
    for(int i=1;i<=n;i++){
        for(int j=0;j<=m;j++){
            if(j<w[i]) g[j]=f[j];
            else g[j]=(f[j]-g[j-w[i]]+10)%10;
        }
        for(int j=1;j<=m;j++) printf("%d",g[j]);
        printf("
");
    }
    return 0;
}

分析

很明显是个01背包的dp,但是问题在于统计这个答案上。感觉和容斥原理略有关系？于是研读了一下黄学长的极妙的做法

首先，f[j]表示装满容积为j的背包的方案数 很明显，f[j]+=f[j-w[i]] (f[0]=1)

统计答案我们用c[i][j]表示

再枚举I,j

如果f[j]<w[i]，显然，装满容积j显然不可能用到第i个物品，所以c[i][j]=f[j]。

如果f[j]>=w[i],f[j]里就包括了选择了第i件物品的情况，那我们需要扣除掉这一部分。把扣除的这部分转换一下：

用第i件物品填满j ---> 用了其他物品填了j-w[i]，所以c[i][j]=f[j]-c[i][j-w[i]]

#include<bits/stdc++.h>
using namespace std;
#define N 2020
int n,m;
int f[N],w[N];
int    c[N][N];
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++)
        scanf("%d",&w[i]);
    f[0]=1;
    for(int i=1;i<=n;i++)
        for(int j=m;j>=w[i];j--)
            f[j]+=f[j-w[i]],f[j]%=10;
    for(int i=1;i<=n;i++)
    {
        c[i][0]=1;
        for(int j=1;j<=m;j++)
        {
            if(j>=w[i])c[i][j]=(f[j]-c[i][j-w[i]]+10)%10;
            else    c[i][j]=f[j];
            printf("%d",c[i][j]);
        }    
        printf("
");        
    }
    return 0;    
}

货币系统

在网友的国度中共有 n 种不同面额的货币，第 i 种货币的面额为 a[i]，你可以假设每一种货币都有无穷多张。为了方便，我们把货币种数为 n、面额数组为 a[1…n] 的货币系统记作 (n,a)。

在一个完善的货币系统中，每一个非负整数的金额 x 都应该可以被表示出，即对每一个非负整数 x，都存在 n 个非负整数 t[i] 满足 a[i]×t[i] 的和为 x。然而， 在网友的国度中，货币系统可能是不完善的，即可能存在金额 x 不能被该货币系统表示出。例如在货币系统 n=3, a=[2,5,9] 中，金额 1,3 就无法被表示出来。

两个货币系统 (n,a) 和 (m,b) 是等价的，当且仅当对于任意非负整数 x，它要么均可以被两个货币系统表出，要么不能被其中任何一个表出。

现在网友们打算简化一下货币系统。他们希望找到一个货币系统 (m,b)，满足 (m,b) 与原来的货币系统 (n,a) 等价，且 m 尽可能的小。他们希望你来协助完成这个艰巨的任务：找到最小的 m。

输入
输入文件的第一行包含一个整数 T，表示数据的组数。
接下来按照如下格式分别给出 T 组数据。 每组数据的第一行包含一个正整数 n。接下来一行包含 n 个由空格隔开的正整数 a[i]。

输出
输出文件共有 T 行，对于每组数据，输出一行一个正整数，表示所有与 (n,a) 等价的货币系统 (m,b) 中，最小的 m。

输入

2
4
3 19 10 6
5
11 29 13 19 17

输出

2
5

说明

在第一组数据中，货币系统(2, [3,10])和给出的货币系统(n, a)等价，并可以验证不存在m < 2的等价的货币系统，因此答案为2。
在第二组数据中，可以验证不存在m < n的等价的货币系统，因此答案为5。

备注:

1 <= T <= 20, 1 <= n <= 100, 1 <= a[i] <= 25000

解题思路
题目说的很长，其实题目的大意就是有 n nn 个数，然后让你找 m mm 个数使得这 m mm 个数与 n nn 个数的表示范围相同。那么我们来分析一下，首先相同的数字肯定是没有意义的，我们对原数组进行去重，然后我们用一个数组 vis[i] vis[i]vis[i] 表示数字 i ii 是否能够表示，如果 vis[i]=true vis[i]=truevis[i]=true 可以表示，否则不可以表示。那么我们就对于 n nn 个数中的每一个数字进行判断，第一个 a[0] a[0]a[0] 肯定不能表示，那么我们结果 ans++ ans++ans++， 然后把 a[0] a[0]a[0] 能够表示的数字 i ii 全标记为 vis[i]=true vis[i]=truevis[i]=true；那么在检查第 i ii 个数字，如果能够用已经标记的数字表示，那么说明这个数可以用 之前的数表示，答案不记录；否则答案记录，而且将已经能够表示的数字加上 a[i] a[i]a[i]，也进行标记 vis[j+a[i]]=true vis[j+a[i]]=truevis[j+a[i]]=true，直至循环完毕，输出 ans ansans 即可。

#include <iostream>
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <math.h>
#include <set>
#include <vector>
#include <algorithm>
#define pb push_back
#define mk make_pair
#define fi first
#define se second
using namespace std;
typedef pair<int, int> pii;
typedef long long LL;
typedef unsigned long long ULL;
const int MAXN = 25000+5;
int a[105];
bool vis[MAXN];
int main() {
    int T; cin>>T;
    while(T--) {
        int n; cin>>n;
        for(int i=0; i<n; i++) cin>>a[i];
        sort(a, a+n);
        n = unique(a, a+n)-a;
        memset(vis, false, sizeof vis);
        vis[0] = true;
        int ans = 0;
        for(int i=0; i<n; i++) {
            if(!vis[a[i]]) {
                ans++;
                for(int j=0; j<MAXN; j++) if(j+a[i]<=25000&&vis[j]) vis[j+a[i]] = true;
            }
        }
        cout<<ans<<endl;
    }
    return 0;
}

题解
首先我想弱弱地说一句，比赛的时候我并没有看懂这道题，也就是说没有思路说多了都是泪

但是我下来想了一下，这道题可以用背包来做

递推式（转移方程）为f[i]=max(f[i],f[i−money[j]]+1)

 f[i]表示i面值最多能被几张钱表示

f[i]=-inf表示有且只有它自己则f[i]=1

在开始之前初始化f[0]=0

就是这样~

#include<iostream>
#include<cstring>
using namespace std;
int a[500], n;
int ans;
int f[50000];
int main() {
    //freopen("money.in","r",stdin);
    //freopen("money.out","w",stdout);
    int T;
    cin >> T;
    for(int k = 1; k <= T; k++) {
        memset(f, -10000, sizeof f);
        ans = 0;
        cin >> n;
        for(int i=1; i<=n; i++)
            cin >> a[i];
        f[0] = 0;
        for(int i = 1; i <= n; i++) {
            for(int j = a[i]; j <= 30000; j++) {
                f[j] = max(f[j], f[j - a[i]] + 1);
            }
        }
        for(int i = 1; i <= n; i++)
            if(f[a[i]] == 1) {
                ans++;
            }
        cout << ans << endl;
    }
}
 

一个结论性的题目……吧。

首先手推一下，发现新货币系统中的最小值 m′ m&#x27;m
′
一定等于原来的货币系统中的最小值 m mm。如果大于，则新货币系统无法表达 m mm；如果小于，则原货币系统无法表达 m′ m&#x27;m
′
。

然后我们递归性地猜想：假如我去掉了这个最小值以及最小值能表达的数（因为新货币系统里面如果再有这些数就不够优秀了），那么再选择最小值是否也一定是最优的？
仿照上面的证明可以发现这个推论是正确的。

因此我们就可以得到我们的算法：
（1）找到原货币系统当前的最小值，加入新货币系统。
（2）在原货币系统中删除新货币系统能表达的数。
循环（1），（2）直到原货币系统没有任何数。

我们实现上可以不按这么写。我们可以从小到大枚举原货币系统中的数，判断它能否被新货币系统表达。能则跳过；不能则更新新货币系统。
判断以及更新可以用完全背包来做。

#include<cstdio>
#include<algorithm>
using namespace std;
const int MAXN = 100;
const int MAXM = 25000;
bool dp[MAXM + 5];
int a[MAXN + 5];
void solve() {
    int n, m = 0, lim = 0;
    scanf("%d", &n);
    for(int i=1;i<=n;i++) {
        scanf("%d", &a[i]);
        lim = max(lim, a[i]);
    }
    for(int i=0;i<=lim;i++)
        dp[i] = false;
    sort(a+1, a+n+1); dp[0] = true;
    for(int i=1;i<=n;i++) {
        if( !dp[a[i]] ) {
            for(int j=a[i];j<=lim;j++)
                dp[j] |= dp[j-a[i]];
            m++;
        }
    }
    printf("%d
", m);
}
int main() {
    int T;
    scanf("%d", &T);
    for(int i=1;i<=T;i++)
        solve();
    return 0;
}