https://codeforces.com/problemset/problem/997/A


题目大意:
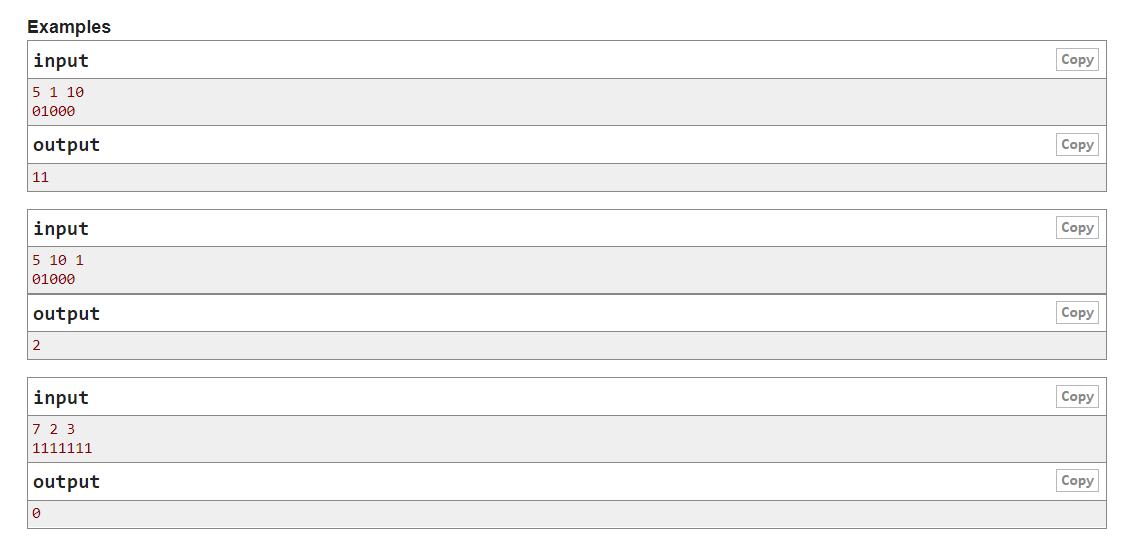
给定一串0-1序列,定义两种操作:
操作一:选取一连续串倒置。
操作二:选取一连续串把进行01互换(取反)。
并给出操作一和操作二的代价,分别为x和y。
操作到最后要把串变成只含1的串,问最小的操作代价。
假定连续0的段数是num,那么可以知道,每进行一次操作一,就可以减少一次操作二的次数。
因此就要考虑操作一和二的优先使用问题:
如果x<y 就优先倒置,把所有0块区间合成一个0块区间,然后取反,代价(num-1)*x+y
如果x>y 直接把每个0块区间取反好了,代价 num*y
1 #include <stdio.h> 2 #include <string.h> 3 #include <iostream> 4 #include <string> 5 #include <math.h> 6 #include <algorithm> 7 #include <vector> 8 #include <stack> 9 #include <queue> 10 #include <set> 11 #include <map> 12 #include <math.h> 13 const int INF=0x3f3f3f3f; 14 typedef long long LL; 15 const int mod=1e9+7; 16 #define Bug cout<<"---------------------"<<endl 17 const int maxn=3e5+10; 18 using namespace std; 19 20 char str[maxn]; 21 22 int main() 23 { 24 int n,x,y; 25 scanf("%d %d %d",&n,&x,&y); 26 int op = x<=y? 0:1; 27 scanf("%s",str); 28 int pre = 1;//上一个字符 29 int num = 0;//连续0段数 30 for(int i = 0;i < n;i++) 31 { 32 if(str[i] == '0' && pre == 1) 33 num++; 34 pre = str[i]-'0'; 35 } 36 LL ans = 0; 37 if(op==0&&num!=0)//优先操作一 38 ans=(LL)(num-1)*x+y;//注意结果要类型转换为long long 39 else 40 ans=(LL)num*y;//注意结果要类型转换为long long 41 printf("%lld ",ans); 42 return 0; 43 }