https://www.luogu.com.cn/problem/P1024
Description
有形如:ax3+bx2+cx+d=0 这样的一个一元三次方程。
给出该方程中各项的系数(a,b,c,d 均为实数),并约定该方程存在三个不同实根(根的范围在-100至100之间),且根与根之差的绝对值>=1。要求三个实根。
Input
四个实数:a,b,c,d
Output
由小到大依次在同一行输出这三个实根(根与根之间留有空格),并精确到小数点后2位
Sample Input
1 -5 -4 20
Sample Output
-2.00 2.00 5.00
HINT
数据规模和约定
|a|,|b|,|c|,|d|<=10
记方程f(x)=0,若存在2个数x1和x2,且x1<x2,f(x1)×f(x2)<0,则在(x1,x2)之间一定有一个根。
这题解法比较多
因为区间很大,所以可以二分。
题目保证三个答案都在[-100,100]范围内,且两个根的差的绝对值>=1,所以每一个大小为1的区间里至多有1个解。
当区间的两个端点的函数值异号时区间内一定有一个解,这个时候我们可以在区间内进行二分查找ans,如果同号则该区间一定没有解。
刚开始遍历i从-10000到10000了,然后i再除以100当成x的值,没想到这样显示TLE了。。。
1 #include <stdio.h> 2 #include <iostream> 3 #include <string> 4 #include <string.h> 5 #include <algorithm> 6 #include <map> 7 #include <vector> 8 #include <set> 9 #include <stack> 10 #include <queue> 11 #include <math.h> 12 #include <sstream> 13 using namespace std; 14 typedef long long LL; 15 const int INF=0x3f3f3f3f; 16 const int maxn=1e5+10; 17 const double eps = 1e-8; 18 const double PI = acos(-1); 19 20 double a,b,c,d;//开成double吧,免得出错 21 vector<double> ans; 22 double f(double x) 23 { 24 return a*x*x*x+b*x*x+c*x+d; 25 } 26 27 double solve(double x1,double x2) //在x1和x2中二分找答案 28 { 29 double L=x1,R=x2; 30 while(R-L>1e-4) //这里的eps一般要比题中要求的精度(1e-2)多两位。 31 { 32 double mid=(L+R)/2; 33 double t1=f(L); 34 double t2=f(mid); 35 double t3=f(R); 36 if(t2==0) return mid; 37 if(t1*t2<0) R=mid; 38 else if(t2*t3<0) L=mid; 39 } 40 return (L+R)/2;//返回L,R,(L+R)/2都行 41 } 42 43 int main() 44 { 45 #ifdef DEBUG 46 freopen("sample.txt","r",stdin); 47 #endif 48 49 scanf("%lf %lf %lf %lf",&a,&b,&c,&d); 50 double pre=f(-100.0); 51 for(int i=-100;i<=100;i++) 52 { 53 double t=f(i); 54 if(t!=0) 55 { 56 if(t*pre<0) ans.push_back(solve(i-1,i)); 57 } 58 else ans.push_back(i); 59 pre=t; 60 } 61 for(int i=0;i<3;i++) 62 printf(i==2?"%.2f ":"%.2f ",ans[i]); 63 64 return 0; 65 }
下面是我看别的大佬写的
盛金公式:
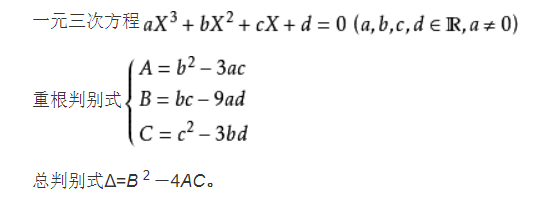


1 #include <iostream> 2 #include <math.h> 3 #include <iomanip> 4 using namespace std; 5 int main() 6 { 7 double a,b,c,d; 8 double as,bs,t,si; 9 double x1,x2,x3; 10 cin>>a>>b>>c>>d; 11 as=b*b-3*a*c; 12 bs=b*c-9*a*d; 13 t=(2*as*b-3*a*bs)/(2*sqrt(as*as*as)); 14 si=acos(t); 15 x1=(-b-2*sqrt(as)*cos(si/3))/(3*a); 16 x2=(-b+sqrt(as)*(cos(si/3)+sqrt(3)*sin(si/3)))/(3*a); 17 x3=(-b+sqrt(as)*(cos(si/3)-sqrt(3)*sin(si/3)))/(3*a); 18 cout<<fixed<<setprecision(2)<<x1<<" "; 19 cout<<fixed<<setprecision(2)<<x3<<" "; 20 cout<<fixed<<setprecision(2)<<x2<<" "; 21 return 0; 22 }
最后是EarthGiao大佬写的题解:
导数+勘根定理+牛顿迭代.
先对函数求导,f'(x)=3ax^2+2*bx+c.
然后直接求根公式求f'(x)=0的点,也就是函数极点.
这题保证有三个不定根,所以有两个单峰.
我们分别设这两个点为p,q.
然后显然的必有三个根在[-100,p),[p,q],(q,100]三个区间内 (两极点间必定存在零点,勘根定理).
然后用神奇的牛顿迭代法多次迭代就好了.
1 #include<iostream> 2 #include<cstdio> 3 #include<cmath> 4 #define eps 1e-4 5 using namespace std; 6 double x1,x2,x3,a,b,c,d; 7 double f(double x){return a*x*x*x+b*x*x+c*x+d;} 8 double df(double x){return 3*a*x*x+2*b*x+c;} 9 double slove(double l,double r) 10 { 11 double x,x0=(l+r)/2; 12 while(abs(x0-x)>eps) 13 x=x0-f(x0)/df(x0),swap(x0,x); 14 return x; 15 } 16 int main() 17 { 18 cin>>a>>b>>c>>d; 19 double p=(-b-sqrt(b*b-3*a*c))/(3*a); 20 double q=(-b+sqrt(b*b-3*a*c))/(3*a); 21 x1=slove(-100,p),x2=slove(p,q),x3=slove(q,100); 22 printf("%.2lf %.2lf %.2lf",x1,x2,x3); 23 return 0; 24 }
-