假设:
H0:You are not pregnant
H1:You are pregnant


Type I and type II errors - wiki
type I error is the rejection of a true nullhypothesis (also known as a "false positive" finding), (假阳性)
type II error is failing to reject a false null hypothesis (also known as a "false negative" finding). (假阴性)
我们要构建零假设,这就是我们要攻击的目标,我们需要使用我们的数据来拒绝它。
常见的做法是我们需要构建统计量,在H0的假设下,统计量往往有一个分布,当我们计算出统计量处于分布的小概率区域中时,我们就可以说零假设是小概率事件,可以拒绝零假设。
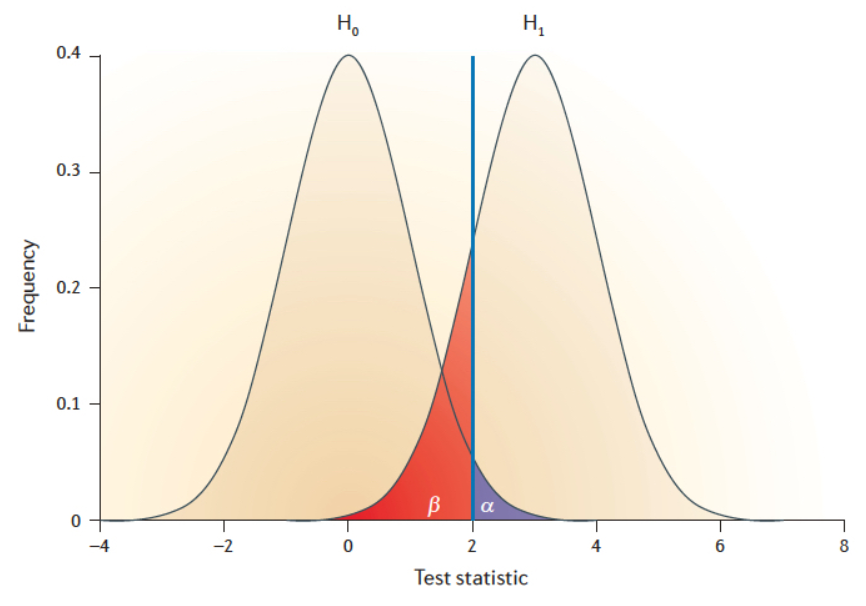
如下图的单侧假设检验,当统计量大于2时,我们就可以拒绝H0,此时我们犯第一类错误地概率就是α,就是零假设是真的,我们却拒绝了它。
当设定了显著性水平后,α就定了,一般为0.05,所以统计量水平也就定了,下图为2. 第二类错误就是,即使没有达到拒绝H0的标准(统计量小于2),但是其实H1是真的,我们却拒绝了它。定义为β。也可以叫做我们接受了错误地H0。
结论:
第一类错误:错误地拒绝了H0
第二类错误:错误地拒绝了H1,换句话说,错误地接受了H0,接受了假的H0,真的很绕口,但是确实一个东西。
与wiki定义完美吻合!!!
参考:
https://www.cnblogs.com/leezx/p/9226078.html
https://www.zhihu.com/question/20993864