topcoder srm 525 div1

problem1 link

最后剩下的是中间的一个矩形．所以可以直接枚举这个矩形，如果它含有的硬币个数等于$K$，则再计算移动的最少次数，更新答案．

problem2 link

首先，每个节点发送每种消息最多只发送一次；其次，在得到消息之后一定是马上发送而不是等待一会儿再发送；最后一点是，如果第$i$天发送了一种消息，一定可以在第$i+1$天发送另外一种消息．

现在的问题是，一个节点同时有两种消息时，应该首先发送哪一种．这个可以$2^{n}$枚举第一次发送的消息类型，然后模拟即可．在模拟过程中可能会出现先来的消息不是枚举的第一次发送的类型．这个可以直接结束这种情况，因为一定会枚举到一种情况，其他节点都一样，而这个节点是先发送另一种状态．

problem3 link

首先，如果将给出的矩阵看作是$n$个顶点的有向图，那么交换$i,j$行列得到的新图相当于两个顶点交换标号，即顶点$i$变为$j$，顶点$j$变为$i$．

那么题目就是要对给出的图重新标号，使得与目标图匹配．

对于$n=8$来说，如果画出目标图，是下面的样子：

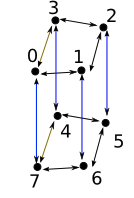
设$p_{i}$表示目标图的第$i$个顶点是原图的第$p_{i}$个顶点．那么对于$n=8$来说，确定了$p_{0},p_{1},p_{n-1}$后，与$p_{1}$相连且不与$p_{n-1}$相连的就是$p_{2}$，同时与$p_{1}$和$p_{n-1}$相连的是$p_{6}$．

也就是说由$p_{1},p_{7}$可找到$p_{2},p_{6}$．同理，由$p_{2},p_{6}$可找到$p_{3},p_{5}$，最后就是$p_{4}$.查找的过程如下图所示（第一幅图找到$p_{2},p_{6}$，第二幅图找到$p_{3},p_{5}$）

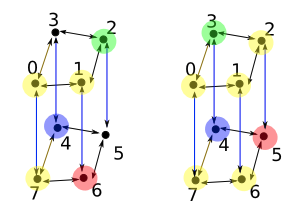
最后一个问题就是如果有了这个数组$p$，求最少的交换次数．$p$中的数组组成了若干个环，对于每个环$C$，需要的交换次数为$|C|-1$

code for problem1

#include <vector>
#include <string>
#include <algorithm>
using namespace std;

class DropCoins {
  public:
    int getMinimum(vector <string> board, int K) {
      const int n = (int)board.size();
      const int m = (int)board[0].size();
      int result = -1;
      vector<vector<int>> f(n + 1, vector<int>(m + 1, 0));
      for (int i = 1; i <= n; ++ i) {
        for (int j = 1; j <= m; ++ j) {
          f[i][j] = f[i - 1][j] + f[i][j - 1] - f[i - 1][j - 1];
          if (board[i - 1][j - 1] == 'o') {
            ++ f[i][j];
          }
        }
      }
      for (int left = 1; left <= m; ++ left) {
        for (int right = left; right <= m; ++ right) {
          for (int up = 1; up <= n; ++ up) {
            for (int down = up; down <= n; ++ down) {
              int cnt = f[down][right] - f[down][left - 1] - f[up - 1][right]
                + f[up - 1][left - 1];
              if (cnt == K) {
                int cost = Cost(left - 1, m - right) + Cost(up - 1, n - down);
                if (result == -1 || result > cost) {
                  result = cost;
                }
              }
            }
          }
        }
      }
      return result;
    }

  private:
    int Cost(int x, int y) {
      return std::min(x + x + y, x + y + y);
    }
};

code for problem2

#include <iostream>
#include <string>
#include <vector>
using namespace std;

class Rumor {
  public:
  int getMinimum(string knowledge, vector<string> graph)
  {
    const int n = (int)graph.size();
    int result = -1;
    for (int mask = 0; mask < (1 << n); ++ mask) {
      int cost = calculate(mask, knowledge, graph);
      if (cost != -1 && (result == -1 || result > cost)) {
        result = cost;
      }
    }
    return result;
  }

  private:

  int getFirstType(int mask, int i) {
    return (mask & (1 << i)) ? 2 : 1;
  }
  int getSecondType(int mask, int i) {
    return (mask & (1 << i)) ? 1 : 2;
  }
  int calculate(const int mask, const string& knowledge, 
      const vector<string>& graph) {
    const int n = (int)knowledge.size();
    long long preGetMessageState = 0;
    long long currentKnowMessageState = 0;
    int preBroadcastMask = 0;
    int day = 0;
    for (int i = 0; i < n; ++ i) {
      if (knowledge[i] == 'Y') {
        preGetMessageState |= 3ll << (i << 1);
      }
    }
    int sendedMessageMask = 0;
    currentKnowMessageState = preGetMessageState;
    const long long finalState = (1ll << (n + n)) - 1;
    while (currentKnowMessageState != finalState) {
      ++ day;
      int nowBroadcastState = 0;
      long long nowGetMessageState = 0;
      for (int i = 0; i < n; ++ i) {
        int type = -1;
        if (preBroadcastMask & (1 << i)) {
          type = getSecondType(mask, i);
        }
        else if (!(sendedMessageMask & (1 << i))) {
          int t = (preGetMessageState >> (i + i)) & 3;
          if (t != 0) {
            if (t & getFirstType(mask, i)) {
              type = getFirstType(mask, i);
            }
            else {
              return -1;
            }
          }
        }
        if (type == -1) {
          continue;
        }
        for (int j = 0; j < n; ++ j) {
          if (graph[i][j] == 'Y') {
            nowGetMessageState |= ((long long)type) << (j + j);
          }
        }
        if (type == getSecondType(mask, i)) {
          sendedMessageMask |= 1 << i;
        }
        else {
          nowBroadcastState |= 1 << i;
        }
      }
      long long currentAll = currentKnowMessageState | nowGetMessageState;
      if (currentAll == currentKnowMessageState) {
        return -1;
      }
      currentKnowMessageState = currentAll;
      preGetMessageState = nowGetMessageState;
      preBroadcastMask = nowBroadcastState;
    }
    return day;
  }
};

code for problem３

#include <vector>
#include <string>
#include <algorithm>
using namespace std;


class MonochromePuzzle {
  public: 
    int getMinimum(vector <string> board) {
      const int n = (int)board.size();
      for (int i = 0; i < n; ++ i) {
        int cnt = 0;
        for (int j = 0; j < n; ++ j) {
          if (board[i][j] == '#') {
            ++ cnt;
          }
        }
        if (cnt != 3) {
          return -1;
        }
      }
      int result = -1;
      for (int i = 0; i < n; ++ i) {
        for (int j = 0; j < n; ++ j) {
          if (i == j) {
            continue;
          }
          for (int k = 0; k < n; ++ k) {
            if (k == i || k == j) {
              continue;
            }
            if (board[i][j] != '#' || board[i][k] != '#') {
              continue;
            }
            int tmp = calculate(i, j, k, board);
            if (tmp != -1 && (result == -1 || result > tmp)) {
              result = tmp;
            }
          }
        }
      }
      return result;
    }
  private:
    int calculate(const int p0, const int p1, const int p2,
        const vector<string>& board) {
      const int n = (int)board.size();
      vector<int> p(n, 0);
      vector<int> used(n, 0);
      p[0] = p0;
      p[1] = p1;
      p[n - 1] = p2;
      used[p0] = used[p1] = used[p2] = 1;
      int x = 1, y = n - 1;
      int a = 2, b = n - 2;
      while (a < b) {
        int ta = -1, tb = -1;
        for (int i = 0; i < n; ++ i) {
          if (used[i] == 0 && board[p[x]][i] == '#') {
            if (board[p[y]][i] == '#') {
              tb = i;
            }
            else {
              ta = i;
            }
          }
        }
        if (ta == -1 || tb == -1) {
          return -1;
        }
        p[a] = ta;
        p[b] = tb;
        used[ta] = used[tb] = 1;
        x = a ++;
        y = b --;
      }
      for (int i = 0; i < n; ++ i) {
        if (used[i] == 0 && board[p[x]][i] == '#' && 
            board[p[y]][i] == '#' && board[p[n - 1]][i] == '#') {
           p[a] = i;
           return getCost(p);
        }
      }
      return -1;
    }
    int getCost(const vector<int>& p) {
      const int n = (int)p.size();
      vector<int> visited(n, 0);
      int result = n;
      for (int i = 0; i < n; ++ i) {
        if (visited[i]) {
          continue;
        }
        int current = i;
        while (visited[current] == 0) {
          visited[current] = 1;
          current = p[current];
        }
        result -= 1;
      }
      return result;
    }
};