problem1 link
设第一个数字为$x$,那么第2到第$n$个数字都可以表示成$a+bx$的形式,其中$b=1$或者$b=-1$.然后可以求出关于$x$的一些范围,求交集即可.
problem2 link
设$f[i][r][g][b]$表示前$i$个已经染色完毕,第$i$颜色为$(r,g,b)$的概率.假设由$(r,g,b)$可以转移到的状态个数为$T$,那么每个可以转移到的状态$(r^{'},g^{'},b^{'})$都可以得到$frac{f[i][r][g][b]}{T}$的贡献.暴力转移的复杂度太高.如果没有$d_{1}$的限制,那么$r,g,b$可以转移到的状态,如果将其看作三维空间中的坐标,是以$(r,g,b)$为中心的边长为$2d_{2}+1$的立方体.这样的更新可以整块进行.有了$d_{1}$,可以将至少有一个大于等于$d_{1}$改为所有的情况减去都小于$d_{1}$的情况.这样的话,$r,g,b$可以转移到的状态为以$r,g,b$为中心的边长为$2d_{2}+1$的立方体去掉以$r,g,b$为中心的边长为$2d_{1}+1$的立方体.
problem3 link
首先,由于10=2*5.这样将问题分解为计算模2以及模5的种类数.然后乘起来即可.考虑计算这个子问题.令$p=2$或者$5$.
由于如果$output[i]=0$,那么对应的区间一定有至少一个0,反之,一定是一个0也不会有.那么可以将$N$个数字分成两部分,一定不会出现0的部分以及可能有0的部分.
(1)对于可能有0的部分的计算:设$f[i][j]$表示放置了前$i$个数字,最后一个放置0的位置在$j$的方案数.
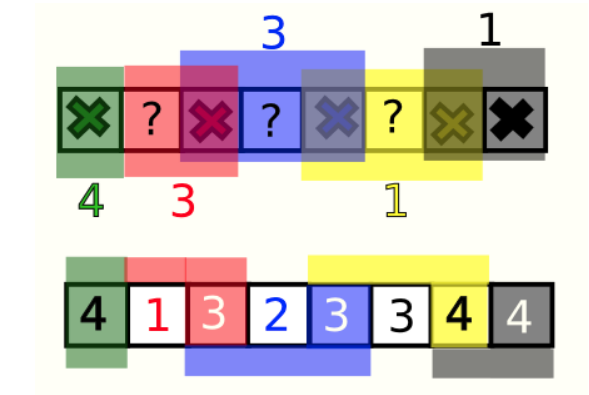
(2)对于一定没有0的部分的计算:首先,如果两个不同的区间$[L_{1},R_{1}],[L_{2},R_{2}]$的关系是$L_{1}=L_{2}$或者$R_{1}=R_{2}$,那么可以将其中一个较大的区间强行分成两段.这样最后所有的区间的两两之间的关系一定以下三种:不相交,一个是另一个的真子集,相交但是不是真子集.如下图所示,有绿,红,蓝,黄,黑5个区间.对于每个区间来说,如果区间内前面的元素确定了,那么区间的最后一个元素就是唯一的(因为$p$是素数).这样的话,只有问号的位置是可以随意放置的.
code for problem1
#include <vector>
#include <string>
#include <limits>
using namespace std;
class ImportantSequence {
public:
int getCount(vector<int> B, string operators) {
int64_t left = 1;
int64_t right = std::numeric_limits<int64_t>::max();
int64_t a = 0;
int b = 1;
for (size_t i = 0; i < B.size(); ++i) {
int64_t val = static_cast<int64_t>(B[i]);
if (operators[i] == '+') {
a = val -a;
b = -b;
} else {
a = a - val;
}
if (b == 1) {
left = std::max(left, 1 - a);
} else {
right = std::min(right, a - 1);
}
if (left > right) {
return 0;
}
}
if (right == std::numeric_limits<int64_t>::max()) {
return -1;
}
return static_cast<int>(right - left + 1);
}
};
code for problem2
#include <algorithm>
#include <cstring>
#include <iostream>
const int MAXN = 40;
const int MAX = 50;
double f[MAXN][MAX + 1][MAX + 1][MAX + 1];
class RandomColoring {
public:
double getProbability(int N, int maxR, int maxG, int maxB, int startR,
int startG, int startB, int d1, int d2) {
this->max_r = maxR;
this->max_g = maxG;
this->max_b = maxB;
f[0][startR][startG][startB] = 1;
for (int i = 1; i < N; ++i) {
for (int r = 0; r < maxR; ++r) {
const std::pair<int, int> rd2 = ComputeRage(r, d2, maxR);
const std::pair<int, int> rd1 = ComputeRage(r, d1 - 1, maxR);
for (int g = 0; g < maxG; ++g) {
const std::pair<int, int> gd2 = ComputeRage(g, d2, maxG);
const std::pair<int, int> gd1 = ComputeRage(g, d1 - 1, maxG);
for (int b = 0; b < maxB; ++b) {
const std::pair<int, int> bd2 = ComputeRage(b, d2, maxB);
const std::pair<int, int> bd1 = ComputeRage(b, d1 - 1, maxB);
const int s1 = Size(rd2) * Size(gd2) * Size(bd2);
const int s0 = d1 > 0 ? Size(rd1) * Size(gd1) * Size(bd1) : 0;
if (s1 == s0) {
continue;
}
const double e = f[i - 1][r][g][b] / (s1 - s0);
Add(i, rd2.first, gd2.first, bd2.first, rd2.second, gd2.second,
bd2.second, e);
if (d1 > 0) {
Add(i, rd1.first, gd1.first, bd1.first, rd1.second, gd1.second,
bd1.second, -e);
}
}
}
}
for (int r = 0; r < maxR; ++r) {
for (int g = 0; g < maxG; ++g) {
for (int b = 0; b < maxB; ++b) {
f[i][r][g][b] += Get(i, r - 1, g, b) + Get(i, r, g - 1, b) +
Get(i, r, g, b - 1) - Get(i, r - 1, g - 1, b) -
Get(i, r - 1, g, b - 1) - Get(i, r, g - 1, b - 1) +
Get(i, r - 1, g - 1, b - 1);
}
}
}
}
double result = 0;
for (int x = 0; x < maxR; ++x) {
for (int y = 0; y < maxG; ++y) {
for (int z = 0; z < maxB; ++z) {
if (!(abs(x - startR) <= d2 && abs(y - startG) <= d2 &&
abs(z - startB) <= d2 &&
(abs(x - startR) >= d1 || abs(y - startG) >= d1 ||
abs(z - startB) >= d1))) {
result += f[N - 1][x][y][z];
}
}
}
}
return result;
}
double Get(int t, int x, int y, int z) {
if (x >= 0 && y >= 0 && z >= 0) {
return f[t][x][y][z];
}
return 0.0;
}
void Add(int t, int x, int y, int z, int x1, int y1, int z1, double val) {
Add(t, x, y, z, val);
Add(t, x, y, z1 + 1, -val);
Add(t, x, y1 + 1, z, -val);
Add(t, x1 + 1, y, z, -val);
Add(t, x1 + 1, y1 + 1, z, val);
Add(t, x1 + 1, y, z1 + 1, val);
Add(t, x, y1 + 1, z1 + 1, val);
Add(t, x1 + 1, y1 + 1, z1 + 1, -val);
}
void Add(int t, int x, int y, int z, double val) {
if (x < max_r && y < max_g && z < max_b) {
f[t][x][y][z] += val;
}
}
std::pair<int, int> ComputeRage(int x, int d, int max_x) {
return {std::max(0, x - d), std::min(x + d, max_x - 1)};
}
int Size(const std::pair<int, int> &range) {
return range.second - range.first + 1;
}
private:
int max_r, max_g, max_b;
};
code for problem3
#include <string>
#include <vector>
#include <limits>
#include <iostream>
using namespace std;
class ProductQuery {
static const int64_t mod = 1000000007;
public:
int theInput(int N, vector<int> Qfrom, vector<int> Qto, vector<int> output) {
auto ModFunc = [output](const int p) -> std::vector<int> {
std::vector<int> r;
for (auto x : output) {
r.push_back(x % p);
}
return r;
};
return static_cast<int>(Compute(N, Qfrom, Qto, ModFunc(2), 2) *
Compute(N, Qfrom, Qto, ModFunc(5), 5) %
mod);
}
private:
int64_t Compute(int N, const std::vector<int> &qfrom,
const std::vector<int> &qto, const std::vector<int> &output,
const int p) {
std::vector<int> not_zero(N, 0);
for (size_t i = 0; i < output.size(); ++i) {
if (0 != output[i]) {
for (int j = qfrom[i]; j <= qto[i]; ++j) {
not_zero[j] = 1;
}
}
}
int zero_index = 0;
int not_zero_index = 0;
std::vector<int> zero_map(N, -1);
std::vector<int> not_zero_map(N, -1);
for (int i = 0; i < N; ++i) {
if (not_zero[i] == 0) {
zero_map[i] = zero_index++;
} else {
not_zero_map[i] = not_zero_index++;
}
}
std::vector<int> zero_qfrom;
std::vector<int> zero_qto;
std::vector<int> not_zero_qfrom;
std::vector<int> not_zero_qto;
std::vector<int> not_zero_output;
auto FindValidRange = [](const std::vector<int> &elements, int left,
int right) -> std::pair<int, int> {
int left_index = -1;
int right_index = -1;
for (int j = left; j <= right; ++j) {
if (elements[j] != -1) {
if (left_index == -1) {
left_index = elements[j];
}
right_index = elements[j];
}
}
return {left_index, right_index};
};
for (size_t i = 0; i < output.size(); ++i) {
if (output[i] == 0) {
auto r = FindValidRange(zero_map, qfrom[i], qto[i]);
if (r.first == -1) {
return 0;
}
zero_qfrom.push_back(r.first);
zero_qto.push_back(r.second);
} else {
auto r = FindValidRange(not_zero_map, qfrom[i], qto[i]);
if (r.first == -1) {
return 0;
}
not_zero_qfrom.push_back(r.first);
not_zero_qto.push_back(r.second);
not_zero_output.push_back(output[i]);
}
}
return Place0(zero_index, zero_qfrom, zero_qto, p) *
NotPlace0(not_zero_index, not_zero_qfrom, not_zero_qto,
not_zero_output, p) %
mod;
}
int64_t Place0(int N, const std::vector<int> &qfrom,
const std::vector<int> &qto, const int p) {
if (N == 0) {
return 1;
}
auto CheckForceZero = [qfrom, qto](int pre_zero_index,
int cur_index) -> bool {
for (size_t i = 0; i < qfrom.size(); ++i) {
if (qfrom[i] > pre_zero_index && qto[i] == cur_index) {
return true;
}
}
return false;
};
auto EncodeIndex = [](int t) { return t + 1; };
std::vector<std::vector<int64_t>> f(N, std::vector<int64_t>(N + 1, 0));
f[0][EncodeIndex(0)] = 1;
if (!CheckForceZero(-1, 0)) {
f[0][EncodeIndex(-1)] = p - 1;
}
for (int i = 1; i < N; ++i) {
for (int j = -1; j < i; ++j) {
const int64_t val = f[i - 1][EncodeIndex(j)];
Add(f[i][EncodeIndex(i)], val);
if (!CheckForceZero(j, i)) {
Add(f[i][EncodeIndex(j)], val * (p - 1) % mod);
}
}
}
int64_t result = 0;
for (int i = -1; i < N; ++i) {
Add(result, f[N - 1][EncodeIndex(i)]);
}
return result;
}
int64_t NotPlace0(int N, const std::vector<int> &qfrom,
const std::vector<int> &qto, const std::vector<int> &output,
const int p) {
if (N == 0) {
return 1;
}
std::vector<int64_t> rev_table(p);
for (int i = 1; i < p; ++i) {
for (int j = 1; j < p; ++j) {
if (i * j % p == 1) {
rev_table[i] = j;
break;
}
}
}
std::vector<bool> delete_items(output.size(), false);
std::vector<int> last_qfrom = qfrom;
std::vector<int> last_qto = qto;
std::vector<int> last_output = output;
bool updated = true;
int total_range = static_cast<int>(output.size());
while (updated) {
updated = false;
for (size_t i = 0; i < output.size(); ++i) {
if (!delete_items[i]) {
for (int j = i + 1; j < output.size(); ++j) {
if (!delete_items[j]) {
if (last_qfrom[i] == last_qfrom[j] && last_qto[i] == last_qto[j]) {
if (last_output[i] != last_output[j]) {
return 0;
}
--total_range;
delete_items[j] = true;
updated = true;
} else if (last_qfrom[i] == last_qfrom[j]) {
if (last_qto[i] < last_qto[j]) {
last_qfrom[j] = last_qto[i] + 1;
last_output[j] =
last_output[j] * rev_table[last_output[i]] % p;
} else {
last_qfrom[i] = last_qto[j] + 1;
last_output[i] =
last_output[i] * rev_table[last_output[j]] % p;
}
updated = true;
} else if (last_qto[i] == last_qto[j]) {
if (last_qfrom[i] < last_qfrom[j]) {
last_qto[i] = last_qfrom[j] - 1;
last_output[i] =
last_output[i] * rev_table[last_output[j]] % p;
} else {
last_qto[j] = last_qfrom[i] - 1;
last_output[j] =
last_output[j] * rev_table[last_output[i]] % p;
}
updated = true;
}
}
}
}
}
}
int64_t result = 1;
for (int i = 1; i <= N - total_range; ++i) {
result = result * (p - 1) % mod;
}
return result;
}
void Add(int64_t &x, int64_t y) {
x += y;
if (x >= mod) {
x -= mod;
}
}
};