problem1 link
因为数据比较小,直接开一个二维数组记录哪些格子已经遍历,哪些还没有。进行模拟即可。
problem2 link
模拟一些小数据,可以发现,AB的形状以及要求的区间是下面的样子:
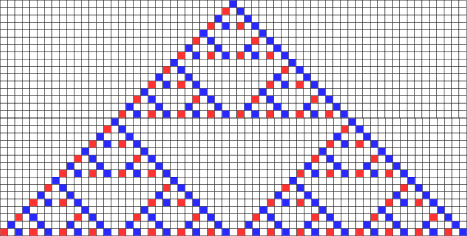
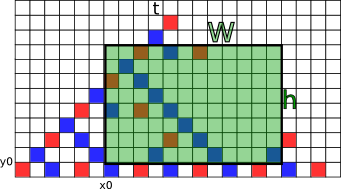
对于每个答案中的格子,直接去找它是哪种格子即可。每一次$x$都会变为原来的三分之一。
problem3 link
首先,可以求出需要的最少改变的次数。在最少的改变次数之后的改变一定是对每个改变的位置改变了至少三次(3的倍数),这样的话代价一定是$costs[0]+costs[1]+costs[2]$的倍数。所以可以求出最多的改变次数,设为$K$。
设$d_{1}$表示当前多少个位置需要$3t+1$步才能完成,$d_{2}$表示当前多少个位置需要$3t+2$步才能完成.那么需要$3t$步的位置为$n-d_{1}-d_{2}$.$n$为串的长度。每次修改的转移是:
(1)修改了$d_{2}$中的一个,那么转移为$(d_{1},d_{2})$到($d_{1}+1,d_{2}-1)$
(2)修改了$d_{1}$中的一个,那么转移为$(d_{1},d_{2})$到($d_{1}-1,d_{2})$
(1)修改了$n-d_{1}-d_{2}$中的一个,那么转移为$(d_{1},d_{2})$到($d_{1},d_{2}+1)$
现在二元组$(d_{1},d_{2})$可以表示一个状态,所有的状态最多有$p=frac{(n+1)(n+2)}{2}$。将状态编号。所有转移可以用一个矩阵表示。现在可以得到一个转移的矩阵$A$,那么答案就是$A^{0}+A^{1}+...+A^{K}$,这个可以用二分计算,复杂度为$log(K)*p^{3}$.
这里有一个优化是增加一个状态表示“成功”,设其编号为$p+1$,设状态$(0,0)$的编号为$q$,那么$A[q][p+1]=1,A[p+1][p+1]=1$。这样计算$A^{K+1}$即可。
code for problem1
#include <stdio.h>
#include <iostream>
#include <vector>
using namespace std;
class RotatingBot {
public:
int minArea(vector<int> moves) {
int min_x = 0;
int max_x = 0;
int min_y = 0;
int max_y = 0;
int dx[] = {0, -1, 0, 1};
int dy[] = {1, 0, -1, 0};
int current_x = 0;
int current_y = 0;
int current_direction = 0;
std::vector<Segment> pre_segments;
auto Go = [&](int step) {
int next_x = current_x + dx[current_direction] * step;
int next_y = current_y + dy[current_direction] * step;
Segment current_segment{current_x, current_y, next_x, next_y};
pre_segments.push_back(current_segment);
min_x = std::min(min_x, next_x);
max_x = std::max(max_x, next_x);
min_y = std::min(min_y, next_y);
max_y = std::max(max_y, next_y);
current_direction = (current_direction + 1) & 3;
current_x = next_x;
current_y = next_y;
};
for (size_t i = 0; i < moves.size() && i < 4; ++i) {
Go(moves[i]);
}
if (moves.size() <= 3) {
return (max_x - min_x + 1) * (max_y - min_y + 1);
}
if (pre_segments[3].y2 > 0) {
return -1;
} else if (pre_segments[3].y2 == 0) {
if (pre_segments[3].y2 == 0 &&
(pre_segments[3].x2 >= 0 ||
((moves.size() > 4) && (pre_segments[3].x2 < -1)))) {
return -1;
}
} else {
if (moves.size() > 4 && pre_segments[3].x2 < 0) {
return -1;
}
}
const int N = max_x - min_x + 1;
const int M = max_y - min_y + 1;
std::vector<std::vector<bool>> grid(N, std::vector<bool>(M, false));
auto Fill = [&](const Segment &s) {
if (s.x1 == s.x2) {
for (int i = std::min(s.y1, s.y2); i <= std::max(s.y1, s.y2); ++i) {
grid[s.x1][i] = true;
}
} else {
for (int i = std::min(s.x1, s.x2); i <= std::max(s.x1, s.x2); ++i) {
grid[i][s.y1] = true;
}
}
};
auto FindEnd = [&](int x, int y, int direction) -> std::pair<int, int> {
do {
int new_x = x + dx[direction];
int new_y = y + dy[direction];
if (new_x < 0 || new_x >= N || new_y < 0 || new_y >= M ||
grid[new_x][new_y]) {
return {x, y};
}
x = new_x;
y = new_y;
} while (true);
};
for (Segment &s : pre_segments) {
s.Move(-min_x, -min_y);
Fill(s);
}
current_x -= min_x;
current_y -= min_y;
max_x -= min_x;
max_y -= min_y;
min_x = min_y = 0;
for (size_t i = 4; i < moves.size(); ++i) {
auto end = FindEnd(current_x, current_y, current_direction);
int direction = current_direction;
Go(moves[i]);
Segment s = pre_segments.back();
if (direction == 0) {
if (s.y2 > end.second ||
((i + 1 < moves.size()) && (s.y2 < end.second))) {
return -1;
}
} else if (direction == 1) {
if (s.x2 < end.first ||
((i + 1 < moves.size()) && (s.x2 > end.first))) {
return -1;
}
} else if (direction == 2) {
if (s.y2 < end.second ||
((i + 1 < moves.size()) && (s.y2 > end.second))) {
return -1;
}
} else {
if (s.x2 > end.first ||
((i + 1 < moves.size()) && (s.x2 < end.first))) {
return -1;
}
}
Fill(s);
}
return (max_x - min_x + 1) * (max_y - min_y + 1);
}
private:
struct Segment {
int x1;
int y1;
int x2;
int y2;
void Move(int diff_x, int diff_y) {
x1 += diff_x;
x2 += diff_x;
y1 += diff_y;
y2 += diff_y;
}
};
};
code for problem2
#include <iostream>
#include <string>
#include <vector>
using namespace std;
class CheckerExpansion {
public:
vector<string> resultAfter(long long t, long long x0, long long y0, int w,
int h) {
std::vector<std::string> result(h);
for (int i = 0; i < h; ++i) {
std::string s = "";
for (int j = 0; j < w; ++j) {
s += Compute(t, x0 + j + 1, y0 + h - i - 1 + 1);
}
result[i] = s;
}
return result;
}
private:
char Compute(long long t, long long x, long long y) {
if (x + y > t + t) {
return '.';
}
long long current_width = 1L;
long long current_height = 1L;
while (current_width < x || current_height < y) {
current_width = (current_width << 1) + 1;
current_height <<= 1;
}
auto IsInside = [](long long x, long long y, long long width,
long long height) {
return 1 <= x && x <= width && 1 <= y && y <= height &&
x + y <= height + height && x >= y;
};
while (current_width > 3) {
long long width = current_width >> 1;
long long height = current_height >> 1;
if (IsInside(x, y, width, height)) {
} else if (IsInside(x - width - 1, y, width, height)) {
x -= width + 1;
} else if (IsInside(x - height, y - height, width, height)) {
x -= height;
y -= height;
} else {
return '.';
}
current_width = width;
current_height = height;
}
if (x == 1 && y == 1) {
return 'A';
}
if ((x == 2 && y == 2) || (x == 3 && y == 1)) {
return 'B';
}
return '.';
}
};
code for problem3
#include <iostream>
#include <map>
#include <string>
#include <vector>
using namespace std;
class ConversionMachine {
static constexpr int mod = 1000000007;
using Matrix = std::vector<std::vector<int>>;
public:
int countAll(string word1, string word2, vector<int> costs, int maxCost) {
auto ComputeCost = [&](char from, char to) -> long long {
int id1 = static_cast<int>(from - 'a');
int id2 = static_cast<int>(to - 'a');
long long result = 0;
while (id1 != id2) {
result += static_cast<long long>(costs[id1]);
id1 = (id1 + 1) % 3;
}
return result;
};
auto ComputeDist = [&](char from, char to) -> int {
int id1 = static_cast<int>(from - 'a');
int id2 = static_cast<int>(to - 'a');
return (id2 - id1 + 3) % 3;
};
const int N = static_cast<int>(word1.size());
long long total_moves = 0;
int type1 = 0;
int type2 = 0;
for (int i = 0; i < N; ++i) {
long long r = ComputeCost(word1[i], word2[i]);
if (static_cast<long long>(maxCost) < r) {
return 0;
}
int t = ComputeDist(word1[i], word2[i]);
total_moves += t;
if (t == 1) {
++type1;
} else if (t == 2) {
++type2;
}
maxCost -= static_cast<int>(r);
}
long long total = static_cast<long long>(costs[0]) +
static_cast<long long>(costs[1]) +
static_cast<long long>(costs[2]);
total_moves += static_cast<long long>(maxCost) / total * 3;
std::map<std::pair<int, int>, int> index_map;
int index = 0;
for (int d1 = 0; d1 <= N; ++d1) {
for (int d2 = 0; d1 + d2 <= N; ++d2) {
index_map[std::make_pair(d1, d2)] = index++;
}
}
index++;
Matrix transform_table(index, std::vector<int>(index, 0));
for (auto &from : index_map) {
int d1 = from.first.first;
int d2 = from.first.second;
int id = from.second;
if (d2 > 0) {
transform_table[id][index_map[std::make_pair(d1 + 1, d2 - 1)]] = d2;
}
if (d1 > 0) {
transform_table[id][index_map[std::make_pair(d1 - 1, d2)]] = d1;
}
if (N - d1 - d2 > 0) {
transform_table[id][index_map[std::make_pair(d1, d2 + 1)]] =
N - d1 - d2;
}
}
transform_table[index_map[{0, 0}]][index - 1] = 1;
transform_table[index - 1][index - 1] = 1;
Matrix result_table = Pow(transform_table, total_moves + 1);
int from_idx = index_map[std::make_pair(type1, type2)];
return result_table[from_idx][index - 1];
}
private:
Matrix UnitMatrix(size_t n) {
Matrix r(n, std::vector<int>(n, 0));
for (size_t i = 0; i < n; ++i) {
r[i][i] = 1;
}
return r;
}
Matrix Pow(Matrix t, long long p) {
Matrix r = UnitMatrix(t.size());
while (p > 0) {
if ((p & 1) == 1) {
r = Multiply(r, t);
}
t = Multiply(t, t);
p >>= 1;
}
return r;
}
Matrix Multiply(const Matrix &left, const Matrix &right) {
Matrix r(left.size(), std::vector<int>(left.size(), 0));
for (size_t i = 0; i < left.size(); ++i) {
for (size_t j = 0; j < left.size(); ++j) {
for (size_t k = 0; k < left.size(); ++k) {
int t = static_cast<int>(static_cast<long long>(left[i][k]) *
static_cast<long long>(right[k][j]) % mod);
Add(r[i][j], t);
}
}
}
return r;
}
void Add(int &x, int y) {
x += y;
if (x >= mod) {
x -= mod;
}
}
};