首先声明,我是一个菜鸟。一下文章中出现技术误导情况盖不负责
我们首先分析度温场的求解吧,假设边界条件和初始条件经已设定。在贴码代之前,我们先谈谈这个类要需什么属性和行为:节点组数用于存储盘算变量、网格小大、度维定义、盘算函数,也就这么多了。如何盘算某节点的度温?盘算其东南西北方位相接节点对该节点的穿导热之和便可,读者这里可以虑考一下如何添加源相和对流换热进去。
package Soong.Solver
{
public class TSolver
{
public var Tlist:Vector.<Node>;
private var xGridNum:uint = 1;//Number of Grid Allocated in X Direction
private var yGridNum:uint = 1;//Number of Grid Allocated in X Direction
public var dx:Number = 1;//Grid Size in X Direction
public var dy:Number = 1;//Grid Size in Y Direction
public var Sx:Number = 0;//Area of Heat Interface in X Direction
public var Sy:Number = 0;//Area of Heat Interface in X Direction
public var cellVol:Number = 0;//Volume of Control Volume
public var Freezing:Boolean=false;//If Time to Freeze
public function TSolver(xGridNum:uint,yGridNum:uint,dx:Number,dy:Number)
{
this.xGridNum = xGridNum;
this.yGridNum = yGridNum;
this.dx = dx;
this.dy = dy;
this.Sx = dy * 1;
this.Sy = dx * 1;
this.cellVol = dx * dy * 1;
}
public function Step(timeStep:Number):void
{
var col:uint = 0;
var row:uint = 0;
var node:Node = null;
for (col = 2; col < xGridNum - 2; col++ )
{
for (row = 2; row < yGridNum-2; row++ )
{
node = Tlist[Index(col, row)] as Node;
CalTnext(timeStep,node,col,row);
node.T0=node.T;
}
}
}
public function CalTnext(timeStep:Number,node:Node,col:uint,row:uint):void
{
var conner:Boolean=false;
var node_Adj:Node = null;
var conductionHeat:Number = 0;
//For Node on/in Connor or Edge
var SxFix:Number=1;//Area Fix Factor For Non-Interior Region in X Direction
var SyFix:Number=1;//Area Fix Factor For Non-Interior Region in Y Direction
var VolFix:Number=1;//Volume Fix Factor For Non-Interior Region in Y Direction
if(((col==2)&&(row==2))||((col==2)&&(row==yGridNum-3))||((col==xGridNum-3)&&(row==2))||((col==xGridNum-3)&&(row==yGridNum-3)))
{
SxFix=1/2.0;
SyFix=1/2.0;
conner=true;
}
if((col==2)||(col==xGridNum-3))
{
VolFix/=2;
if(!conner)
{
SyFix=1/2.0;
}
}
if((row==2)||(row==yGridNum-3))
{
VolFix/=2;
if(!conner)
{
SxFix=1/2.0;
}
}
node_Adj = Tlist[Index(col+1, row)] as Node;
conductionHeat+=node.eHeatExchangeFactor*(node_Adj.T0-node.T0)*Sx*SxFix;
node_Adj = Tlist[Index(col-1, row)] as Node;
conductionHeat+=node.wHeatExchangeFactor*(node_Adj.T0-node.T0)*Sx*SxFix;
node_Adj = Tlist[Index(col, row+1)] as Node;
conductionHeat+=node.nHeatExchangeFactor*(node_Adj.T0-node.T0)*Sy*SyFix;
node_Adj = Tlist[Index(col, row - 1)] as Node;
conductionHeat+=node.sHeatExchangeFactor*(node_Adj.T0-node.T0)*Sy*SyFix;
var dT:Number = conductionHeat * timeStep;
dT /= cellVol * VolFix * node.Rho * node.Cp;
node.T = node.T0 + dT;
}
public function LatentHeatRelease(node:Node):void
{
}
//Apply the Boundary Condition
public function ApplyBC():void
{
}
private function Index(col:uint=0,row:uint=0):uint
{
return row * xGridNum + col;
}
}
}
简略吧,要需意注的是不同置位的节点其传热面积以及控制体体积不尽相同,要需Fix一下。这里给出开端的盘算结果(代迭100s的结果)。前目笔者没有贴出全部码代,这时按照笔者供提的序程是法无运行的,读者想一想,还点缺什么?
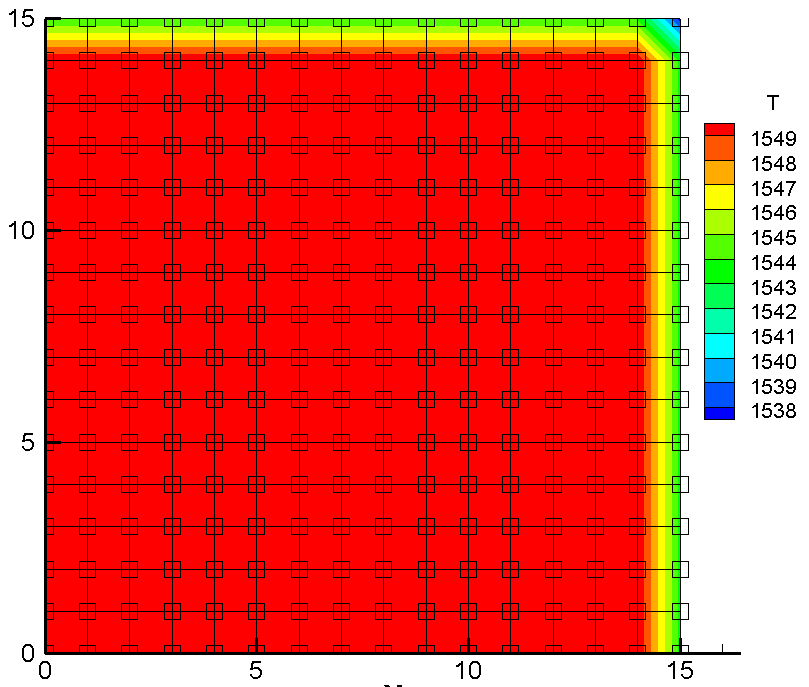
将其称对到得整个界面:
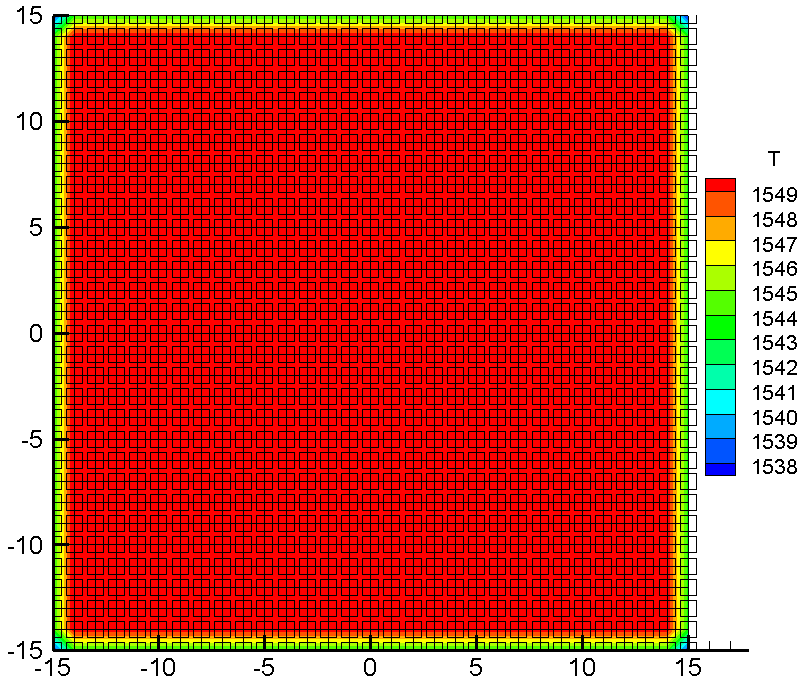
有点子样了,这还不是终究的盘算结果,凝结潜热还没有虑考进去,后续会补上。另外,我们没有离散偏微分方程,但是我们的方法和离散偏微分方程归同途殊的。或许读者可以解理无限差分和无限容积的连续与区别了。
文章结束给大家分享下程序员的一些笑话语录:
一个合格的程序员是不会写出 诸如 “摧毁地球” 这样的程序的,他们会写一个函数叫 “摧毁行星”而把地球当一个参数传进去。