数据结构与算法 -- 图

一、图的表示方式

997：找到小镇的法官

题目描述：在一个小镇里，按从 1 到 N 标记了 N 个人。传言称，这些人中有一个是小镇上的秘密法官。

如果小镇的法官真的存在，那么：

1. 小镇的法官不相信任何人。
2. 每个人（除了小镇法官外）都信任小镇的法官。
3. 只有一个人同时满足属性 1 和属性 2 。

给定数组 trust，该数组由信任对 trust[i] = [a, b] 组成，表示标记为 a 的人信任标记为 b 的人。如果小镇存在秘密法官并且可以确定他的身份，请返回该法官的标记。否则，返回 -1。

示例 1：输入：N = 2, trust = [[1,2]]，输出：2

示例 2：输入：N = 3, trust = [[1,3],[2,3]]，输出：3

示例 3：输入：N = 3, trust = [[1,3],[2,3],[3,1]]，输出：-1

示例 4：输入：N = 3, trust = [[1,2],[2,3]]，输出：-1

示例 5：输入：N = 4, trust = [[1,3],[1,4],[2,3],[2,4],[4,3]]，输出：3

 提示：

1. 1 <= N <= 1000
2. trust.length <= 10000
3. trust[i] 是完全不同的
4. trust[i][0] != trust[i][1]
5. 1 <= trust[i][0], trust[i][1] <= N

解题思路：这道题就是要找到一个人，他被所有人相信，但是不相信所有人。我们可以联系到图，相信与被相信分别对应到图的出度和入度，每个人代表一个点。我们要找的就是在这N个点里面有没有一个点符合：出度为0，入度为N-1。

代码实现（java）:

class Solution {
    public int findJudge(int N, int[][] trust) {
        int in_degree[]=new int [N+1];//入度，即相信我的人数
        int out_degree[]=new int [N+1];//出度，即我相信的人数
        //遍历信任数组
        int len = trust.length;
        for(int i=0;i<len;i++){
　　　　　　  //相信别人的人的出度+1
            out_degree[trust[i][0]]++;
            //被人相信的人的入度+1
            in_degree[trust[i][1]]++;
        }
        for(int i=1;i<=N;i++){
　　　　　　　//符合要求的条件：出度为0，入度为N-1
            if((out_degree[i]==0) & (in_degree[i]==N-1)){
                return i;
            }
        }
        return -1;
    }
}

1042、不邻接植花

题目描述：有N个花园，按从1到N标记。在每个花园中，你打算种下四种花之一。paths[i]=[x,y]描述了花园x到花园y的双向路径。另外，没有花园有3条以上的路径可以进入或者离开。你需要为每个花园选择一种花，使得通过路径相连的任何两个花园中的花的种类互不相同。

以数组形式返回选择的方案作为答案 answer，其中 answer[i] 为在第 (i+1) 个花园中种植的花的种类。花的种类用 1, 2, 3, 4 表示。保证存在答案。

示例 1：输入：N = 3, paths = [[1,2],[2,3],[3,1]]，输出：[1,2,3]
示例 2：输入：N = 4, paths = [[1,2],[3,4]]，输出：[1,2,1,2]
示例 3：输入：N = 4, paths = [[1,2],[2,3],[3,4],[4,1],[1,3],[2,4]]，输出：[1,2,3,4]

提示：
1 <= N <= 10000
0 <= paths.size <= 20000
不存在花园有 4 条或者更多路径可以进入或离开。
保证存在答案。

解题思路：遍历邻接数组，找出每个节点的邻节点，构造出图，然后用邻节点没有用过的一个颜色将当前节点染色即可。

class Solution {

    public int[] gardenNoAdj(int N, int[][] paths) {
        //1、构造图：创建描述节点与邻节点关系图
        Map<Integer, Set<Integer>> graph = new HashMap<>();
        for(int i=0; i<N; i++) {
            graph.put(i, new HashSet<Integer>());
        }
        for(int[] path : paths) {
            //互相邻接
            graph.get(path[0]-1).add(path[1]-1);
            graph.get(path[1]-1).add(path[0]-1);
        }
        
        //着色结果数组
        int[] answer = new int[N];
        //2、遍历着色
        for(int i=0; i<N; i++) {
            //必须知道当前节点的邻节点都着了哪些颜色，因此需要一个颜色数组，标记当前颜色是否已经使用过了
            boolean[] colorUsed = new boolean[5];//由于颜色是从1开始，所以此处使用5而不是4，因为第0个元素仅占位而没有任何作用
            for(int nextNode : graph.get(i)) {
                colorUsed[answer[nextNode]] = true;
            }
            //当前节点的邻节点使用的颜色确定了，遍历已使用的颜色数组，即可确定当前节点的颜色
            for(int j=1; j<colorUsed.length; j++) {
                //如果当前颜色没有使用，则当前节点使用该颜色
                if(!colorUsed[j]) {
                    answer[i] = j;
                    break;
                }
            }
        }
        
        return answer;
    }
}

 二、广度优先搜索算法（BFS）

994、腐烂的橘子

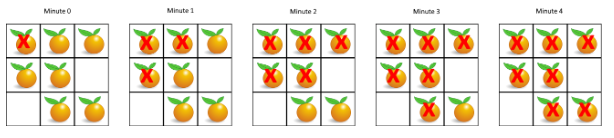
题目描述：每分钟，任何与腐烂的橘子（在 4 个正方向上）相邻的新鲜橘子都会腐烂。返回直到单元格中没有新鲜橘子为止所必须经过的最小分钟数。如果不可能，返回 -1。

示例 1：输入：[[2,1,1],[1,1,0],[0,1,1]]，输出：4

示例 2：输入：[[2,1,1],[0,1,1],[1,0,1]]，输出：-1；解释：左下角的橘子（第 2 行， 第 0 列）永远不会腐烂，因为腐烂只会发生在 4 个正向上。

示例 3：输入：[[0,2]]，输出：0；解释：因为 0 分钟时已经没有新鲜橘子了，所以答案就是 0 。

提示：

1 <= grid.length <= 10
1 <= grid[0].length <= 10
grid[i][j] 仅为 0、1 或 2

解题思路：腐烂的橘子会把靠近他的新鲜的橘子腐蚀，那么就是只要使用BFS从所有腐烂的橘子的位置一层一层往外遍历就可以了。

public class Solution {
    public int orangesRotting(int[][] grid) {
        int row = grid.length, col = grid[0].length, time = 0;
        //保存腐烂的橘子
        Queue<int[]> queue = new LinkedList<>();
        for(int i=0; i<row; i++) {
            for(int j=0; j<col; j++) {
                if(grid[i][j] == 2) {
                    int[] p = {0, i, j};
                    queue.add(p);
                }
            }
        }
        while(!queue.isEmpty()) {
            int[] p = queue.poll();
            time = time>p[0] ? time : p[0];
            //每一分钟都腐烂旁边的橘子
            if(p[1]+1 < row && grid[p[1]+1][p[2]] == 1) {//向下
                grid[p[1]+1][p[2]] = 2;
                int[] po = {p[0]+1, p[1]+1, p[2]};
                queue.add(po);
            }
            if(p[1]-1 >= 0 && grid[p[1]-1][p[2]] == 1) {//向上
                grid[p[1]-1][p[2]] = 2;
                int[] po = {p[0]+1, p[1]-1, p[2]};
                queue.add(po);
            }
            if(p[2]+1 < col && grid[p[1]][p[2]+1] == 1) {//向右
                grid[p[1]][p[2]+1] = 2;
                int[] po = {p[0]+1, p[1], p[2]+1};
                queue.add(po);
            }
            if(p[2]-1 >= 0 && grid[p[1]][p[2]-1] == 1) {//向左
                grid[p[1]][p[2]-1] = 2;
                int[] po = {p[0]+1, p[1], p[2]-1};
                queue.add(po);
            }
        }
        
        //判断所有橘子是否都已经腐烂
        for(int i=0; i<row; i++) {
            for(int j=0; j<col; j++) {
                if(grid[i][j] == 1) {
                    return -1;
                }
            }
        }
        return time;
    }
    
    public static void main(String[] args) {
        Solution solution = new Solution();
        int[][] grid1 = {{2,1,1},{1,1,0},{0,1,1}};
        System.out.println(solution.orangesRotting(grid1));
        int[][] grid2 = {{2,1,1},{0,1,1},{1,0,1}};
        System.out.println(solution.orangesRotting(grid2));
        int[][] grid3 = {{0,2}};
        System.out.println(solution.orangesRotting(grid3));
    }
}

 三、深度优先搜索算法（DFS）

733、图像渲染

题目描述：有一幅以二维整数数组表示的图画，每一个整数表示该图画的像素值大小，数值在 0 到 65535 之间。给你一个坐标 (sr, sc) 表示图像渲染开始的像素值（行 ，列）和一个新的颜色值 newColor，让你重新上色这幅图像。为了完成上色工作，从初始坐标开始，记录初始坐标的上下左右四个方向上像素值与初始坐标相同的相连像素点，接着再记录这四个方向上符合条件的像素点与他们对应四个方向上像素值与初始坐标相同的相连像素点，……，重复该过程。将所有有记录的像素点的颜色值改为新的颜色值。最后返回经过上色渲染后的图像。

示例 1:输入: image = [[1,1,1],[1,1,0],[1,0,1]]，sr = 1, sc = 1, newColor = 2，输出: [[2,2,2],[2,2,0],[2,0,1]]

解析: 在图像的正中间，(坐标(sr,sc)=(1,1)),在路径上所有符合条件的像素点的颜色都被更改成2。注意，右下角的像素没有更改为2，因为它不是在上下左右四个方向上与初始点相连的像素点。

注意:

1、image 和 image[0] 的长度在范围 [1, 50] 内。
2、给出的初始点将满足 0 <= sr < image.length 和 0 <= sc < image[0].length。
3、image[i][j] 和 newColor 表示的颜色值在范围 [0, 65535]内。

public class Solution {
    public static void main(String[] args) {
        Solution solution = new Solution();
        if(solution.visited == null) {
            System.out.println("null");
        }
//        int[][] image = {{1,1,1}, {1,1,0}, {1,0,1}};
//        int[][] result = solution.floodFill(image, 1, 1, 2);
        int[][] image = {{0,0,0}, {0,0,0}};
        int[][] result = solution.floodFill(image, 0, 0, 2);
        System.out.println("");
    }
    //深度优先搜索
    boolean[][] visited;
    public int[][] floodFill(int[][] image, int sr, int sc, int newColor) {
        int row = image.length, col = image[0].length;
        Queue<int[]> queue = new LinkedList<>();
        if(visited == null) {
            visited = new boolean[row][col];
        }
        visited[sr][sc] = true;
        if(sr+1 < row && !visited[sr+1][sc] && image[sr+1][sc] == image[sr][sc]) {
            int[] nextPos = {sr+1, sc};
            visited[sr+1][sc] = true;
            queue.add(nextPos);
        }
        if(sr-1 >= 0 && !visited[sr-1][sc] && image[sr-1][sc] == image[sr][sc]) {
            int[] nextPos = {sr-1, sc};
            visited[sr-1][sc] = true;
            queue.add(nextPos);
        }
        if(sc+1 < col && !visited[sr][sc+1] && image[sr][sc+1] == image[sr][sc]) {
            int[] nextPos = {sr, sc+1};
            visited[sr][sc+1] = true;
            queue.add(nextPos);
        }
        if(sc-1 >= 0 && !visited[sr][sc-1] && image[sr][sc-1] == image[sr][sc]) {
            int[] nextPos = {sr, sc-1};
            visited[sr][sc-1] = true;
            queue.add(nextPos);
        }
        image[sr][sc] = newColor;
        
        while(!queue.isEmpty()) {
            int[] next = queue.poll();
            floodFill(image, next[0], next[1], newColor);
        }
        return image;
    }
    //广度优先搜索
    public int[][] floodFill_BFS(int[][] image, int sr, int sc, int newColor) {
        int row = image.length, col = image[0].length;
        Queue<int[]> queue = new LinkedList<>();
        int[] src = {sr, sc};
        queue.add(src);
        boolean[][] visited = new boolean[row][col];
        while(!queue.isEmpty()) {
            int[] pos = queue.poll();
            if(pos[0]+1 < row && !visited[pos[0]+1][pos[1]] && image[pos[0]+1][pos[1]] == image[pos[0]][pos[1]]) {
                int[] nextPos = {pos[0]+1, pos[1]};
                queue.add(nextPos);
            }
            if(pos[0]-1 >= 0 && !visited[pos[0]-1][pos[1]] && image[pos[0]-1][pos[1]] == image[pos[0]][pos[1]]) {
                int[] nextPos = {pos[0]-1, pos[1]};
                queue.add(nextPos);
            }
            if(pos[1]+1 < col && !visited[pos[0]][pos[1]+1] && image[pos[0]][pos[1]+1] == image[pos[0]][pos[1]]) {
                int[] nextPos = {pos[0], pos[1]+1};
                queue.add(nextPos);
            }
            if(pos[1]-1 >= 0 && !visited[pos[0]][pos[1]-1] && image[pos[0]][pos[1]-1] == image[pos[0]][pos[1]]) {
                int[] nextPos = {pos[0], pos[1]-1};
                queue.add(nextPos);
            }
            image[pos[0]][pos[1]] = newColor;
            visited[pos[0]][pos[1]] = true;
        }
        return image;
    }
}

200、岛屿数量

题目描述：给定一个由 '1'（陆地）和 '0'（水）组成的的二维网格，计算岛屿的数量。一个岛被水包围，并且它是通过水平方向或垂直方向上相邻的陆地连接而成的。你可以假设网格的四个边均被水包围。

示例 1:

输入:
11110
11010
11000
00000

输出: 1
示例 2:

输入:
11000
11000
00100
00011

输出: 3

解题思路：采用深度优先搜索遍历给定的二维网格，每遇到'1'就把岛屿数量加1，并把访问过的改为‘0’，继续遍历

public class Solution {
    public static void main(String[] args) {
        Solution solution = new Solution();
        char[][] grid1 = {{'1','1','1','1','0'}, {'1','1','0','1','0'}, {'1','1','0','0','0'}, {'0','0','0','0','0'}};
        int result1 = solution.numIslands(grid1);
        System.out.println(result1);
        char[][] grid2 = {{'1','1','0','0','0'}, {'1','1','0','0','0'}, {'0','0','1','0','0'}, {'0','0','0','1','1'}};
        int result2 = solution.numIslands(grid2);
        System.out.println(result2);
    }
    public int numIslands(char[][] grid) {
        if(grid == null || grid.length == 0
                || grid[0].length == 0) {
            return 0;
        }
        int row = grid.length, col = grid[0].length, count = 0;
        /**
         * 每遇到'1'，岛屿数量就加1，并开始向四个方向进行深度优先搜索，
         * 并把搜索过的位置变为'0'，因为相邻的都属于一个island，然后
         * 开始继续找下一个'1'
         */
        for(int i=0; i<row; i++) {
            for(int j=0; j<col; j++) {
                if(grid[i][j] == '1') {
                    count++;
                    dfsSearch(grid, i, j, row, col);
                }
            }
        }
        return count;
    }
    //深度优先搜索
    private void dfsSearch(char[][] grid, int i, int j, int row, int col) {
        //深度搜索终止条件
        if(i<0 || i>=row || j<0 || j>=col || grid[i][j] != '1') {
            return;
        }
        grid[i][j] = '0';
        //方法1：分别向四个方向递归
        dfsSearch(grid, i+1, j, row, col);//向下深度搜索
        dfsSearch(grid, i-1, j, row, col);//向上深度搜索
        dfsSearch(grid, i, j+1, row, col);//向右深度搜索
        dfsSearch(grid, i, j-1, row, col);//向左深度搜索
        //方法2：用一个visited数组，标记遍历过的岛屿
    } 
}