机器学习之马尔科夫随机场

　　马尔科夫随机场是典型的马尔科夫网（MRF），是一个可以由无向图表示的概率分布模型。图中每个结点表示一个或者一组变量，结点之间的边表示两个变量之间的依赖关系。在马尔科夫随机场中存在一组势函数（定义在变量子集上的非负实函数），也称为因子，主要是用于定义概率分布函数。

1、模型的定义

　　首先来了解图的概念，对于图G，结点和边分别记作v和e，结点和边的集合分别记作V和E，则图可以表示为

　　G =（V，E）

　　而对于无向图就是指结点之间的边是没有方向的。

　　概率图模型就是由图表示的概率分布（准确的说就是表示各变量之间的依赖关系）。设有联合概率分布P(Y) 是一组随机变量，给出表示它的无向图G。则这组随机变量位于图中的各结点上。在这里我们引入三个概念：成对马尔科夫性、局部马尔科夫性、全局马尔科夫性，用来表示无向图中随机变量之间的关系。

　　成对马尔科夫性：设u和v是无向图G中任意两个没有边连接的结点（也就是说两个之间没有依赖的关系），结点u和v分别对应随机变量Y_u和Y_v。其他所有结点为O，对应的随机变量组是Y_O。则成对马尔科夫性的表达式如下

　　

　　上面式子的意思是在给定了随机变量组Y_O的条件下随机变量Y_u和Y_v是条件独立的。

　　局部马尔科夫性：设v是无向图G中的任意结点，W是与v有边连接的所有结点，O是v，W以外的所有结点（相当于W将v和O给隔开了）。则在给定W的条件下，v和O之间是相互独立的，表达式如下

　　

　　全局马尔科夫性：设结点集A，B在无向图G中被结点集合C分开的任意结点的集合，具体如下图所示

　　

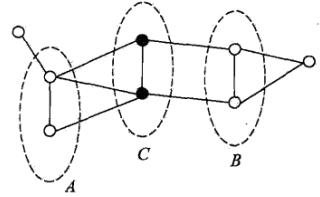
　　则在给定了集合C的条件下结点集合A和B之间是相互独立的，具体表达式如下

　　

　　仔细观察发现这三种性质实质上是等价的，成对马尔科夫性和局部马尔科夫性都可以看作是全局马尔科夫性的特殊形式。那这三种性质提出来有什么用呢？首先满足这三种性质的联合概率分布P(Y)可以称为马尔科夫随机场或者概率无向图模型。而对于马尔科夫随机场，可以将联合概率分布P(Y)拆分成多个因子的乘积，这样就便于计算P(Y)。

2、模型的因子分解

　　首先引入团和最大团的概念。什么是团？在无向图G中，若一个子集中的各个节点两两之间均有边连接，则将该子集称为团。那什么是最大团呢？最大团就是不能被其他团包含的团（对于一个团，当加入一个新的结点之后无法构成团，则称为最大团）。团也等价与势函数。举一个具体的例子来理解

　　

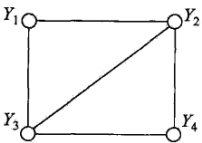
　　对于上图中的无向图模型，团的个数有五个：{Y₁, Y₂}，{Y₂, Y₃}，{Y₃, Y₄}，{Y₄, Y₂}，{Y₁, Y₃}。最大团的个数有两个：{Y₁, Y₂, Y₃}，{Y₂, Y₃, Y₄}。

　　对于我们的联合概率分布P(Y)就可以分解为最大团上的随机变量的函数的乘积，这就是概率无向图模型的因子分解。对于给定的无向图G，C为G上的最大团，Y_C表示C对应的随机变量。那么联合概率分布可以表示为

　　

　　

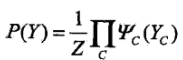
　　在这里函数Ψ_C(Y_C)就是最大团C上的势函数。

　　引入规范场因子Z是为了保证概率P(Y)构成一个概率分布，势函数因为要求是严格正的，因此通常一般定义为指数函数

　　

　　因此对于满足马尔科夫随机场的联合概率分布可以通过因子分解的形式求解。