题目背景
请注意阅读题目中括号里的内容。
(mathbb N):非负整数;(mathbb N*):正整数(没有(0));(mathbb Z):整数。
题目描述
你的面前有(1)条铁轨,这条铁轨在眼前分成(N)条。每条铁轨上都绑着(T_i)个人((T_i in mathbb N* ,0 le i le N))。
每个人都犯了一些罪过,所以他们都应该受到火车的碾压。然而火车只有一个,你只能选择一条道路。
绑在铁轨上的每一个人都有一个“罪过程度”(C_{i,j}(C_{i,j} in mathbb Z),即(C_{i,j})可能是负数)。也就是说,给定一组(i,j),能够唯一确定一个(C_{i,j}),你可以把它看作一个坐标。
同时,你发现,有许多铁轨有岔路,而且还连到了另一条铁轨上。岔路上没有任何绑着的人或分支岔道,没有岔道的两端连接同一条铁轨,而且岔路具有单向性,方向由岔路的左偏或右偏决定(具体见样例)。
现在,你想控制电车,使它碾压过的人的“罪过程度”(sum C)最大。具体操作是:从(N)条铁路中任选一条出发,在不倒车的情况下,开过一些铁轨和岔路,直到电车走到一条铁路的尽头(即这之后没有任何一个绑着的人)为止。
你能解决这个问题吗?
示例:
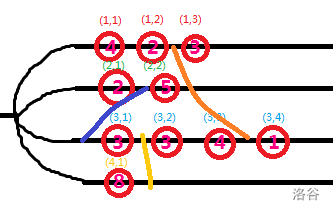
其中红圈表示人,上面有其坐标((i,j)),中间的粉色数字表示(C),还有三条岔路。我们可以用一个点组({(x_1,y_1),(x_2,y_2)})表示岔路的起点和终点。((x_{1or2},y_{1or2}))表示的是端点正前方的人的坐标。特别地,若端点前没有人,则(y_{1or2}=0)。比如说上图的蓝色道路可表示为({(3,0),(2,1)})或({(2,1),(3,0)})。
在图中很明显,若(y_1<y_2),则道路从((x_1,y_1))到达((x_2,y_2))。比如说橙色道路({(1,2),(3,3)}),由于(2<3),所以只能从铁轨(1)走到铁轨(3)而不能反着走。蓝色岔道也同理。
特别地,若(y_1=y_2),则将这条岔道视作双向的。 比如说黄色岔道({(3,1),(4,1)}),既能从(3)号铁轨走向(4)号铁轨,也能反着走。
注意:虽然橙色道路跨越了第(2)条铁轨,但是并不连接。也就是说电车走橙色岔道不能在中途切换到第(2)条铁轨上,走第(2)条铁轨也不能走上橙色岔道。
最好的规划是:先走第(4)条铁轨,碾压了((4,1))后走过黄色岔道,登上第(3)条铁轨,再继续碾压((3,2),(3,3),(3,4)),最后走到第(3)条铁轨的终点,能获得最大(sum C_{max}=16)。
输入格式
第(1)行有两个整数(N,M),分别表示铁轨和岔道的数量。
第(2)行有(N)个整数,第(i)个整数表示(T_i)。
往下(N)行,第(i)行有(T_{i})个整数,其中第(j)个整数表示(C_{i,j})的值。
再往下(M)行,每行会有四个整数(x_1,y_1,x_2,y_2),表示有一条岔路,从坐标为((x_1,y_1))的人的后边连到了((x_2,y_2))的人的后边。
输出格式
仅输出一个整数(Ans),表示你所能碾压的人的“罪过程度”之总和(sum C)的最大值。
输入样例
4 3
3 2 4 1
4 2 3
2 5
3 3 4 1
8
1 2 3 3
3 0 2 1
3 1 4 1
输出样例
16
提示说明
对于所有数据,(N,M,T<1000),对于任意一个(C),(-2^{31}le Cle 2^{31}-1)。
注意时间限制。
题解代码(解释在代码里)
#include <algorithm>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <queue>
/*
* @brief 大体思路:
* @param 1.由于二维坐标直接连边比较困难(当然不排除许多巨佬直接二维连边爆切此题),所以可以转化成一维。
* 以下注释称转化成一维的坐标为“真实数字”。
* @param 2.以含有人最多的铁轨为“Tmax”,将人数不足Tmax的铁轨后面补上一些C=0的人。形成优美的矩形结构(具体见图)。
* @param 3.计算前缀和(基于真实数字),方便之后使用。
* @param 4.通过转化后的点来连边。为了计算两个相邻岔道的端点之间C的总值(即边权),使用前缀和。
* 一条铁轨的第一个岔道端点向起点连边,最后一个岔道端点向终点连边。
* @param 5.使用SPFA跑最长路。
* @brief 时间复杂度(以下的N为总人数(但题目中表示铁轨数,可以理解为题目中的T*N),M为岔道数):
* @param 1.计算前缀和:O(N);
* @param 2.连边(最坏情况,假设每个人的正后方都有铁轨):O(N+M);
* @param 3.跑最长路:O(K(N+M))(数据均随机,K约等于2)。
*/
/////////////////////////
using namespace std;
const int MAXEDGE = 5000001; //最大边数。如果每个人之间都有岔路,那么它的最大值就是sum(T[i]).
const int MAXPOINT = 5000001; //最大点数(即最大人数,显然是sum(T[i]))
const int MAXPATH = 1001; //最大岔道数
const int _ST_TO_FN = 0 /*起点到终点*/, _FN_TO_ST = 1 /*终点到起点*/, _BOTH = 2 /*双向*/; //判定岔道的类别
typedef pair<int, int> point; //点,记录坐标
struct path
{ //岔道
int st /*起点*/, fn /*终点*/;
};
//↓点和真实数字互相转化的工具函数(声明)
int getrange(int, int); //获得前缀和
int getrange(int); //获得一个点到这一行结尾的前缀和
int __realNum(int, int); //!(关键)一个点对应的真实数字
point __Point(int); //将真实数字转换为点
int __dir(path &); //判断岔道的方向
void add_edge(int, int, int); //图加边
int __line_end(int); //返回第n条铁轨的起点对应的真实数字
int __line_head(int); //返回第n条铁轨的终点对应的真实数字
//↑点和真实数字互相转化的工具函数(声明)
//↓链式前向星内容
int head[MAXPOINT], tot;
int ver[MAXEDGE], edge[MAXEDGE], nxt[MAXEDGE];
void add_edge(int st, int fn, int w)
{
ver[++tot] = fn;
edge[tot] = w;
nxt[tot] = head[st];
head[st] = tot;
}
//↑链式前向星内容
//↓题目所有输入的数据保存在这里
int N, M, T[MAXPOINT], C[MAXPOINT]; //N:铁轨数量,M:岔道数量,T[i]:第i条铁轨上绑着的人数,C[i]:真实数字为i的人的罪过程度
bool isthere[MAXPOINT]; //真实数字为i的人的后面是否有一条岔道
path p[MAXPATH]; //所有的岔道
int Tmax = -1; //最大的T
int qzh[MAXPOINT]; //前缀和
//↑题目所有输入的数据保存在这里
//↓点和真实数字互相转化的工具函数(定义)
inline int getrange(int st, int fn)
{
return qzh[fn] - qzh[st];
}
inline int getrange(int st)
{
return qzh[st - (st % Tmax) + Tmax - 1] - qzh[st];
}
inline int __realNum(int x, int y)
{
return (x - 1) * Tmax + y;
}
inline point __Point(int n)
{
return make_pair(n / Tmax + 1, n % Tmax);
}
inline int __dir(path &p)
{
point _st = __Point(p.st), _fn = __Point(p.fn);
if (_st.second < _fn.second)
return _ST_TO_FN;
else if (_st.second > _fn.second)
return _FN_TO_ST;
else
return _BOTH;
}
inline int __line_head(int n)
{
return (n - 1) * Tmax;
}
inline int __line_end(int n)
{
return __line_head(n) + Tmax - 1;
}
//↑点和真实数字互相转化的工具函数(定义)
//↓SPFA
bool vis[MAXPOINT];
int dist[MAXPOINT];
queue<int> q;
int spfa(int start, int finish)
{
memset(dist, 0x3f, sizeof(dist));
memset(vis, 0, sizeof(vis));
dist[start] = 0;
vis[start] = 1;
q.push(start);
while (!q.empty())
{
int x = q.front();
q.pop();
vis[x] = 0;
for (int i = head[x]; i; i = nxt[i])
{
int y = ver[i], z = edge[i];
if (dist[y] > dist[x] + z)
{
dist[y] = dist[x] + z;
if (!vis[y])
q.push(y), vis[y] = 1;
}
}
}
return -dist[finish];
}
//↑SPFA
//设起点编号为-1,终点编号为-2.
int main()
{
ios::sync_with_stdio(false);
cin >> N >> M;
for (int i = 1; i <= N; i++)
{
cin >> T[i];
Tmax = max(Tmax, T[i] + 1);
}
for (int i = 1; i <= N; i++)
{
for (int j = 1; j <= T[i]; j++)
{
int now = __realNum(i, j);
cin >> C[now];
}
}
for (int i = 1; i <= N; i++)
{
for (int j = 0; j < Tmax; j++)
{
int now = __realNum(i, j);
qzh[now] = qzh[now - 1] + C[now];
}
}
for (int i = 1, x1, x2, y1, y2; i <= M; i++)
{
cin >> x1 >> y1 >> x2 >> y2;
p[i].st = __realNum(x1, y1);
p[i].fn = __realNum(x2, y2);
isthere[p[i].st] = isthere[p[i].fn] = true;
if (p[i].st > p[i].fn)
swap(p[i].st, p[i].fn); //不妨设岔道的起点在上方,终点在下方。
switch (__dir(p[i]))
{
case _ST_TO_FN:
add_edge(p[i].st, p[i].fn, 0);
break;
case _FN_TO_ST:
add_edge(p[i].fn, p[i].st, 0);
break;
default: //_BOTH
add_edge(p[i].st, p[i].fn, 0);
add_edge(p[i].fn, p[i].st, 0);
break;
}
}
//处理铁轨
for (int i = 1; i <= N; i++)
{
int pre = __line_head(i);
bool isfirst = true;
for (int now = __line_head(i); now <= __line_end(i); now++)
{
if (isthere[now])
{
//cout<<"find in "<<now<<endl;
if (isfirst)
{ //第一条边,要向起点连
add_edge(-1, now, -getrange(__line_head(i), now));
isfirst = false;
}
else
{
add_edge(pre, now, -getrange(pre, now));
}
pre = now; //前驱转换
}
}
add_edge(pre, -2, -getrange(pre)); //向终点连一条边
}
//spfa跑最长路,完事!
cout << spfa(-1, -2) << endl;//这里估计崩了,忘了负数作为下标访问数组会造成溢出(虽然输出都对)
//system("pause");
return 0;
}