URAL 1137 Bus Routes（欧拉回路路径）

1137. Bus Routes

Time limit: 1.0 second
Memory limit: 64 MB

Several bus routes were in the city of Fishburg. None of the routes shared the same section of road, though common stops and intersections were possible. Fishburg old residents stated that it was possible to move from any stop to any other stop (probably making several transfers). The new mayor of the city decided to reform the city transportation system. He offered that there would be only one route going through all the sections where buses moved in the past. The direction of movement along the sections must be the same and no additional sections should be used.

Write a program, which creates one of the possible new routes or finds out that it is impossible.

Input

The first line of the input contains the number of old routes n. Each of the following n lines contains the description of one route: the number of stops m and the list of that stops. Bus stops are identified by positive integers not exceeding 10000. A route is represented as a sequence of m + 1 bus stop identifiers: l₁, l₂, …, l_m, l_m+1 = l₁ that are sequentially visited by a bus moving along this route. A route may be self-intersected. A route always ends at the same stop where it starts (all the routes are circular).

The number of old routes: 1 ≤ n ≤ 100.
The number of stops: 1 ≤ m ≤ 1000.
The number-identifier of the stop: 1 ≤ l ≤ 10000.

Output

The output contains the number of stops in the new route k and the new route itself in the same format as in the input. The last (k+1)-th stop must be the same as the first. If it is impossible to make a new route according to the problem statement then write 0 (zero) to the output.

Sample

input	output
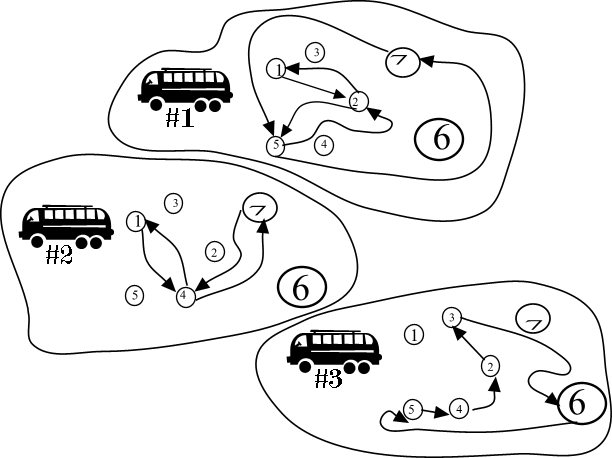
3 6 1 2 5 7 5 2 1 4 1 4 7 4 1 5 2 3 6 5 4 2	15 2 5 4 2 3 6 5 7 4 1 2 1 4 7 5 2

Notes

Here is a picture for the example:

Problem Source: Quarterfinal, Central region of Russia, Rybinsk, October 17-18 2001

【分析】给出一些公交站之间的路（可认为单向），然后让你设计一条回路，包含所有已有的路。

          有向图欧拉回路并输出路径，可用Fleury(弗罗莱)算法。下面是模板。

#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <string>
#include <map>
#include <stack>
#include <queue>
#include <vector>
#define inf 0x3f3f3f3f
#define met(a,b) memset(a,b,sizeof a)
typedef long long ll;
using namespace std;
const int N = 10005;
const int M = 24005;
int n,m,cnt=0;
int tot=0,s,t;
int head[N],dis[N],vis[N][N],pre[N];
int in[N],out[N];
stack<int>st;
struct man {
    int to,next;
} edg[N];
void add(int u,int v) {
    in[v]++;out[u]++;
    edg[tot].to=v;
    edg[tot].next=head[u];
    head[u]=tot++;
}
void dfs(int u){
    for(int i=head[u];i!=-1;i=edg[i].next){
        int v=edg[i].to;
        if(!vis[u][v]){
            vis[u][v]=1;
            dfs(v);
        }
    }
    st.push(u);
}
int main() {
    int u,v,nn=0,sum=0;
    met(head,-1);
    scanf("%d",&n);
    while(n--){
        scanf("%d%d",&m,&u);nn=max(nn,u);sum+=m;
        while(m--){
            scanf("%d",&v);nn=max(nn,v);
            add(u,v);u=v;
        }nn+=m;
    }
    int num=0,start;
    vector<int>vec;
    for(int i=1;i<=nn;i++){
        if(in[i]!=out[i])num++,vec.push_back(in[i]-out[i]);
    }
    if(num!=2||(num==2&&vec[0]!=-1&&vec[1]!=1)||(num==2&&vec[0]!=1&&vec[1]!=-1))puts(0);
    dfs(1);
    printf("%d",sum);
    while(!st.empty()){
        int u=st.top();
        st.pop();
        printf(" %d",u);
    }printf("
");
    return 0;
}