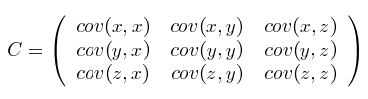理解协方差矩阵

1. 方差和协方差的定义

在统计学中，方差是用来度量单个随机变量的离散程度，而协方差则一般用来刻画两个随机变量的相似程度，其中，方差的计算公式为
 
其中， 表示样本量，符号  表示观测样本的均值。

协方差的计算公式被定义为：

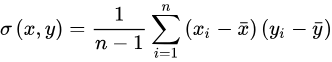
 在公式中，符号  分别表示两个随机变量所对应的观测样本均值，据此，我们发现：方差 可视作随机变量  关于其自身的协方差  .

2. 从方差/协方差到协方差矩阵

根据方差的定义，给定  个随机变量  ，则这些随机变量的方差为

其中，  表示随机变量  中的第  个观测样本，  表示样本量，每个随机变量所对应的观测样本数量均为  。

其中，为方便书写，  表示随机变量  中的第  个观测样本，  表示样本量，每个随机变量所对应的观测样本数量均为  。

因此，协方差矩阵为

其中，对角线上的元素为各个随机变量的方差，非对角线上的元素为两两随机变量之间的协方差，根据协方差的定义，我们可以认定：矩阵  为对称矩阵(symmetric matrix)，其大小为 。

为了便于理解，我们先从两个变量的协方差矩阵来理解：

2.1 两个变量的协方差矩阵

假设我们有 4 个样本，每个样本都有两个变量，也就是两个特征，它们表示如下： ，  ，  ， 

用一个矩阵表示为：

 

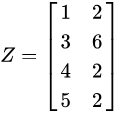
 现在，我们用两个变量空间 ， 来表示这两个特征：

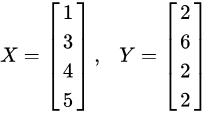
 由于协方差反应的是两个变量之间的相关性，因此，协方差矩阵表示的是所有变量之间两两相关的关系，具体来讲，一个包含两个特征的矩阵，其协方差矩阵应该有 大小：

 

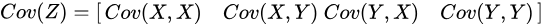
接下来，就来逐一计算  的值。 首先，我们需要先计算出  ，  两个特征空间的平均值：  ，  。 然后，根据协方差的数学定义，计算协方差矩阵的每个元素：

 

 

 

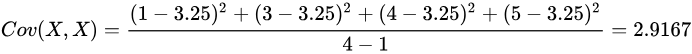
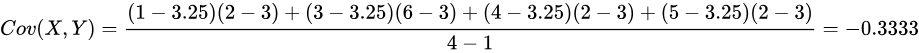
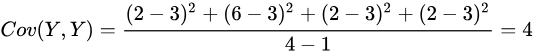
所以协方差矩阵：

我们已经可以从中总结出协方差矩阵  的「计算公式」：

 2.2 多个变量的协方差矩阵

接下来，就用上面推出的计算协方差矩阵的「计算公式」。 假设我们有三个样本：  ，  ，  。 同理我们将它们表示成样本矩阵：

按照上面给出的计算套路，我们需要先计算出矩阵每一列的均值，从左到右分别为：2、3、1.67、3.33。 然后按照上面讲到的公式，计算矩阵每个元素的值，对了，四个变量的协方差矩阵，大小为  ：

....

3. 理解协方差矩阵

这是一个三维的例子，跟上面的例子差不多，只不过换了一种表达方式：