混合高斯模型（Gaussian mixture model, GMM）

1. 前言

这就是为什么我要学习一下二维高斯分布的原因：

总感觉数学知识不够用呐，顺带把混合高斯模型也回顾一下。

2. 单高斯模型(Gaussian single model, GSM）

2.1 一维高斯模型

高斯分布（Gaussian distribution）有时也被称为正态分布（normal distribution），是一种在自然界大量的存在的、最为常见的分布形式。

如果我们对大量的人口进行身高数据的随机采样，并且将采得的身高数据画成柱状图，将会得到如下图1所示的图形。这张图模拟展示了334个成人的统计数据，可以看出图中最多出现的身高在180cm左右2.5cm的区间里。

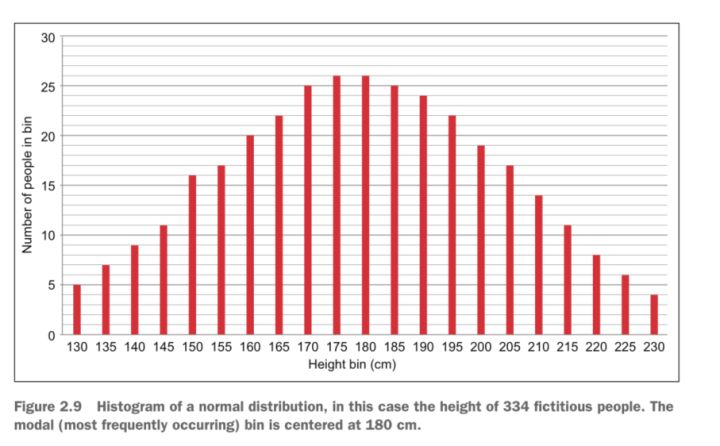
一维高斯分布的概率密度函数如下：

                           

其中  为数据均值（期望），  为数据标准差（Standard deviation）。均值对应正态分布的中间位置，在本例中我们可以推测均值在180cm附近。标准差衡量了数据围绕均值分散的程度。

上面的公式是概率密度函数，也就是在已知参数的情况下，输入变量指x，可以获得相对应的概率密度。还要注意一件事，就是在实际使用前，概率分布要先进行归一化，也就是说曲线下面的面积之和需要为1，这样才能确保返回的概率密度在允许的取值范围内。

如果需要计算指定区间内的分布概率，则可以计算在区间首尾两个取值之间的面积的大小。另外除了直接计算面积，还可以用更简便的方法来获得同样的结果，就是减去区间x对应的累积密度函数（cumulative density function，CDF）。因为CDF表示的是数值小于等于x的分布概率。

3.高斯混合模型(Gaussian mixture model, GMM)

3.1 公式

高斯混合模型是对高斯模型进行简单的扩展，GMM使用多个高斯分布的组合来刻画数据分布。

举例来说：

想象下现在咱们不再考察全部用户的身高，而是要在模型中同时考虑男性和女性的身高。假定之前的样本里男女都有，那么之前所画的高斯分布其实是两个高斯分布的叠加的结果。相比只使用一个高斯来建模，现在我们可以用两个（或多个）高斯分布

                             

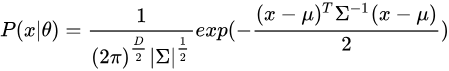
其中，  为数据均值（期望），  为协方差（Covariance），D 为数据维度。

3.2 高斯混合模型

高斯混合模型可以看作是由 K 个单高斯模型组合而成的模型，这 K 个子模型是混合模型的隐变量（Hidden variable）。一般来说，一个混合模型可以使用任何概率分布，这里使用高斯混合模型是因为高斯分布具备很好的数学性质以及良好的计算性能。

举个不是特别稳妥的例子，比如我们现在有一组狗的样本数据，不同种类的狗，体型、颜色、长相各不相同，但都属于狗这个种类，此时单高斯模型可能不能很好的来描述这个分布，因为样本数据分布并不是一个单一的椭圆，所以用混合高斯分布可以更好的描述这个问题，如下图所示

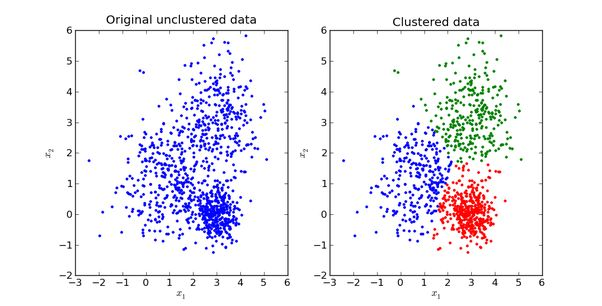
首先定义如下信息：

•  表示第  个观测数据， 
•  是混合模型中子高斯模型的数量， 
•  是观测数据属于第  个子模型的概率，  ， 
•  是第  个子模型的高斯分布密度函数，  。其展开形式与上面介绍的单高斯模型相同
•  表示第  个观测数据属于第  个子模型的概率

高斯混合模型的概率分布为：

对于这个模型而言，参数  ，也就是每个子模型的期望、方差（或协方差）、在混合模型中发生的概率。

 4. 二维高斯分布的参数理解

4.1 均值和协方差矩阵对二维高斯分布的影响

 

 

 

 

 

 

 

 

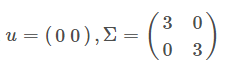
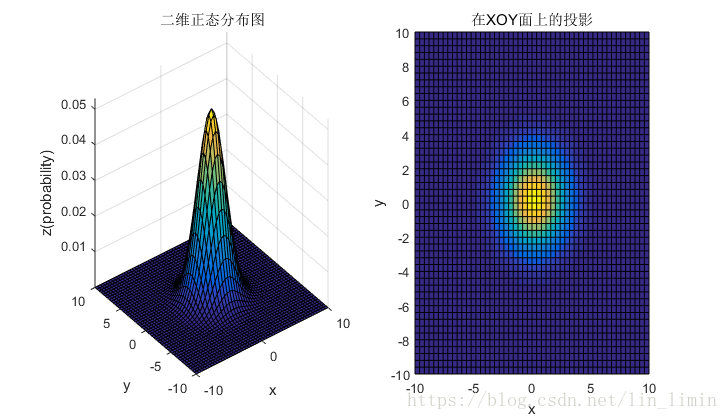
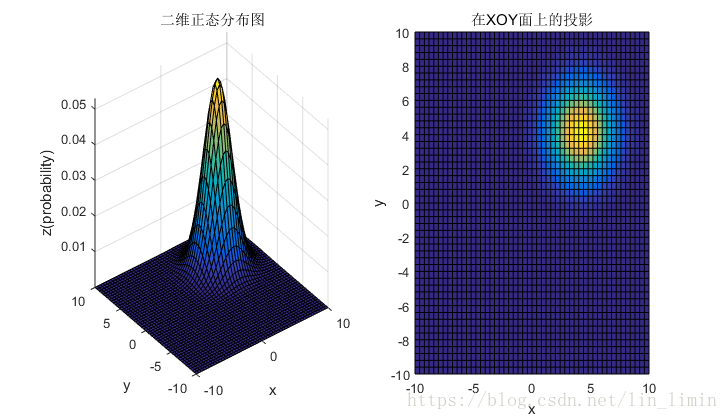
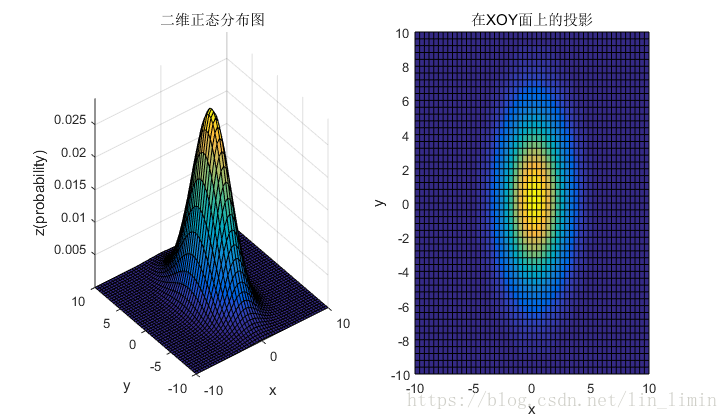
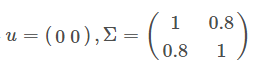
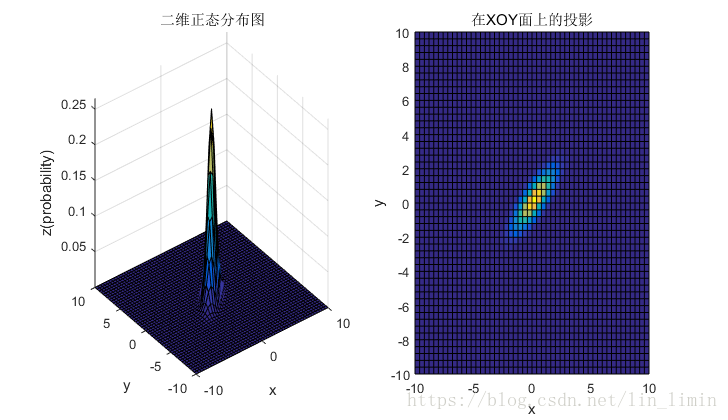
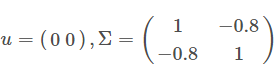
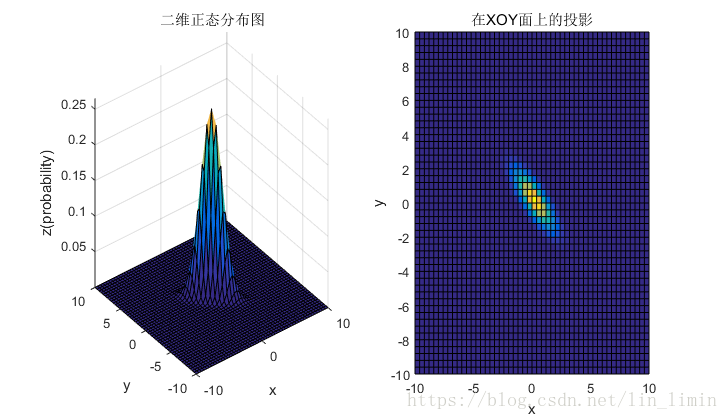
4.2 总结

 

 参考链接：

https://blog.csdn.net/lin_limin/article/details/81024228

https://blog.csdn.net/lin_limin/article/details/81048411

https://zhuanlan.zhihu.com/p/31103654

https://zhuanlan.zhihu.com/p/30483076