PCA原理推导及其在数据降维中的应用

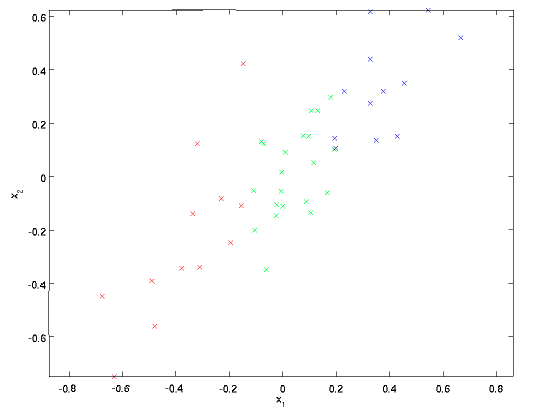
一个信号往往包含多个维度，各个维度之间可能包含较强的相关性。下图表示的是一组二维信号x=(x1,x2)，可以看到数据点基本上分布在x2=x1这条直线上，二者存在很强的相关性（也就是确定x1之后，就能确定x2的大致范围）。

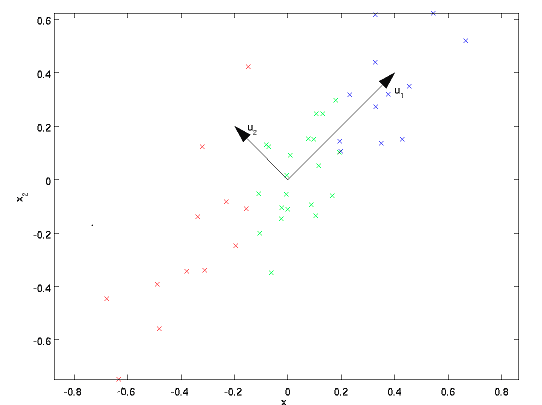
主成分分析（Principal Component Analysis, PCA）的目的在于寻找到一组基，将信号投影到这组基上面，从而能够去除信号各个维度之间的相关性。如下图，u1和u2是通过PCA找到的两个基向量，将信号投影到该基向量上，信号各维度之间的相关性就基本被去除了。

信号各维度之间的相关性可以用相关系数来表示。假设一个维度为x1，另一个维度为x2，二者都相当于随机变量。那么相关系数为：

[ ho=frac{cov(x1,x2)}{sqrt{Var(x1)Var(x2)}} ]

如果两个变量没有相关性，那么相关系数为0。PCA的目的就在于使得信号任意两个维度之间的相关系数都变成0。上式分子为协方差，我们只考虑将协方差变为0。协方差公式如下：

[cov(x_1,x_2)=frac{1}{N}Sigma_{i=1}^N(x_1^{(i)}-ar{x_1})(x_2^{(i)}-ar{x_2}) ]

假设有一组信号，将它们表示为一个矩阵(X_0)，维度为d*N。(X_0)的每一列代表一个信号，d表示信号的维度，N表示有N个信号。X表示各维度去除均值之后的信号。那么信号各维度两两之间的协方差可以表示为一个协方差矩阵：

[S=egin{bmatrix}s_{11}&s_{12}&...&s_{1d}\s_{21}&s_{22}&...&s_{2d}\...\s_{d1}&s_{d2}&...&s_{dd}\end{bmatrix}=frac{1}{N}XX^Tin{R}^{d imes{d}} ]

要去除各维度之间的相关性，相当于让S的非对角元素全变为0，使S对角化。因此我们需要找到一个矩阵U，使S对角化：

[D=U^TSU ]

正好，S的特征向量组成的矩阵能达到这一目的，因此把S的特征向量放入U的每一列中即可。U的列向量即为主成分向量。D为S的特征值组成的对角阵。我们把信号投影到特征向量中，得到的信号为：

[Z=U^TX ]

那么Z的协方差矩阵为：

[S_Z=frac{1}{N}ZZ^T=frac{1}{N}U^TXX^TU=U^TSU=D ]

可见，投影后的信号Z各维度之间不存在相关性。实际中我们不需要将X投影到所有的主成分向量上。可以证明，只需要将X投影到前k个最大特征值对应的特征向量上即可，其余特征向量上的投影分量为噪声。k的数量往往远小于信号原来的维度，因此PCA可以对信号进行降维。只需要通过前k个主成分分量，即可复原原信号，并使恢复误差任意小。

S的维度为d*d。由于实际情况下d很大，远远大于信号个数N，直接求S的特征向量复杂度很高。考虑下面的矩阵：

[S_0=frac{1}{N}X^TXin{R^{N imes{N}}} ]

[S_0u_0=lambda{u_0}Rightarrow{}frac{1}{N}X^TXu_0=lambda{u_0} ]

[Rightarrow{}frac{1}{N}XX^TXu_0=lambda{Xu_0} ]

[Rightarrow{SXu_0=lambda{Xu_0}} ]

可见，可以先求出(S_0)征向量(u_0)，(S)的特征向量为(Xu_0)。由于(S_0)的维度较低，计算量极大地减少。要求(S_0)的特征向量，最直接的方法是做特征值分解。不过由于(S_0)是半正定矩阵，也可以通过SVD来求解。下面证明SVD分解与特征值分解之间的关系。对于一个矩阵A（不一定是方阵），SVD分解如下：

[A=USigma{V^T} ]

[Rightarrow{A}A^T=USigma{V^T}VSigma{U^T}=USigma{^2}U^T ]

[Rightarrow{A}A^TU=USigma{^2} ]

上述第三个等式相当于对(AA^T)做特征值分解，U为(AA^T)的特征值向量矩阵，(Sigma^2)为特征值矩阵。由此可见，要求(AA^T)的特征向量，只需对A做SVD分解，取A的左特征向量矩阵即可。

下面给出MATLAB代码示例。通过PCA分解对ORL人脸库中的人脸图片做降维处理，并用前k个主成分（即最大的k个特征值对应的特征向量）将人脸复原。

PCA代码：

function [avg,U]=fastPCA(X,k)
% X: X的每一列代表一张人脸图片
% k: 降维后的信号维度
%%
avg=mean(X,2);
X=bsxfun(@minus,X,avg);
[~,N]=size(X);
S0=1/N*(X'*X);
[U0,~]=eig(S0);
U0=U0(:,end:-1:1);  % V0原本是按特征值升序排列的，要调换顺序
U=X*U0(:,1:k); % 得到真正协方差矩阵的主成分向量
for i=1:size(U,2)
    U(:,i)=U(:,i)/norm(U(:,i)); % 向量归一化
end

主函数：

% 通过少量几个主成分来恢复人脸
clear;
load orl_data.mat; % 人脸库，每行代表一张人脸图像
k=350; % 把人脸降到k维，用k个主成分恢复人脸
X=Faces; % 矩阵的每一列代表一张人脸
tic;
[avg,U]=fastPCA(X,k);
toc;
X_extract=bsxfun(@minus,X,avg); % 减去均值
X_lowdim=U'*X_extract; % 降维后的图像表达
X_recv=U*X_lowdim;  % 用k个主成分分量恢复人脸
X_recv=bsxfun(@plus,X_recv,avg); % 加上均值
im=reshape(X_recv(:,1),[112,92]);
figure,imshow(im,[]);

% 显示前16个主成分
u=zeros(112,92);
figure
for i=1:16
    u(:)=U(:,i);
    subplot(4,4,i),imshow(u,[]);
end

下图图1为原图，分别用50个主成分、200个主成分和350个主成分复原人脸图像，结果如下：

以下为前16个主成分人脸。可以看到越往后的脸，越不平滑。实际上是因为靠后的脸代表的是人脸的高频分量，包含了更多的细节信息，而靠前的人脸是低频分量，更多地包含了人脸的轮廓。这一点和小波变换是有点像的。