逻辑回归(Logistic Regression,LR)是一种线性分类器,通过logistic函数,将特征映射成一个概率值,来判断输入数据的类别。如下图,纵坐标就是概率。当概率大于0.5,判定为类别1,否则判定为类别0。
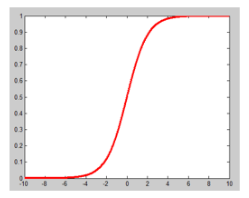
logistic函数的表达式如下,其中w是需要训练的权值:
[ heta(w^Tx)=frac{1}{1+e^{-w^Tx}}
]
逻辑回归的损失函数叫做交叉熵损失函数(cross-entropy loss),下面给出推导过程。
假设数据集符合泊松分布,即
[P(y|x)=egin{cases}p, quad y=1 \ 1-p, quad y=0 end{cases}=p^y(1-p)^{1-y}
]
其中概率p是根据logistic函数计算出来的:
[p=frac{1}{1+e^{-w^Tx}}
]
假设有N个数据点(x_1, x_2, ..., x_N),他们为类别标签分别为(y_1, y_2, ..., y_N)。假设各个数据点之间相互独立,则根据最大似然估计有:
[egin{split} P(Y|X) &=P(y_1,y_2,...,y_N|x_1,x_2,...,x_N) \&=Pi_{i=1}^NP(y_i|x_i) \ &=Pi_{i=1}^Np_i^{y_i}(1-p_i)^{1-y_i} end{split}
]
对等式两边取负对数,得到负对数函数为:
[L(Y|X)=-Sigma_{i=1}^Ny_iln(p_i)+(1-y_i)ln(1-p_i)
]
其中(y_i)代表数据真实的标签,取值为0或1,(p_i)为数据为类别1的概率,取值范围是0到1。负对数函数对N个样本取平均,便得到交叉熵损失函数如下:
[loss(w)=-frac{1}{N}Sigma_{i=1}^Ny_iln(p_i)+(1-y_i)ln(1-p_i)
]
可以看到,当(y_i=1)时,(p_i)越接近1,损失函数越小;当(y_i=0)时,(p_i)越接近0,损失函数越小。因此,通过训练,可以迫使(p_i)趋近于(y_i),从而正确分类。说逻辑回归是线性分类器,这里的线性怎么理解呢?通过Logistic函数可以看到,决定概率值的是(w^Tx)的值。当(w^Tx>0)时,概率值大于0.5,类别为1;当(w^Tx<0)时,概率值小于0.5,类别为0。也就是说,(w^Tx=0)是两类数据的分界面(分类超平面,如下图)。这种用一个超平面将数据进行分类的,就是线性分类器。对应的,如果用一个曲面将数据进行分类,则是非线性分类器了。
