BG:在box-cox变换中,当λ = 0时即为对数变换。
当所分析变量的标准差相对于均值而言比较大时,这种变换特别有用。对数据作对数变换常常起到降低数据波动性和减少不对称性的作用。。这一变换也能有效消除异方差性
library(MASS)
library(openxlsx)
data= read.xlsx("data104.xlsx",sheet = 1) #导入数据
attach(data)
op<-par(mfrow=c(2,2),mar=0.4+c(4,4,1,1),oma=c(0,0,2,0)) #将四张图放在一起,调整边界。(以后也采用此行) plot(size,effort) #图4-4(a) plot(log(size),log(effort)) #图4-4(b) #绘制频率分布直方图 hist(effort) #图4-5(a) hist(size) #图4-5(b)
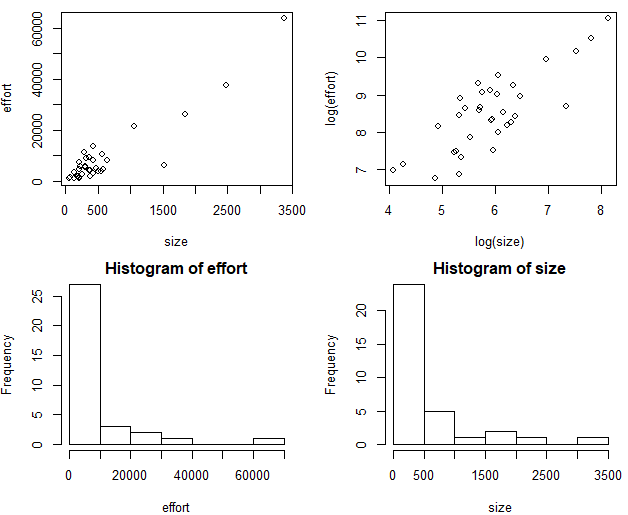
effor 和 size 这两个变量的频率分布图表明,它们并不满足正态分布。为了接近正态分布,必须变换这些变量(通过频率分布图判断变量是否满足正态分布)
1.先进行基本的线性回归,利用得到的模型进行box-cox变换
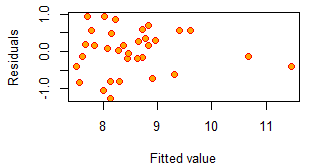
lm1=lm(effort~size+t14) #拟合线性回归模型 summary(lm1) #绘制残差图进行残差分析 plot(fitted(lm1),resid(lm1),cex=1.2,pch=21,col="red",bg="orange",xlab="Fitted value",ylab="Residuals") boxcox(lm1,lambda=seq(0,1,by=0.1)) #进行box-cox变换

从残差图可以看到误差项不满足Gauss-Markov假设。
右图的Box-Cox变换建议问哦们λ可以取在[0.05,0.6]范围内,对投入工作量(effort) 取对数有一定的可信度(λ=0 几乎落在置信域内)
进行对数变换
lm2=lm(log(effort)~size+t14) summary(lm2) #绘制残差图 plot(fitted(lm2),resid(lm2),cex=1.2,pch=21,col="red",bg="orange",xlab="Fitted value",ylab="Residuals")
书上的结果时残差范围大致在[-25,40]内,不满足Gauss-Markov假设
与书上结果不符,上图参擦汗图表示这个模型是可行的。
2.试图拟合 effort 与 log(size),t14 的回归方程。
lm3=lm(effort~log(size)+t14) summary(lm3) #绘制残差图 plot(fitted(lm3),resid(lm3),cex=1.2,pch=21,col="red",bg="orange",xlab="Fitted value",ylab="Residuals") #box-cox变换求λ boxcox(lm3,lambda=seq(0,1,by=0.1))
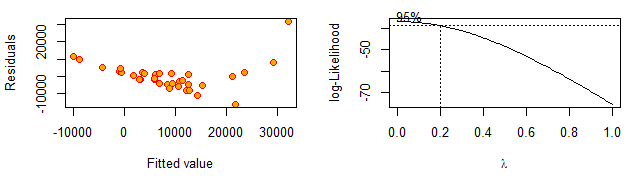
根据右图,Box-Cox变换建议我们取 λ=0
建立如下方程 ln(effort) = β0 + β1ln(size) + β2 t14 + e
lm4=lm(log(effort)~log(size)+t14) #进行线性回归 summary(lm4) #绘制残差图 plot(fitted(lm4),resid(lm4),cex=1.2,pch=21,col="red",bg="orange",xlab="Fitted value",ylab="Residuals") #进行box-cox变换 boxcox(lm4,lambda=seq(0,1,by=0.1))
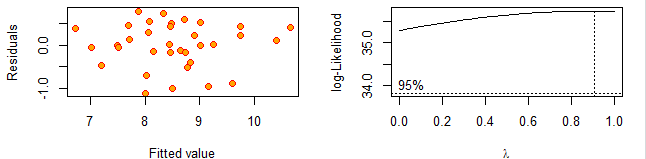
因为λ=1 包含在box-cox图像所示的置信域内,说明不进行变换也是ok的
而且通过残差分析,可以看出这个模型是合理的。