一道好题。想了好久没想出来,只是觉得总要二分独立处理矩形。感觉自己在把问题转化为数学公式以及分解问题的方面的能力很不足。
http://blog.csdn.net/wh2124335/article/details/8739097
解题思路:
考虑每次询问t,对于单一矩形的面积的计算方法~
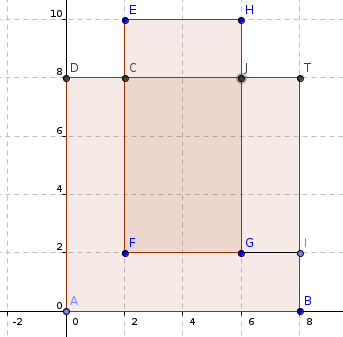
对于询问t。计算如图矩形所被包含的面积可以用矩形面积S[TCFI]-S[TJGI],而S[TCFI]=(t-Fx)*(t-Fy);S[TJGI]=(t-Gx)*(t-Gy)
换句话说就是用[T和矩形左下角的点形成的面积]减去[T和矩形右下角形成的矩形面积]就是这个矩形被包含的面积!
下面来看一个类似的情况:
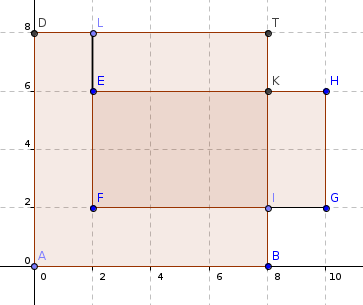
对于这次询问t。当前矩形被包涵的面积是S[TLFI]-S[TLEK]。即[T和矩形左下角点形成的面积]减去[T和矩形左上角点形成的矩形的面积]!
那么对于矩形被包含进(t,t)范围是什么情况呢?
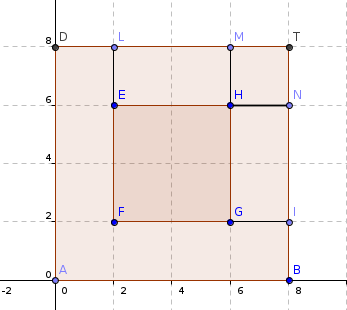
这时候的面积是EHGF的面积,但我们还想计算这个面积时和T有关。仿照前面的讨论,发现S[EHGF]不就是S[TLFI]-S[TLEN]-S[TMGI]+S[TMHN]么?
换句话描述,就是[T和矩形左下角点形成的矩形面积]减去[T和矩形左上角点形成的矩形面积]减去[T和矩形右下角点形成的矩形面积]加上[T和矩形右上角点形成的矩形面积]
那么我们得到了如下算法:
输入询问t
sum=0
遍历所有矩形的四个顶点
如果该顶点在(0,0)-(t,t)的范围内
如果当前顶点是它所在矩形的左上角或右下角的点那么sum+=[(t,t)和该点形成的矩形的面积]
否则sum-=[(t,t)和该点形成的矩形的面积]
返回sum
对于这题目的数据来说时间复杂度肯定是不够的,我们要想办法优化它。。。
观察我们计算[T和当前点形成的矩形面积]时的方法:
假设当前点坐标是(x,y)
那么S=(t-x)*(t-y)
我们可以将上式展开:S=t*t-t(x+y)+xy
我们可不可以将上式分成的三部分分别求和呢?答案是可以的!
那么我们可以将所有矩形左下角和右上角的点分到一组a(因为它们和T形成的矩形面积都是做“加”运算),把左上角和右下角的点分到一组b(因为它们和T形成的矩形面积都是做“减”运算)
那么结果可以写成sigma[a中在(t,t)范围内的点和T形成的矩形面积]-sigma[b在(t,t)范围内的点和T形成的矩形面积]
很容易想到,我们将a,b中的点分别按max(x,y)排序。然后正确的算法已经呼之欲出了!
对于每次询问t,我们二分找到它在a,b中的位置n,m(即max(x,y)恰好不超过t的最大的下标,a,b都是从1开始编号)
答案不就是
Sum(Sa)-Sum(Sb)
=sigma[t*t-t*(x+y)+xy](a中点)-sigma[t*t-t*(x+y)+xy](b中点)
=[sigma(t*t)-sigma(x+y)+sigma(xy)](a中点)-[sigma(t*t)-sigma(x+y)+sigma(xy)](b中点)
计算sigma(t*t)只要t*t乘个数(对于a是n,对于b是m)即可!
计算sigma(x+y)和sigma(xy)只要预处理一下即可!
现在算法如下:
检查所有矩形的四个顶点
如果是左下角或是右上角的点那么放到a的末尾
否则放到b的末尾
将a,b中的所有点按max(x,y)排序
定义suma,sumb表示a、b的点中下标1到下标i的所有点的x+y和
定义suma_mul,sumb_mul表示a、b的点中下标1到下标i的所有点的x*y和
循环 i=1 到 2*N
suma[i]=suma[i-1]+a[i].x+a[i].y
sumb[i]=sumb[i-1]+b[i].x+b[i].y
suma_mul[i]=suma_mul[i-1]+a[i].x*a[i].y
sumb_mul[i]=sumb_mul[i-1]+b[i].y*b[i].y
对于每次询问t
二分找到在a,b中max(x,y)恰好不超过t的下标n,m
输出答案(t*t*n-t*suma[n]+suma_mum[n])-(t*t*m-t*sumb[m]+sumb_mul[m])
看过后敲代码不难。注意以后在涉及计算方面要把问题往数学公式方面靠近。
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#define LL __int64
using namespace std;
const int N= 20100;
struct Point{
int x,y,qc;
Point (){}
Point (int x1,int y1){
x=x1,y=y1;
qc=max(x,y);
}
}a[N*2],b[N*2];
int n;
LL aad[N*2],aam[N*2];
LL bad[N*2],bam[N*2];
bool cmp(Point a,Point b){
if(a.qc<b.qc ) return true;
return false;
}
int bin(Point *s,int t){
int l=0,r=2*n-1;
int ans=-1;
while(l<=r){
int m=(l+r)>>1;
if(s[m].qc<=t){
ans=m;
l=m+1;
}
else r=m-1;
}
return ans;
}
int main(){
int T,x1,y1,x2,y2,cnta,cntb,m,t;
scanf("%d",&T);
while(T--){
scanf("%d",&n);
cnta=cntb=0;
for(int i=0;i<n;i++){
scanf("%d%d%d%d",&x1,&y1,&x2,&y2);
a[cnta++]=Point(x1,y1);
a[cnta++]=Point(x2,y2);
b[cntb++]=Point(x1,y2);
b[cntb++]=Point(x2,y1);
}
sort(a,a+2*n,cmp);
sort(b,b+2*n,cmp);
aad[0]=a[0].x+a[0].y; aam[0]=a[0].x*a[0].y;
bad[0]=b[0].x+b[0].y; bam[0]=b[0].x*b[0].y;
for(int i=1;i<n*2;i++){
aad[i]=aad[i-1]+a[i].x+a[i].y;
aam[i]=aam[i-1]+(LL)a[i].x*(LL)a[i].y;
bad[i]=bad[i-1]+b[i].x+b[i].y;
bam[i]=bam[i-1]+(LL)b[i].x*(LL)b[i].y;
}
scanf("%d",&m);
LL ans;
while(m--){
scanf("%d",&t);
int a1=bin(a,t),b1=bin(b,t);
if(a1==-1)
puts("0");
else if(b1==-1){
ans=(LL)(a1+1)*(LL)t*(LL)t-aad[a1]*(LL)t+aam[a1];
printf("%I64d
",ans);
}
else{
ans=(LL)(a1+1)*(LL)t*(LL)t-aad[a1]*(LL)t+aam[a1]-((LL)(b1+1)*(LL)t*(LL)t-bad[b1]*(LL)t+bam[b1]);
printf("%I64d
",ans);
}
}
}
return 0;
}