插入排序
直接插入排序
每次将一个待排序的记录,按其关键字大小插入到前面的已经排好的子表中的适当的位置。直到全部记录插入完成为止。
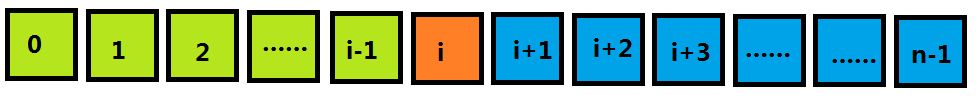
看图说话,如图所示:
一共有 N 个记录 ,放在 R 列表中 R[0,n-1]
在排序过程中的某一时刻,呈现了如果所示的场景。
其中:
浅绿色为 已经排好序的 部分 称之为 有序区 R[0,i-1]
橘色为 当前元素
橘色+ 蓝色 为尚未排序的 部分 称之为 无序区 R[i,n-1]
我们排序的时候,总是将无序区的第一个记录,放到有序区的合适位置,使有序区长度 +1 ,形成新的有序区 R[0,i]
说人话:
其实最开始的时候,我们就假设该列表的的有序区内仅含有一个记录。即列表的第一个记录 R[0]
其余所有记录都位于无序区,即R[1,n-1] 均为无序区。
开始排序:
从无序区拿第一个元素和有序区的最后一个元素比较,即R[1] 和R[0] 比较,如果 R[1] 小于R[0],那么R[0]向后移动一位,占据R[1]的位置。将原R[1] 插入到R[0] 前面。即原来R[0]的位置。有序区长度+1;如果R[1] 大于R[0],两个记录保持不变。有序区长度依旧+1。有序区编程R[0],R[1]
经过过上一步的比较、排序,现在的无序区的第一个记录就变成了R[2],然后将R[2] 提出来,依次和它前面的记录进行比较,如果发现比R[2]小的记录,那么将R[2]插入到该记录后面。假设一种情况:R[2] 首先和R[1]比较,发现R[2] 大于R[1] 于是将R[1]向后移动一位,注意:先别急着把R[2]插入到R[1]的前面。因为你不知道R[0]和R[2]的关系。所以,继续用R[2]和R[0]比较,假设R[0]小于R[2]了,那么这个时候,再将R[2]放入到R[0]的后面即R[1]的位置。
。。。。
直到所有的记录都这样插入一个遍。
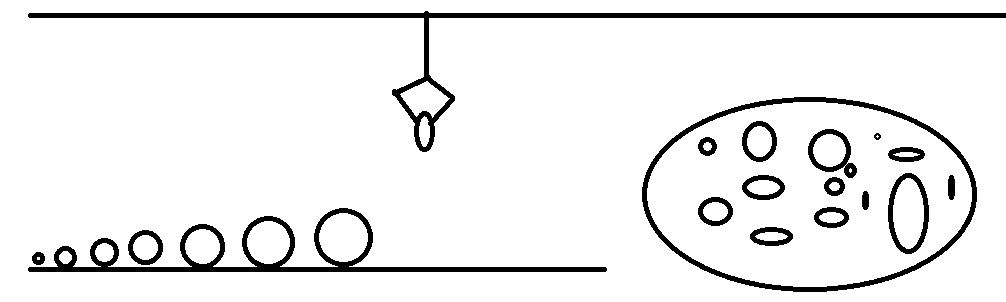
可以这样理解,有一个平台上,上面都是排列好的娃娃(左边一排排)。还有一对杂乱无章的娃娃(右侧圆圈),无乱的堆放在一起。你操作着头顶的机械手,每次从右边的那一大堆的娃娃里面夹起一个,然后向左移动。在平台上,每看到一个娃娃,那么就将机械手里夹着的娃娃和现在你看到的平台上的娃娃那个更大,如果发现平台上的娃娃更大,那么就继续向左移动机械手,看平台上下一个娃娃,如果还是平台上的娃娃大,那么继续向左移动机械手。。。知道你发现机械手的娃娃比平台上的那个娃娃大(假设叫 z ),那么就将机械手上的娃娃放到 z 的后面。其他的比你手里的娃娃大的那些娃娃,在你每一次比较完毕之后,都被人向右移动了一些距离。于是,刚好就给你流出了放置娃娃的空间。
代码如下:

def insert_sort(A): n = len(A) # 序列A 的长度 for i in range(1,n): # 从序列A 的第二个元素开始比较。即下标从 1 开始。 temp = A[i] # 设置一个变量,承接当前的 元素的值 j = i -1 # 有序区的最后一个元素的索引,每次比较都是从和该位置元素比较开始,逐渐向左推进。 while j>=0 and temp<A[j]: # j 指代 每个有序区元素的索引,所以j 不能小于0。 当 当前元素 小于 要比较的元素时,进行while循环。 A[j+1]=A[j] # 将比当前元素大的有序区的元素向右移动一个位置。 j -= 1 # 不着急放下当前元素,而是继续查看在j 元素之前是否还有元素,且该元素和当前元素相比,哪个大 A[j+1] = temp # j前面已经没有元素了,或者是那个元素小于当前元素。那么将当前元素放到那个元素的后面。 return A a = [34,1,4,3,6,8,89,23,12] print(insert_sort(a))
二、折半插入排序(二分插入排序)
直接插入排序是比较一下,移动一下记录的位置,再比较一下,再移动一次。。。。有点浪费时间。因此鉴于有序区已经有序这一特性,我们可以通过使用折半(二分)查找,快速找到要插入的位置,然后移动该位置以后的所有记录,将当前记录插入到目标位置。
代码如下:

def insert_into(A): n = len(A) for i in range(1,n): # 无序区从1到n-1 low = 0 #初始化 low ,最开始为0 heigh = i-1 #初始化 heigh ,最开始为 i-1 ,为有序区最大索引, temp = A[i] #定义一个变量,盛放无序区第一个元素,也就是要插入的元素 while low <= heigh: #开始二分查找。注意 low <= heigh 这个条件 mid = (low + heigh) // 2 # mid 是随着每次low或者是heigh的调整而动态调整的。且,为防止出现小数,故使用地板除 if temp < A[mid]: # 如果 当前元素小于列表的中间元素 heigh = mid - 1 # 移动heigh到mid-1位置。 以下同理,移动low的位置。直到出现low>heigh情况,退出循环 else: low = mid + 1 for j in range(i-1,heigh,-1): # 经过上述循环,找到要插入的位置即为heigh+1 ,因此从 i-1到heigh的元素都 统一向后移动。一会儿具体说为什么目标位置是 heigh+1 。 A[j+1] = A[j] A[heigh+1] = temp # 将当前元素放到相应位置。排序完成,返回序列。 return A abc =[34,1,4,3,6,8,89,23,12] print(insert_into(abc))
现在来说一说为什么要插入到 heigh+1 的位置。
其实当时犯晕也是因为二分查找没有学好。因此也就在详细分析分析
随着二分查找的进行,low / heigh的不断移动,会出现low和heigh出现两种情况:
1、low 和 heigh 是相邻元素
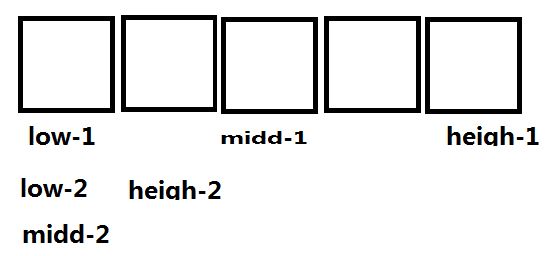
low_1, midd_1, heigh_1 是上一次查找的结果,
现在进行下一次查找 发现 temp小于midd_1 ,于是heigh 移动到midd_1-1的位置(midd_1前一位)。记作heigh_2
此时出现了low_2(还是原来的low-1位置,只是变了名字,表示有一次查找结果),和heigh_2 这种情况,即 low和heigh相邻。
此时又进行二分查找。midd_2即为low和heigh的中间元素,因为二分查找规定,和使用地板除,所以midd_2实际上是和low_2 处于同一的位置。
if temp>midd_2:
low = midd_2 +1 #情况一
else:
heigh = midd_2 -1 #情况二
情况一:
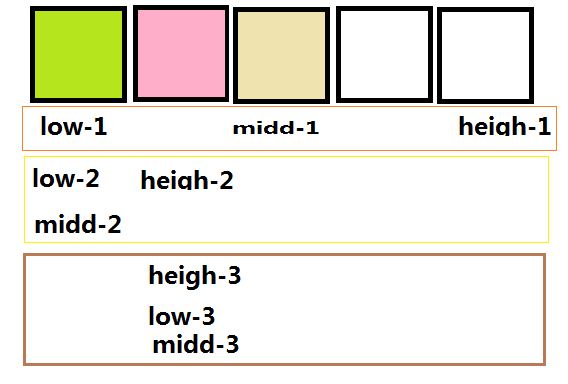
low_3 == heigh_3 即 low 和heigh位于同一个位置。此时符合更上一层二分查找的条件 low <= heigh 因此继续进行二分查找。
midd_3 = (low_3+heigh_3)//2 = heigh_3
此时:
如果temp > midd_3 也就是说temp > heigh_3 ==》》temp>heigh ,所以,heigh以后的元素都应该向右移动一个位置,“留出” heigh+1 来供 temp 使用
如果temp < midd_3 ,那么heigh = midd_3-1 。如下图:
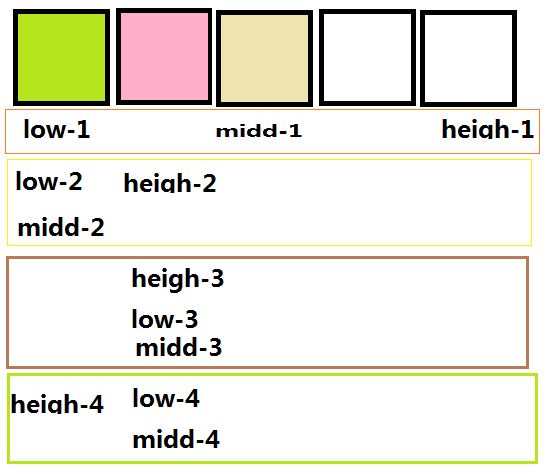
heigh_4 < low_4 即 low> heigh 退出二分查找
temp应该位于heigh_4+1的位置。即:low_4和midd_4的位置。即low的位置。
此时low = heigh+1
那么low及其以后的元素都应该向后移动过一个位置,留出low即 heigh+1 的位置来供temp使用
2、是low 和heigh位于同一个位置的时候
这种情况和heigh_3的情况一致
所以 heigh+1 即为要插入的位置。
