Java实现地理坐标判断

Java实现地理坐标判断

在做一个海洋相关的项目时候，遇到这个需求，判断船只是否在雷达监控的区域内，或者是否在某个保护区内。抽象为在地理位置中，一个坐标点是否在由一个圆心和半径的圆区域内，一个点是否在由一组点构成的区域内。

分析

多边形和圆分开写，首先简单的就是判断是否在圆里面，如何判断一个坐标是否在圆形区域内，相信不用我说都知道，计算这个坐标点和圆心之间的距离，然后跟圆的半径进行比较，如果比半径大，就不在圆形区域内，如果小于等于圆的半径，则该坐标点在圆形区域内。

点在圆区域内

数学上的计算公式是这样的：

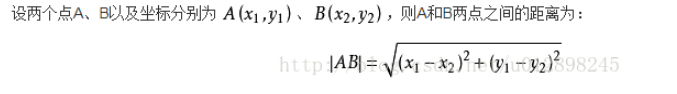
代码采用谷歌地图计算距离的方式，应该算是比较精确。

private static double EARTH_RADIUS = 6378.137;
 
    private static double rad(double d) {
        return d * Math.PI / 180.0;
    }
 
    /**
     * 通过经纬度获取距离(单位：米)
     *
     * @param lat1
     * @param lng1
     * @param lat2
     * @param lng2
     * @return
     */
    public static double getDistance(double lat1, double lng1, double lat2,
                                     double lng2) {
        double radLat1 = rad(lat1);
        double radLat2 = rad(lat2);
        double a = radLat1 - radLat2;
        double b = rad(lng1) - rad(lng2);
        double s = 2 * Math.asin(Math.sqrt(Math.pow(Math.sin(a / 2), 2) +
                Math.cos(radLat1) * Math.cos(radLat2) * Math.pow(Math.sin(b / 2), 2)));
        s = s * EARTH_RADIUS;
        s = Math.round(s * 10000d) / 10000d;
        return s;
    }
 
    /**
     * 判断一个点是否在圆形区域内
     */
    public static boolean isInCircle(double lng1, double lat1, double lng2, double lat2, String radius) {
        return getDistance(lat1, lng1, lat2, lng2) > Double.parseDouble(radius);
    }

如果使用Math.hypot()方法，计算(经纬度距离时)结果会有偏差）：

    double x = (lon1 - lon2) * PI * R * Math.cos(((lat1 + lat2) / 2) * PI / 180) / 180;
    double y = (lat1 - lat2) * PI * R / 180;
    double distance = Math.hypot(x, y);

点在多边形区域内

这里用到JAVA的关于坐标系和几何图形的一个类GeneralPath，使用这个类，结合传入的各顶点参数，画一个几何图形，并通过它自身的contains方法，判断一点是否在这个几何图形内。

也就是，通过JAVA已经封装好的方法，画一个几何多边形，判断一点是否在这个几何多边形里面。

/**
     * 判断是否在多边形区域内
     * 
     * @param pointLon
     *            要判断的点的纵坐标
     * @param pointLat
     *            要判断的点的横坐标
     * @param lon
     *            区域各顶点的纵坐标数组
     * @param lat
     *            区域各顶点的横坐标数组
     * @return
     */
    public static boolean isInPolygon(double pointLon, double pointLat, double[] lon,double[] lat) {
        // 将要判断的横纵坐标组成一个点
        Point2D.Double point = new Point2D.Double(pointLon, pointLat);
        // 将区域各顶点的横纵坐标放到一个点集合里面
        List<Point2D.Double> pointList = new ArrayList<Point2D.Double>();
        double polygonPoint_x = 0.0, polygonPoint_y = 0.0;
        for (int i = 0; i < lon.length; i++) {
            polygonPoint_x = lon[i];
            polygonPoint_y = lat[i];
            Point2D.Double polygonPoint = new Point2D.Double(polygonPoint_x, polygonPoint_y);
            pointList.add(polygonPoint);
        }
        return check(point, pointList);
    }
 
    /**
     * 一个点是否在多边形内
     * 
     * @param point
     *            要判断的点的横纵坐标
     * @param polygon
     *            组成的顶点坐标集合
     * @return
     */
    private static boolean check(Point2D.Double point, List<Point2D.Double> polygon) {
        java.awt.geom.GeneralPath peneralPath = new java.awt.geom.GeneralPath();
 
        Point2D.Double first = polygon.get(0);
        // 通过移动到指定坐标（以双精度指定），将一个点添加到路径中
        peneralPath.moveTo(first.x, first.y);
        polygon.remove(0);
        for (Point2D.Double d : polygon) {
            // 通过绘制一条从当前坐标到新指定坐标（以双精度指定）的直线，将一个点添加到路径中。
            peneralPath.lineTo(d.x, d.y);
        }
        // 将几何多边形封闭
        peneralPath.lineTo(first.x, first.y);
        peneralPath.closePath();
        // 测试指定的 Point2D 是否在 Shape 的边界内。
        return peneralPath.contains(point);
    }

点在多边形区域内（简单版）

先将横纵坐标数组的横坐标最大最小值，纵坐标的最大最小值，求出来，需要判断的一点大于横纵坐标的最大值或者小于横纵坐标的最小值，也就是粗略的计算一下，如果这个条件不满足的话，就不用往下计算了，直接不在指定的区域里面。

/**
     * 判断该地理坐标是否在最大范围区域内
     * 
     * @param pointLon
     *            要判断的点的纵坐标
     * @param pointLat
     *            要判断的点的横坐标
     * @param lon
     *            指定区域的纵坐标组成的数组
     * @param lat
     *            指定区域的横坐标组成的数组
     * @return
     */
    private static boolean isInMaxArea(double pointLon, double pointLat, double[] lon,
            double[] lat) {
 
        // 获取区域横纵坐标最大值和最小值
        double temp = 0.0;
        for (int i = 0; i < lon.length; i++) {
            for (int j = 0; j < lon.length - i - 1; j++) {
                if (lon[j] > lon[j + 1]) {
                    temp = lon[j];
                    lon[j] = lon[j + 1];
                    lon[j + 1] = temp;
                }
            }
        }
        for (int i = 0; i < lat.length; i++) {
            for (int j = 0; j < lat.length - i - 1; j++) {
                if (lat[j] > lat[j + 1]) {
                    temp = lat[j];
                    lat[j] = lat[j + 1];
                    lat[j + 1] = temp;
                }
            }
        }
 
        // 如果在最值组成的区域外，那肯定不在重点区域内
        return (pointLon < lon[0] || pointLon > lon[lon.length - 1] || pointLat < lat[0]
                || pointLat > lat[lat.length - 1]);
    }

如果通过了上面的判断，可以进行接下来的算法判断了

用到了两点间的斜率公式

这个方法就是，通过一点，画一条线，这条线与多边形相交，如果相交点数位奇数，就在区域内，如果为偶数，就不在区域内

代码：

/**
     * 判断坐标是否在重点区域内
     * 
     * @param pointLon
     *            要判断的点的纵坐标
     * @param pointLat
     *            要判断的点的横坐标
     * @param lon
     *            指定区域的纵坐标组成的数组
     * @param lat
     *            指定区域的横坐标组成的数组
     * @return
     */
    private static boolean isInAccurateArea(double pointLon, double pointLat, double[] lon,
            double[] lat) {
        // 代表有几个点
        int vertexNum = lon.length;
        boolean result = false;
        
        for (int i = 0, j = vertexNum - 1; i < vertexNum; j = i++) {
            // 满足条件，与多边形相交一次，result布尔值取反一次，奇数个则在区域内
            if ((lon[i] > pointLon) != (lon[j] > pointLon)
                    && (pointLat < (lat[j] - lat[i]) * (pointLon - lon[i]) / (lon[j] - lon[i])
                            + lat[i])) {
                result = !result;
            }
        }
        return result;
    }

参考博客：https://blog.csdn.net/u012898245/article/details/79450433