Given an array nums containing n + 1 integers where each integer is between 1 and n (inclusive), prove that at least one duplicate number must exist. Assume that there is only one duplicate number, find the duplicate one.
Note:
- You must not modify the array (assume the array is read only).
- You must use only constant, O(1) extra space.
- Your runtime complexity should be less than
O(n2). - There is only one duplicate number in the array, but it could be repeated more than once.
题目标签:Array, Binary Search, Two Pointers
题目给了我们一个nums array, 让我们找到其中的重复数字。因为这一题有4个条件,所以有难度。1. 要求我们不能改动array;2. 只能用O(1)空间;3. 时间要小于O(n^2);4. 只有一个重复的数字,但是它可以出现最少1次。
方法1:O(logn * n)
利用binary search。
题目给的数字是在 [1, n] 之间, array 的size 是 n+1。所以肯定有一个数字会至少出现2次。
分析一下:
如果n 是5,那么就会有1 2 3 4 5 一共5个数字的可能,而array size 是6,那么其中一个数字肯定会至少出现两次。
如果没有重复的数字,小于等于1的数字 出现的次数 等于 1;
小于等于2的数字 出现的次数 等于 2;
... 同理3;4;5。
如果有重复的数字,如果重复的是1,那么 小于等于1的数字 出现的次数 肯定大于1;
基于这个理论,我们可以在1 2 3 4 5 选出一个 mid, 遍历array来count 小于等于mid 的数字个数 小于等于 它自己mid 还是 大于 mid?
如果count 小于等于mid, 说明 1 到 mid 这些数字 没有重复项, 重复项在 右半边 mid 到n, 所以缩小到右半边继续搜索;
如果count 大于mid, 说明 1 到 mid 这些数字中 有重复项,缩小到 左半边继续搜索。
Java Solution:
Runtime beats 28.13%
完成日期:09/13/2017
关键词:Array, Binary Search
关键点:如果从1到n中 有重复项,那么必然有一个数字出现的次数至少是2次
1 class Solution 2 { 3 public int findDuplicate(int[] nums) 4 { 5 /* Solution 1: binary search */ 6 int low = 1, high = nums.length - 1; 7 8 while(low <= high) 9 { 10 int mid = low + (high - low) / 2; 11 int cnt = 0; 12 13 for(int a: nums) 14 { 15 if(a <= mid) 16 cnt++; 17 } 18 19 if(cnt <= mid) // meaning duplicate is on the right side 20 low = mid + 1; 21 else // if cnt > mid, meaning duplicate is on the left side 22 high = mid - 1; 23 24 } 25 26 return low; 27 } 28 }
参考资料:
http://bookshadow.com/weblog/2015/09/28/leetcode-find-duplicate-number/
方法2:O(n),利用slow 和fast 双指针,这个方法太巧妙了,有好几个点比较难理解。
利用slow 和 fast 指针,经历两次 相遇,来找到重复的数字。
相遇1: slow 一次走一步;fast 一次走两步。
当它们相遇的时候,让slow 保留在相遇的点上。
相遇2:让fast 从起点开始走,一次走一步;slow 在上一次相遇的点上开始走,一次走一步。
当它们相遇的时候,相遇的点就是重复的数字。
如何让slow fast 走步呢,利用slow = nums[slow]; fast = nums[nums[fast]]. 把index 所指的数字值 替换index 来模仿走步数。
来结合图片分析几个关键点:
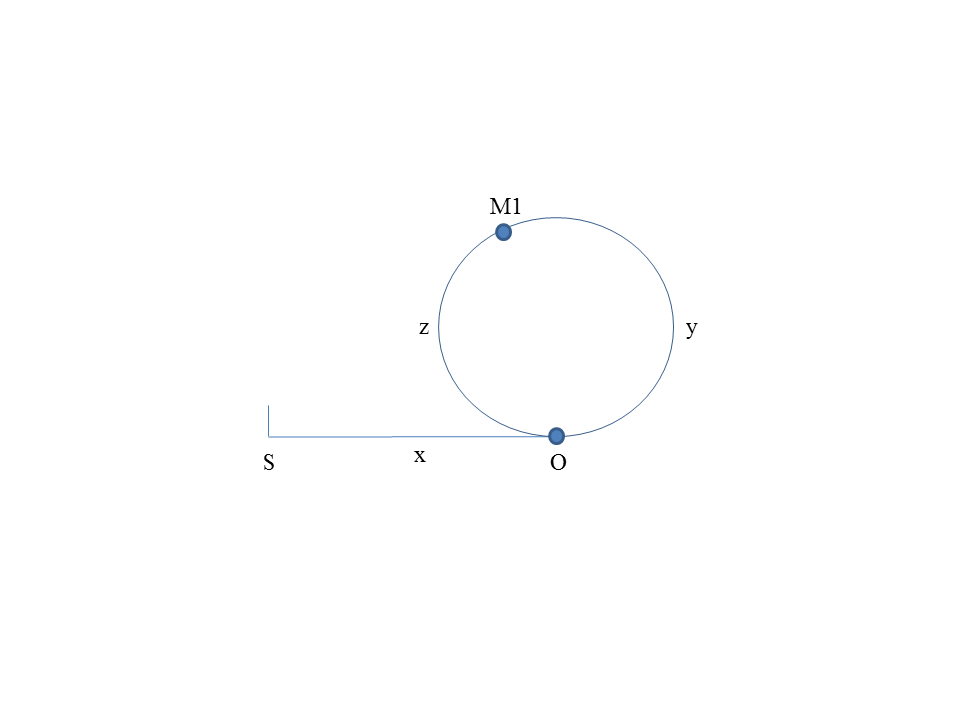
S 为起始点,O 为圆的入口,M1 为第一次相遇的地方,x 为S到O的长度, y 为 O到M1的长度, z 为 M1到O的长度。
1. 第一次相遇是为了找到它们的相遇点, 第二次相遇是为了找到圆的入口 O。
2. 路程会有一段path 接着和一个circle:
举例子来看一下:
0 1 2 3 4 5 6 7
[4,6,2,1,7,1,3,5]
n = 7, 数字都是 1 ~ 7 中的选择, array size = 8, 肯定会有一个数字,至少出现2次。
按照我们的方法来走一下:0 -> 4 -> 7 -> 5 -> 1 -> 6 -> 3 -> 1 -> 6 -> 3 -> 1 -> 6 -> 3 -> 1 ... 一直重复 1 6 3
红色部分可以看作为S - O path; 绿色部分可以看作为 O点; 蓝色部分看作为 圆。
3. 为什么会有一段path:
因为数字只能是 1 到 n, 所以index 0 肯定只能走过一次, 那么肯定有一段path, path 长度得看情况。
4. 为什么会有一个circle:
因为index 除了0, 有1到n(而且唯一不重复); 数字也是1到n, 所以每一次 index 指向数字 时候, 那个数字肯定能成为新的和唯一的 index,一直循环。
5. 为什么O 点一定是 重复的那个数字?
我们来看之前的例子: index array 里,红色的两列是重复的数字。3 能走到 1, 5 也能走到1, 3和5 代表着两条路,所以当两条路汇合的地方,就是重复的数字1。
6. 为什么x = z?
换句话说,为什么第二次它们能够相遇。这应该是最麻烦的地方。
方法1: 验证一下
第一次相遇后: slow 走的路程 = x + y;fast 走的路程 = x + y + z + y;fast = x + 2y + z。
因为第一次是slow 走一步,fast 走两步,所以 2slow = fast。
代入公式:2x + 2y = x + 2y + z
x = z
方法2:我们想象一下,
情况1:如果slow 和fast 都从O点出发,slow 一次走一步,fast 一次走两步,那么当它们相遇的时候,slow 走了一圈,fast 走了两圈,而且它们一定相遇在O点;(可以在图上画刻度,自己走走看)
情况2:如果我们多加一段path, 让它们从S点出发,slow 一次走一步,fast 一次走两步, 那么它们什么时候能相遇呢? 情况1中它们相遇在O点,那么多加一段path(x 是path的长度),它们会在O点的基础上,提早x 的距离相遇,因为它们多走了一段x的path,所以fast 会在O之前就赶上slow。所以 x 肯定等于 z。
7. 如果不太明白的话,可以画一个类似的图,再画上刻度,自己多走几次,感受一下。
Java Solution:
Runtime beats 51.39%
完成日期:09/14/2017
关键词:Array, Two Pointers
关键点:快慢指针相遇的点就是重复的数字
1 class Solution 2 { 3 public int findDuplicate(int[] nums) 4 { 5 /* Solution 2: */ 6 int slow = 0, fast = 0; 7 // fist meeting 8 do 9 { 10 slow = nums[slow]; // slow takes one step each time 11 fast = nums[nums[fast]]; // fast takes two steps each time 12 13 }while(slow != fast); 14 15 // second meeting 16 fast = 0; 17 18 while(slow != fast) 19 { 20 slow = nums[slow]; // both slow and fast take one step each time 21 fast = nums[fast]; 22 } 23 // when they meet, the place must be entry of circle, and must be duplicate 24 return slow; 25 } 26 }
参考资料:
http://blog.csdn.net/monkeyduck/article/details/50439840
LeetCode 题目列表 - LeetCode Questions List