12.29 76. 剪绳子
给你一根长度为 n 的绳子,请把绳子剪成整数长度的 m 段(m、n都是整数,n>1并且m>1),每段绳子的长度记为 k[0],k[1]...k[m-1] 。请问 k[0]k[1]...*k[m-1] 可能的最大乘积是多少?例如,当绳子的长度是8时,我们把它剪成长度分别为2、3、3的三段,此时得到的最大乘积是18。
输入: 10
输出: 36
解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36
最优解思路
动态规划:
对于的正整数 n,当 n≥2 时,可以拆分成至少两个正整数的和。令 k 是拆分出的第一个正整数,则剩下的部分是 n−k,n−k 可以不继续拆分,或者继续拆分成至少两个正整数的和。由于每个正整数对应的最大乘积取决于比它小的正整数对应的最大乘积,因此可以使用动态规划求解。
dp数组的含义: dp[i] 表示将正整数 i 拆分成至少两个正整数的和之后,这些正整数的最大乘积。
边界条件: 0 不是正整数,1 是最小的正整数,0 和 1 都不能拆分,因此 dp[0]=dp[1]=0。
状态转移方程:
当 i≥2 时,假设对正整数 i 拆分出的第一个正整数是 j(1≤j<i),则有以下两种方案:
将 i 拆分成 j 和 i−j 的和,且 i−j 不再拆分成多个正整数,此时的乘积是 j×(i−j);
将 i 拆分成 j 和 i−j 的和,且 i−j 继续拆分成多个正整数,此时的乘积是 j×dp[i−j]。
因此,当 j 固定时,有 dp[i]=max(j×(i−j),j×dp[i−j])。由于 j 的取值范围是 1 到 i−1,需要遍历所有的 j 得到 dp[i] 的最大值,因此可以得到状态转移方程如下:
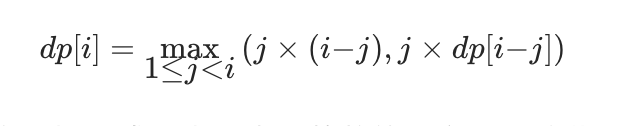
最优解
class Solution {
public int cuttingRope(int n) {
int[] dp = new int[n + 1];
for (int i = 2; i <= n; i++) {
for (int j = 1; j < i; j++) {
dp[i]= Math.max(dp[i], Math.max(j * (i - j), j * dp[i - j]));
}
}
return dp[n];
}
}
最优解总结
相当于求出d0,d1,d2....dn, 每次都要依赖之前的结果。
12.30 77. 组合总和
给定一个由正整数组成且不存在重复数字的数组,找出和为给定目标正整数的组合的个数。
nums = [1, 2, 3]
target = 4
所有可能的组合为:
(1, 1, 1, 1)
(1, 1, 2)
(1, 2, 1)
(1, 3)
(2, 1, 1)
(2, 2)
(3, 1)
请注意,顺序不同的序列被视作不同的组合。
因此输出为 7。
最优解思路
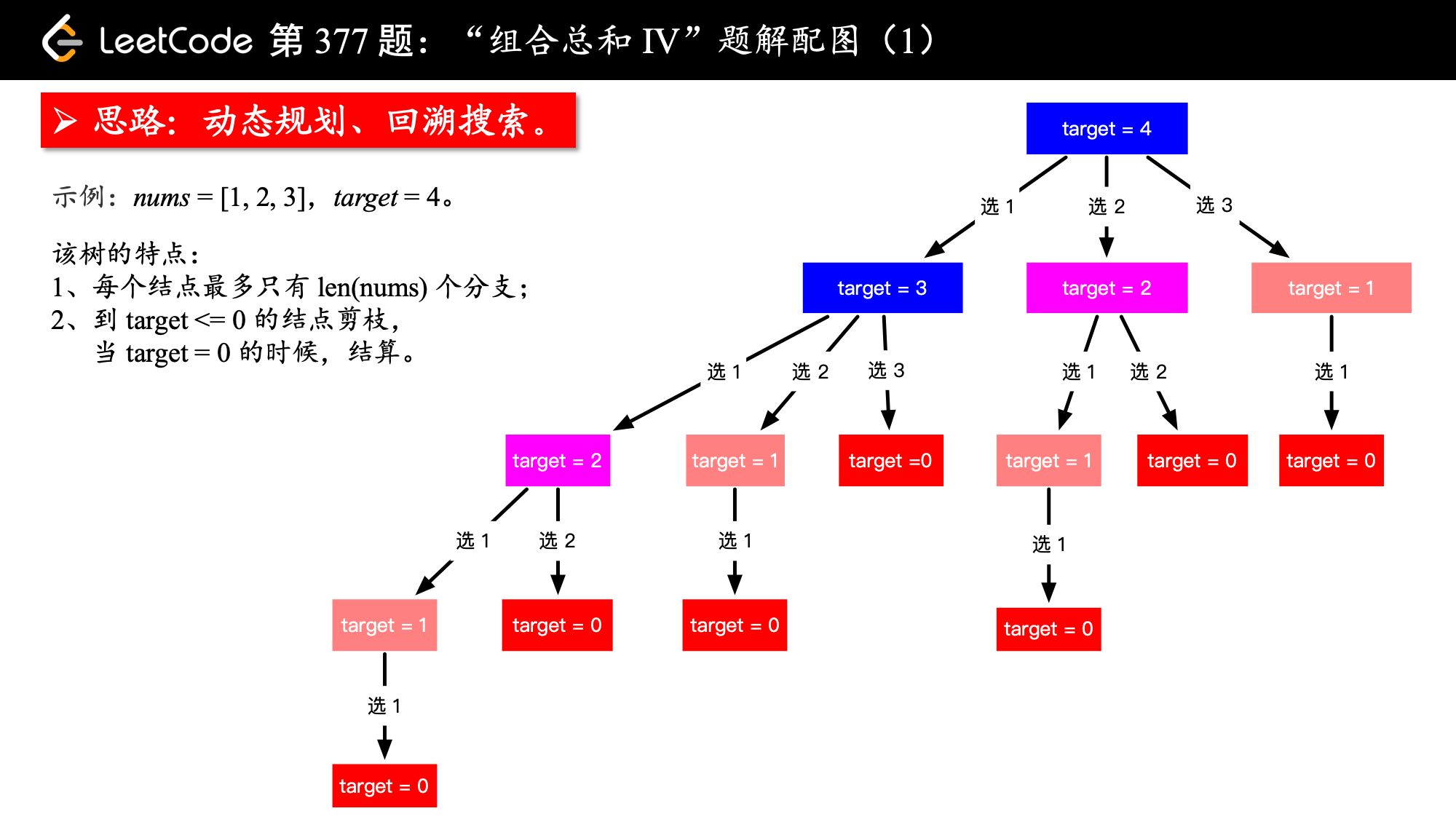
“动态规划”的两个步骤是思考“状态”以及“状态转移方程”。
1、状态
对于“状态”,我们首先思考能不能就用问题当中问的方式定义状态,上面递归树都画出来了。当然就用问题问的方式。
dp[i] :对于给定的由正整数组成且不存在重复数字的数组,和为 i 的组合的个数。
思考输出什么?因为状态就是问题当中问的方式而定义的,因此输出就是最后一个状态 dp[n]。
2、状态转移方程
由上面的树形图,可以很容易地写出状态转移方程:
dp[i] = sum{dp[i - num] for num in nums and if i >= num}
注意:在 0 这一点,我们定义 dp[0] = 1 的,它表示如果 nums 里有一个数恰好等于 target,它单独成为 1 种可能。
最优解
class Solution:
def combinationSum4(self, nums, target):
size = len(nums)
if size == 0 or target <= 0:
return 0
dp = [0 for _ in range(target + 1)]
# 这一步很关键,想想为什么 dp[0] 是 1
# 因为 0 表示空集,空集和它"前面"的元素凑成一种解法,所以是 1
# 这个值被其它状态参考,设置为 1 是合理的
dp[0] = 1
for i in range(1, target + 1):
for j in range(size):
if i >= nums[j]:
dp[i] += dp[i - nums[j]]
return dp[-1]
最优解总结
dp[4] = 1+dp[3] 的 数量 加 2+dp[2]的数量 加3+dp[1]的数量,即dp[1]+dp[2]+dp[3],同理,分解其中的每一项所以要判断,
for num in nums:
if i >= num:
只能由比他小的数字构成。一共有0,1,2,到target,所以是target+1项,每一项都会有对应的组合数量。
12.31 78. 目标和
给定一个非负整数数组,a1, a2, ..., an, 和一个目标数,S。现在你有两个符号 + 和 -。对于数组中的任意一个整数,你都可以从 + 或 -中选择一个符号添加在前面。
返回可以使最终数组和为目标数 S 的所有添加符号的方法数。
输入:nums: [1, 1, 1, 1, 1], S: 3
输出:5
解释:
-1+1+1+1+1 = 3
+1-1+1+1+1 = 3
+1+1-1+1+1 = 3
+1+1+1-1+1 = 3
+1+1+1+1-1 = 3
一共有5种方法让最终目标和为3。
最优解思路
我们用 dp[i][j] 表示用数组中的前 i 个元素,组成和为 j 的方案数。考虑第 i 个数 nums[i],它可以被添加 + 或 -,因此状态转移方程如下:
dp[i][j] = dp[i - 1][j - nums[i]] + dp[i - 1][j + nums[i]]
由于数组中所有数的和不超过 1000,那么 j 的最小值可以达到 -1000。在很多语言中,是不允许数组的下标为负数的,因此我们需要给 dp[i][j] 的第二维预先增加 1000,即:
dp[i][j + nums[i] + 1000] += dp[i - 1][j + 1000]
dp[i][j - nums[i] + 1000] += dp[i - 1][j + 1000]
最优解
public class Solution {
public int findTargetSumWays(int[] nums, int S) {
int[][] dp = new int[nums.length][2001];
dp[0][nums[0] + 1000] = 1;
dp[0][-nums[0] + 1000] += 1;
for (int i = 1; i < nums.length; i++) {
for (int sum = -1000; sum <= 1000; sum++) {
if (dp[i - 1][sum + 1000] > 0) {
dp[i][sum + nums[i] + 1000] += dp[i - 1][sum + 1000];
dp[i][sum - nums[i] + 1000] += dp[i - 1][sum + 1000];
}
}
}
return S > 1000 ? 0 : dp[nums.length - 1][S + 1000];
}
}
2021
1.1 79. 零钱兑换
给定不同面额的硬币和一个总金额。写出函数来计算可以凑成总金额的硬币组合数。假设每一种面额的硬币有无限个。
输入: amount = 5, coins = [1, 2, 5]
输出: 4
解释: 有四种方式可以凑成总金额:
5=5
5=2+2+1
5=2+1+1+1
5=1+1+1+1+1
思路
类似于77组合总和,dp[n] 表示和为n的组合总数。但是注意重复的只算一种
最优解
class Solution:
@classmethod
def change(self, amount: int, coins: list) -> int:
if amount == 0:
return 0
dp = [0] * (amount + 1)
dp[0] = 1
for coin in coins:
for i in range(coin, amount + 1):
dp[i] += dp[i - coin]
return dp[amount]
1.2 80. 单词拆分
给定一个非空字符串 s 和一个包含非空单词的列表 wordDict,判定 s 是否可以被空格拆分为一个或多个在字典中出现的单词。
输入: s = "leetcode", wordDict = ["leet", "code"]
输出: true
解释: 返回 true 因为 "leetcode" 可以被拆分成 "leet code"。
输入: s = "catsandog", wordDict = ["cats", "dog", "sand", "and", "cat"]
输出: false
最优解思路
背包问题,动态规划。dp[i]表示s的前i位是否可以用wordDict中的单词表示。
遍历字符串的所有子串,开始索引i,区间为[0,n),结束索引j,区间为[i+1,n+1)
若dp[i] = True,且s[i,..j)在wordlist中:dp[j] = True。
最优解
class Solution:
def wordBreak(self, s: str, wordDict: List[str]) -> bool:
n=len(s)
dp=[False]*(n+1)
dp[0]=True
for i in range(n):
for j in range(i+1,n+1):
if(dp[i] and (s[i:j] in wordDict)):
dp[j]=True
return dp[-1]