罗德里格斯(Rodrigues)旋转方程
此公式有2种形式,故而也有2种推导方法。具体的推导过程如下
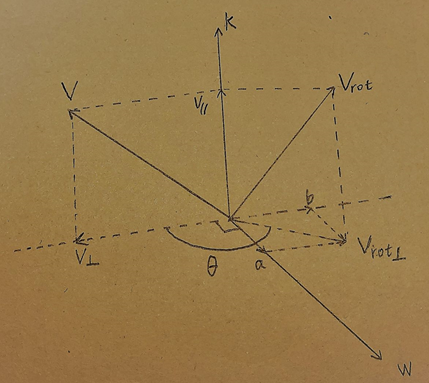
一、条件
定义向量k是旋转轴的单位矢量,图中初始向量v绕k轴旋转Θ角得vrot
二、说明
所谓推导旋转方程,实则求出一个旋转矩阵R,使得vrot=Rv。所以我们要做的就是找出vrot与v之间的关系,并用矩阵来表示。
三、推导
1. 推导一
对v进行向量分解: v = v⊥+ v//
由点乘的投影几何意义可得: v// = (v • k)k (v•k为标量,所以再乘k得到一个矢量)
根据向量减法可得: v⊥= v - v//
由旋转过程平行向量不变得: vrot //= v//
为计算方便,对vrot⊥进行向量分解:vrot⊥=a+b
由图中的向量关系经推导可得:b= cosΘ v⊥ a=sinΘ k x v (推导在文章末尾)
综上可得:vrot = vrot⊥+vrot //
= a + b + v//
= sinΘ k x v + cosΘ v⊥ + (v • k)k
= sinΘ k x v + cosΘ (v - v//)+ (v • k)k
= sinΘ k x v + cosΘ (v - (v • k)k)+ (v • k)k
= cosΘ v + (1 - cosΘ )(v • k)k + sinΘ k x v
显然:到此步,我们还无法将其用矩阵来表示,所以需要对 (v • k)k 和 k x v 进行矩阵转换
由结合律和点乘的交换律得(v • k)k=k •(v • k)=k • (kτ • v)=k•kτ•v ,其中的向量都是列向量
对于k x v可用叉乘矩阵来化简为Kv
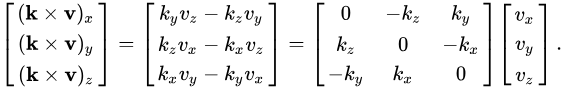
所以,cosΘ v + (1 - cosΘ )(v • k)k + sinΘ k x v
= cosΘ v + (1 - cosΘ )kkτv + sinΘKv
=( cosΘ I + (1 - cosΘ )kkτ + sinΘK ) v
=Rv
所以,旋转矩阵R=cosΘ I + (1 - cosΘ )kkτ + sinΘK,其中I为单位矩阵。
2.推导二
与推导一相比,推导二的不同主要在于用叉乘去表示一些数据
用叉乘来表示v⊥可得:v⊥= -k x (k x v)
所以联立推导一中各式得: vrot = vrot⊥+ vrot //
= a + b + v//
= sinΘ k x v + cosΘ v⊥ + v - v⊥
= sinΘ k x v - cosΘk x (k x v) + v + k x (k x v)
= v + (1 - cosΘ)k x (k x v) + sinΘ k x v
= v + (1 - cosΘ)K2v + sinΘ Kv (叉乘矩阵表示)
=(I + (1 - cosΘ)K2 + sinΘ K) v
=Rv
从而得出第二种表达式R=I + (1 - cosΘ)K2 + sinΘ K
显然,第二种表达式更为简便,在计算的过程中涉及的参数更少,所以这也是在进行旋转操作时常用的公式。
关于a和b的推导

a和b是由Vrot⊥正交分解得到的矢量,既有大小又有方向,所以在求解时,我们要对其大小和方向分别求解。
一、b的求解
1.大小
由图得:|b| = cosΘ' |Vrot⊥| ( Θ'为b和Vrot⊥的夹角 )
又因为|Vrot⊥| = |V⊥| ,Θ'=PI - Θ
所以:|b| = cos(PI - Θ) |V⊥| = (- cosΘ)|V⊥|
2.方向
由b的方向与V⊥方向相反可得
b的单位方向向量为:-V⊥ / |V⊥|
综上可得:b= (-V⊥ / |V⊥| ) |b| = cosΘV⊥
二、a的求解
1.大小
|a| = sinΘ' |Vrot⊥| = sinΘ' |V⊥| = sin(PI-Θ) |V⊥| = sinΘ|V⊥|
= sinΘsinΘ''|V| (Θ''为V和k的夹角)
= sinΘsinΘ''|V| |K| (因为 |K|=1,所以可直接加上)
其中sinΘ''|V| |K| = |K x V|
所以:|a| = sinΘ |K x V|
2.方向
由叉乘方向可得a的单位方向向量为
K x V / |K x V|
综上可得:a=(K x V / |K x V|) sinΘ |K x V| = sinΘ K x V