总目录 > 2 算法基础 > 2.6 倍增思想
前言
倍增通常和二分一起介绍,共同点在于——它们都能神奇地将原本复杂度为 n 的过程下降到 log n,对于大型数据而言,这种效率的提高是显而易见的。
子目录列表
1、二进制与倍增
2、例题
3、应用
2.6 倍增思想
1、二进制与倍增
众所周知,二进制与十进制转换关系:o = 2 ^ a * + 2 ^ b + ... + 2 ^ i,比如 77 = 2 ^ 6 + 2 ^ 3 + 2 ^ 2 + 2 ^ 0,则其二进制表示为 1001101。换言之,任何一个整数都可以由若干个系数为 1,x 为 2 的 2 次方幂的和组成。
所以尤记得小学时有个比较经典的问题:
如何用尽可能少的砝码称量出 [1, 30] 之间的所有重量?(天平左侧放物品右侧放砝码)
根据上述原理,则只需要 1, 2, 4, 8, 16 五个重量级的砝码即可,能够组成 [1, 30] 之间的任意数。
如果修改成 [1, 60] 呢?多一个 32 即可;
如果修改成 [1, 21647483647] 呢?则再加上 2 ^ 6, 2 ^ 7, ..., 2 ^ 30,总共也只需要 31 个砝码。
注意到,我们将这个看似巨大的数字,通过这个思路,很轻松地就得到了 log n 级别的一个结果。而倍增思想,字面意思就是翻倍,其实就是建立在二进制和十进制这个关系上的。
2、例题
给出一个长度为 n 的环和一个常数 k,每次可以从第 i 个点跳到第 (i + k) mod (n + 1) 个点,总共跳 m 次。第 i 个点的权值为 a[i],求 m 次跳跃的起点的权值之和 mod 1e9 + 7。
(原题面没有给出初始位置?)
强调一下数据范围:m <= 1e18,也就是说我们不可能对于每一次跳跃都记录位置。由于只需要知道 m 次跳跃的权值和,过程其实并不重要,那么就可以采用倍增的方式。
假设 n = 5, m = 29,将环拆成线性的。下图为跳跃图解:
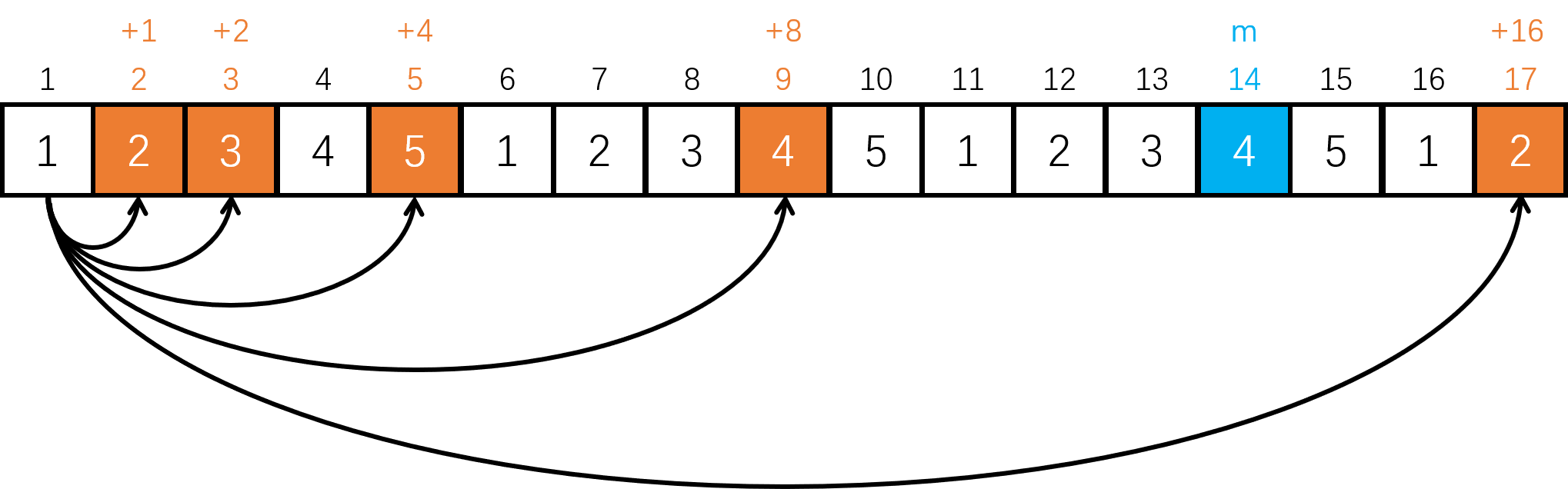
选择在终点之前最远的跳跃方式:从第 1 个位置跳到第 9 个位置。

从第 9 个位置跳到第 13 个位置。
最后从第 13 个位置跳到第 14 个位置,图略。
所以从 1 到 14 的整个跳跃过程由 2 ^ 3 + 2 ^ 2 + 2 ^ 0 三步组成。也就是说,对于环上这 n 个位置,预处理出每一个位置向前跳 1, 2, 4, ... 次的位置,则必然能够到达 m。1e18 <= 2 ^ 64,至多倍增跳跃 64 次就够了,而预处理过程同样只需要 O(n log m) 的时间/空间复杂度。
代码略。
3、应用
倍增思想最常见的应用:快速幂,LCA 和 RMQ 问题等等。
快速幂请参见:6.2 快速幂
倍增 LCA 请参见:<施工中>
RMQ 问题请参见:<施工中>