1、前言
考得稀下的,算了不说了。
2、Password 博士的密码
大概题意:给出一个数列,选出其中一些数字使其和为所给数字。
总结:被这道题坑死了!为了省时间,我事先排了序并且用了前缀和优化,但是它的数列存在负数,而且是所有数据都有负数,所以直接爆零无话可说。后来再看了一眼题目发现好像确确实实没有说一定是正整数。
题解:题解是非常鬼畜的。说先前60%直接暴力DFS即可(妈蛋);然后注意100分为n<=40。暴力显然是O(n!)的,所以当n>25时,我们可以把n个数分成两个部分,首先暴力算出两个部分的所有组合情况,然后利用两部分求和,使两部分总和满足条件。
3、Circle 套圈游戏
大概题意:地图上有一些点,给出一个两直角边长度已知的直角三角形,用直角三角形框住最多的点,要求直角点必须在地图上的点上。
总结:有没有看清题目,我觉得我可以弃疗了。三角形的直角必定在整数点上,所以对于40%数据直接O(n^2)枚举所有点就行了。呵呵。
题解:40分在上面。100分的话,CDQ分治省略,来讲讲容斥原理。根据题意易得我们是需要选择一个直角三角形,可以考虑将其三条边延长为直线,由此将坐标系划分成7个部分。学过线性规划的应该都知道怎么求第1部分面积;再根据容斥原理,易得S1=Sall-S(2,3,4)-S(2,7,6)-S(4,5,6)+S2+S6。如图:
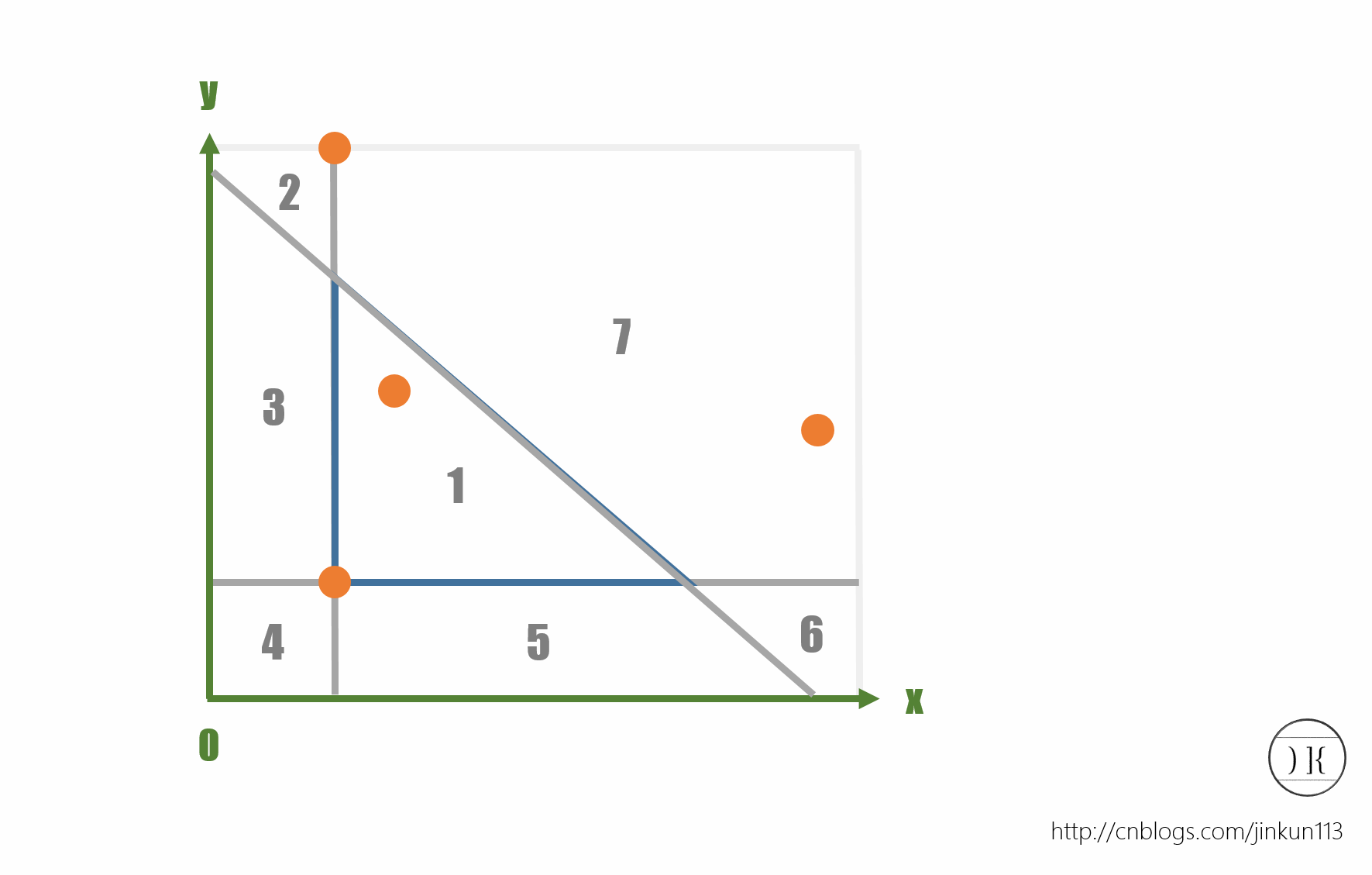
具体过程的话,如何判断一个点在一条线的那一侧?利用截距来判断简便而有效。求出Sall,S(2,3,4),S(2,7,6)和S(4,5,6)都是不难的,那么对于S2,S6,需要用树状数组来维护。
4、Last 最后一题
这道题不怎么想讲。。。。我题目其实看了很久才看懂,但是其实就是一道简单的数学题,但是由于数据范围极大<=10^500,所以麻烦的地方就是需要用到高精度加减乘法。另外奇偶性要考虑。