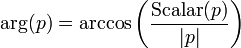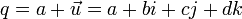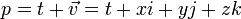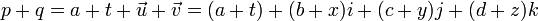zoukankan      html  css  js  c++  java

  • 四元数运算

    四元数运算[编辑]

    四元数运算在电动力学与广义相对论中有广泛的应用。四元数可以用来取代张量表示。有时候采用带有复数元素之四元数会比较容易，导得结果不为除法代数之形式。然而亦可结合共轭运算以达到相同的运算结果。

    此处仅讨论具有实数元素之四元数，并将以两种形式来描述四元数。其中一种是向量与标量的结合，另一形式两个创建量(constructor)与双向量(bivector；i、j与k)的结合。

    定义两个四元数:

    q = a + vec{u} = a + bi + cj + dk
    p = t + vec{v} = t + xi + yj + zk

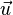    其中vec{u}表示矢量<b, c, d>，而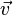vec{v}表示矢量<x, y, z>.

    加、乘和一般函数[编辑]

    四元数加法：p + q
    跟复数、向量和矩阵一样，两个四元数之和需要将不同的元素加起来：
    p + q = a + t + vec{u} + vec{v} = (a + t) + (b + x)i + (c + y)j + (d + z)k

    加法遵循实数和复数的所有交换律和结合律。

    四元数乘法：pq
    两个四元数之间的非可换乘积通常被称为格拉斯曼积，这个积上面已经简单介绍过，它的完整型态是：

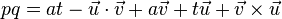
    pq = at -vec{u}cdotvec{v} + avec{v} + tvec{u} + vec{v} imesvec{u}

    pq = (at - bx - cy - dz) + (bt + ax + dy - cz)i + (ct + ay + bz - dx)j + (dt + za + cx - by)k \,

    由于四元数乘法的非可换性，pq并不等于qp。格拉斯曼积常用在描述许多其他代数函数。qp乘积的向量部分是:

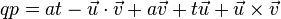
    qp = at -vec{u}cdotvec{v} + avec{v} + tvec{u} + vec{u} imesvec{v}

    四元数点积： p · q
    点积也叫做欧几里得内积，四元数的点积等同于一个四维向量的点积。点积的值是p中每个元素的数值与q中相应元素的数值的乘积的和。这是四元数之间的可换积，并返回一个标量。

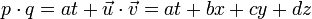
    p cdot q = at + vec{u}cdotvec{v} = at + bx + cy + dz

    点积可以用格拉斯曼积的形式表示:

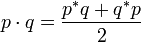
    p cdot q = frac{p^*q + q^*p}{2}

    这个积对于从四元数分离出一个元素有用。例如，i项可以从p中这样提出来：

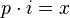
    p cdot i = x

    四元数外积：Outer(p,q) 

    欧几里得外积并不常用; 然而因为外积和内积的格拉斯曼积形式的相似性.它们总是一同被提及:

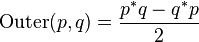
    operatorname{Outer}(p,q) = frac{p^*q - q^*p}{2}

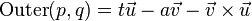
    operatorname{Outer}(p,q) = tvec{u} - avec{v} - vec{v} imesvec{u}

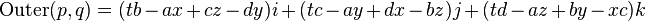
    operatorname{Outer}(p,q) = (tb - ax + cz - dy)i + (tc - ay + dx - bz)j + (td - az + by - xc)k

    四元数偶积：Even(p,q) 

    四元数偶积也不常用，但是它也会被提到，因为它和奇积的相似性。它是纯对称的积；因此，它是完全可交换的。

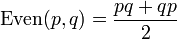
    operatorname{Even}(p,q) = frac{pq + qp}{2}

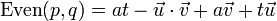
    operatorname{Even}(p,q) = at - vec{u}cdotvec{v} + avec{v} + tvec{u}

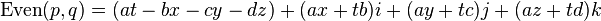
    operatorname{Even}(p,q) = (at - bx - cy - dz) + (ax + tb)i + (ay + tc)j + (az + td)k

    四元数叉积：p × q

    四元数叉积也称为奇积。它和向量叉积等价，并且只返回一个向量值：

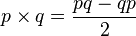
    p imes q = frac{pq - qp}{2}

    p imes q = vec{u} imesvec{v}

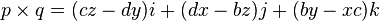
    p imes q = (cz - dy)i + (dx - bz)j + (by - xc)k

    四元数的逆：p−1

    四元数的逆通过p−1p = 1被定义。 它定义在上面的定义一节，位于属性之下（注意变量记法的差异）。其建构方式相同于复倒数(complex inverse)之构造：

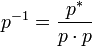
    p^{-1} = frac{p^*}{pcdot p}

    一个四元数的自身点积是个标量。四元数除以一个标量等效于乘上此标量的倒数，而使四元数的每个元素皆除以此一除数。

    四元数除法：p−1q 

    四元数的不可换性导致了 p−1q 和 qp−1的不同。 这意味着除非p是一个标量,否则不能使用q/p这一符号。

    四元数标量部：Scalar(p) 

    四元数的标量部分可以用前面所述的点积来分离出来：

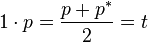
    1cdot p = frac{p + p^*}{2} = t

    四元数向量部：Vector(p) 

    四元数的向量部分可以用外积提取出来，就象用点积分离标量那样：

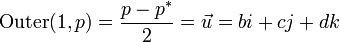
    operatorname{Outer}(1, p) = frac{p - p^*}{2} = vec{u} = bi + cj + dk

    四元数模：|p| 

    四元数的绝对值是四元数到原点的距离。

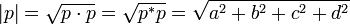
    |p| = sqrt{p cdot p} = sqrt{p^*p} = sqrt{a^2 + b^2 + c^2 + d^2}

    四元数符号数：sgn(p) 

    一复数之符号数乃得出单位圆上，一个方向与原复数相同之复数。四元数的符号数亦产生单位四元数：

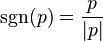
    sgn(p) = frac{p}{|p|}

    四元数辐角：arg(p) 

    辐角函数可找出一4-向量四元数偏离单位标量(即：1)之角度。此函数输出一个标量角度。

    arg(p) = arccosleft(frac{operatorname{Scalar}(p)}{|p|} ight)

     



  • 相关阅读:
    关于$.ajax同步和异步的问题和提交后台的一些问题。
    maven的web项目手工发布
    eclipse中的maven配置
    springmvc转页面
    javax.validation.ValidationException: Unable to create a Configuration, because no Bean Validation provider could be found. Add a provider like Hibernate Validator (RI) to your classpath.
    Maven项目导入后打红色X
    springmvc 拦截器，不拦截jsp文件
    RAID 磁盘阵列
    消息队列
    查看占用内存最高的进程
  • 原文地址：https://www.cnblogs.com/jins-note/p/9512660.html
Copyright © 2011-2022 走看看