知识复习
空间亚线性算法:由于大数据算法中涉及到的数据是海量的,数据难以放入内存计算,所以一种常用的处理办法是不对全部数据进行计算,而只向内存里放入小部分数据,仅使用内存中的小部分数据,就可以得到一个有质量保证的结果。
数据流算法:是指数据源源不断地到来,根据到来的数据返回相应的部分结果。适用于两种情况:第一、数据量非常大仅能扫描一次时,可以把数据看成数据流,把扫描看成数据到来。第二、数据更新非常快,不能把所有数据都保存下来再计算结果,此时可以把数据看成是一个数据流。
在一些情况下,空间亚线性算法也叫数据流算法。
水库抽样(海量数据随机抽样问题)(蓄水池问题)
输入:一组数据,其大小未知
输出:这组数据的k个均匀抽样
要求:
仅扫描数据一次。
空间复杂度为O(K)。空间复杂度与整个数据量无关,只与抽样大小有关。
扫描到数据的前n 个数据时(n>k),保存当前已扫描数据的k个均匀抽样。
问题可以理解为:蓄水池(水库)的容量为k,对于n(n>k)个元素,如果第i个元素(i从1逐渐递增至n)以k/i的概率决定是否将它放入蓄水池,当i=n时,蓄水池中存放的是n个元素的均匀抽样,每个数字最终被存在数组中的概率相等,为k/n。见下面的证明
水库抽样算法描述
1、申请一个长度为k的数组A保存抽样。
2、保存首先接收到的k个元素
3、当接收到第i个新元素t时,以k/i的概率随机替换A中的元素(即生成[1,i]间随机数j,若j<=k,则以t替换A[j])
Init : a reservoir with the size: k
for i= k+1 to N
M=random(1, i);
if( M < k)
SWAP the Mth value and ith value
end for
证明一
当接收到第i个新元素t时,以k/i的概率保存在水库中,所以在接收第i+1个数时,第i个数还能保存在水库当中的概率是1-1/(i+1),因为在接收到第i+1个数时要以k/(i+1)的概率随机替换,而第i个数被选中的概率是1/k,它们相乘即为1/(i+1)。1/(i+1)为第i个元素被换出水库的概率,所以1-1/(i+1)就是在接收第i+1个元素时第i个元素在数组中的概率。同理,在接收第i+2个元素时,第i个元素让然保留在水库中的概率为1-1/(i+2)。以此类推,当接收第n个元素时,第i个元素保存在水库中的概率为1-1/n。只有这些事件都放生了,最终第i个元素才能保留在水库当中。因此第i个元素最终被保留在水库抽样当中的概率,就是这些事件的概率的乘积,即
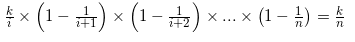
证明二
(1)第一步初始化。出现在水库中的前k个元素,直接保存在数组A中。前k个数被选中的概率都是一致的,都是1。
情况1:第k+1个元素未被选中,数组中没有元素被替换;此时,数组中每个元素的出现概率肯定是一样的,这很显然。但具体是多少呢?就是第k+1个元素未被选中的概率:1-P(第k+1个元素被选中)=1-k/(k+1)=1/(k+1)。(由于第k+1个元素被选中的概率是k/(k+1)(根据公式k/i))
情况2:第k+1个元素被选中,数组中某个元素被第k+1个元素替换掉。第k+1个元素被选中的概率是k/(k+1)(根据公式k/i),所以这个新元素在水库中出现的概率就一定是k/(k+1)(不管它替换掉哪个元素)。下面来看水库中原有元素最终还能留在水库中的概率,水库中原有数据被替换的几率都相等为1/k。水库中任意一个元素被替换掉的概率是:(k/k+1)*(1/k)=1/(k+1),意即首先要第k+1个元素被选中,然后该元素在k个元素中被选中。那它未被替换的概率就是1-1/(k+1)=k/(k+1)。可以看出来,旧元素和新元素出现的概率是相等的。
(3)第k+1之后面每个元素都重复第二步,即第i (i>k+1)个元素以k/i的概率决定是否将它放入蓄水池,最终所有元素出现在水库中的概率相等。