一、 有向图概述
和无向图不同,有向图是具有指向性的图,是由一组顶点和若干有方向的边组成,每个有方向的边都连着两个有序的顶点。向有向图添加一条边时,只会根据指向有顶点v新增一条指向w的边
不需要w->v再添加一条。
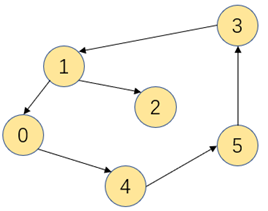

二、 有向图定义与实现
出度:某个顶点指出的边的条数为该顶点的出度
入度:指向某个顶点的边的条数为该顶点的入度
有向路径:由一组顶点和若干有方向的边组成,每个有方向的边都连着两个有序的顶点,称为有向路径。
有向环:至少含有一条边,且起点和终点相同的有向图
|
import com.data.struct.common.list.queue.Queue; /** * 有向图实现 * @author jiyukai */ public class Digraph { //定点个数 public int V;
//边的数量 public int E;
//图的邻接表 public Queue<Integer>[] qTable;
public Digraph(int v) { this.V = v;
this.E = 0;
//初始化邻接表,数组中的索引为顶点,值为已队列,存放相邻的顶点 qTable = new Queue[v]; for(int i=0;i<v;i++) { qTable[i] = new Queue<Integer>(); } }
/** * 向图中添加一条有向边 * @param v * @param w */ public void addEdge(int v,int w) { //顶点v添加w的指向 qTable[v].enqueue(w);
//边加1 E++; }
/** * 返回当前顶点的数量 * @return */ public int V() { return V; }
/** * 返回当前边的数量 * @return */ public int E() { return E; }
/** * 获取与顶点V相邻的顶点 * @param V * @return */ public Queue adjoin(int V) { return qTable[V]; }
/** * 获取该有向图的反向图 * @return */ public Digraph reverse() { Digraph digraph = new Digraph(V); for(int v=0;v<V;v++) { for(int w : digraph.qTable[v]) { //上述有向图实现为添加v-w的有向边,现在反着添加w-v的有向边即可 digraph.addEdge(w, v); } } return digraph; } } |
三、 拓扑图概述
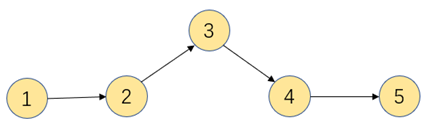
每天上下班的地铁可能涉及转车,把每个站看成一个顶点,则顶点的到达是有序,如下图,要去地铁站5,则需有序的从1转到2转到3转到4,最后再转站到5,这样也形成了一副有向图
对于一副有向图,若存在若干有序的顶点,且每条有向边都从排序靠前的顶点指向排序靠后的顶点,这样的图为经过拓扑排序后的有向图。
四、 有向环检测
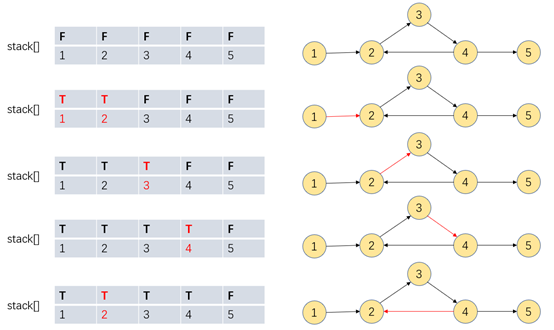
如下图,存在2-3-4-2的有向环,所以在解决拓扑图这种带有顶点优先级的问题时,需要检测图中是否存在有向环,避免陷入死循环。

在有向环的检测中,我们可以开辟一个数组,索引为顶点,值为布尔值,对于搜索过的顶点我们标记为true,未搜索过的初始化为false,当搜索到某一个顶点时,若发现它的值为true
则证明在之前已被搜索标记过,此时可以判断存在有向环
|
import com.data.struct.common.graph.Graph; /** * 检测有向图中是否有环 * @author jiyukai */ public class DirectedCycle { //标记顶点x是否有被搜索过 public boolean[] flags; public int count; //记录图中是否有环 private boolean hasCycle; /** * 深度优先搜索,找出与顶点V想通的所有顶点 * @param G * @param V */ public DirectedCycle(Graph G,int V) { //长度置0 this.count = 0;
//创建一个与顶点数量相同的标记数组,标记每个顶点是否被搜索过 flags = new boolean[G.V()];
//初始化默认无环 hasCycle = false;
//深度优先搜索,检测有环需遍历图中每一个点 for(int v=0;v<V;v++) { if(!flags[v]) { dfs(G, v); } } } /** * 深度优先搜索实现 * @param G * @param V */ public void dfs(Graph G,int V) { //被搜的顶点V标记为搜索过 flags[V] = true;
for(int w : G.qTable[V]) { if(!flags[w]) { dfs(G, w); }
if(flags[w]) { hasCycle = true; return; } }
//相通的点+1 count++; } /** * 返回与顶点V相通的所有顶点 * @return */ public int count() { return count; } /** * 判断顶点w是否与v相通 * @param w * @return */ public boolean isConnected(int w) { return flags[w]; } } |
五、 基于深度优先的顶点搜索实现拓扑排序
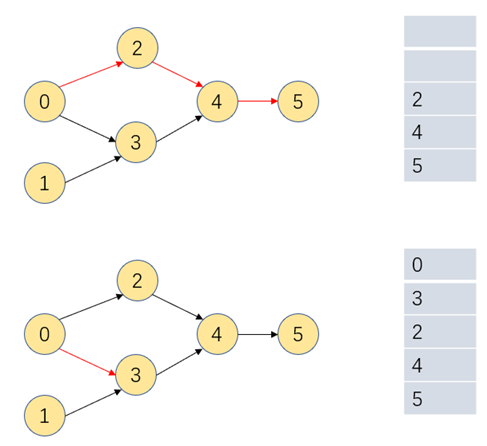
我们可以基于图的深度优先搜索来找出一副有向图中按顺序排列的顶点,开辟一个栈用于存放有序顶点的集合,从一个顶点开始递归深度搜索它的邻接顶点,搜索到不再具备递归条件
即到达最后一个顶点时,将顶点入栈,作为优先级最靠后的顶点,同时将该顶点标记为已搜索;之后依次将搜索的顶点入栈,若搜索的顶点已被标记,则不重复入栈,最后将栈中的顶点依次取出
则可以找出一副有向图中按顺序排列的顶点。
|
import com.data.struct.common.graph.Graph; import com.data.struct.common.list.stack.Stack; /** * 基于深度优先搜索的拓扑排序 * @author jiyukai */ public class DepthFirstOrder { //标记顶点x是否有被搜索过 public boolean[] flags;
public int count;
//使用栈,存储顶点序列 private Stack<Integer> stack;
/** * 深度优先搜索,找出与顶点V想通的所有顶点 * @param G * @param V */ public DepthFirstOrder(Graph G,int V) { //长度置0 this.count = 0;
//创建一个与顶点数量相同的标记数组,标记每个顶点是否被搜索过 flags = new boolean[G.V()];
//深度优先搜索,检测有环需遍历图中每一个点 for(int v=0;v<V;v++) { if(!flags[v]) { dfs(G, v); } }
}
/** * 深度优先搜索实现 * @param G * @param V */ public void dfs(Graph G,int V) { //被搜的顶点V标记为搜索过 flags[V] = true;
for(int w : G.qTable[V]) { if(!flags[w]) { dfs(G, w); } }
//顶点进栈 stack.push(V);
//相通的点+1 count++; }
/** * 返回与顶点V相通的所有顶点 * @return */ public int count() { return count; }
/** * 判断顶点w是否与v相通 * @param w * @return */ public boolean isConnected(int w) { return flags[w]; }
/** * 获取顶点的顺序栈 * @return */ public Stack<Integer> getOrderStack(){ return stack; } } |