形式语言与自动机 --- 上下文无关语言 & 下推自动机

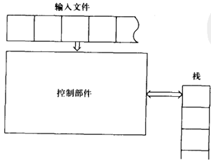
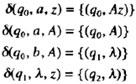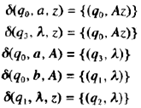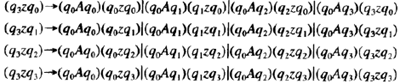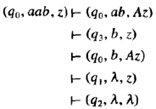一、下推自动机(pushdown automata)

下推自动机是一个带栈的自动机，用于信息暂存和比对。非确定型下推自动机由一个七元组定义：

[例]针对语言 L={w∈{a,b}*:na(w)=nb(w)}构造一个npda。

     

在处理baab过程中，该npda执行的迁移如下：

二、下推自动机与上下文无关语言

(a)证明：对于任何的上下文无关语言L，存在一个npda M使得L=L(M)。

npda可表示为：

其转移函数包括：

，

目标是证明：若，则：

假设文法化为格里巴范式，根据定义和上式得：

设w=a1a2…an，则：

，根据规则得：

则存在使得：

如此重复，设得到：

这使得任一时刻栈的内容（z除外）与句型中没有匹配的部分是一致的，因此：

若语言不包含空，则；若包含空，则加入，证毕。

(b)证明对于任何的npda，存在一个上下文无关文法与之对应。

简化问题，假定npda满足：

1.只有一个终态qf，且栈为空时进入终态。

2.所有转移函数形如：，其中或，也就是说每次迁移对栈进行的修改要么增加一个符号，要么减少一个符号。

为构造一个文法满足上述条件，则存在产生式和（为了擦除A，当读到a并且从qi到qj转换时，首先用BC替换A，接下来状态从qj转换到ql并擦除B，然后从ql转换到qk并擦除C）。

以作为开始符，则，当读入w从q0转换到qf时，npda删除z（创建空栈），这就是npda接受w的过程。因此由文法生成的语言与npda接受的语言相同。证毕

[例]考虑npda，转移函数如下：

   

q0为初态，q2为终态，该npda满足1但不满足2，为满足2引入新状态q3和中间步骤，在该步骤中线从栈中删除A，然后在下一次迁移中替换它。新规则集合为：

  

后三个转移函数得到相应产生式：

根据前两个转移函数得到产生式集合，其中开始变量为：：

符号串aab通过如下连续迁移能被pda接受：

三、确定型下推自动机和确定型上下文无关语言（每一步迁移都是唯一的）

若下推自动机是确定型的，则还满足限制条件：

1.对任意给定的输入符号与栈顶符号，最多只能进行一种迁移；

2.若一格局存在空迁移，则不能有读入输入符号的迁移。如：和。

四、两个泵引理

1.上下文无关语言的泵引理

设L是一个无穷上下文无关语言，则存在一个|w|≥m的w(w∈L)能分解为：w=uvxyz。

其中：|vxy|≤m 且 |vy|≥1，对所有的i=0,1,2…满足：uvⁱxyⁱz∈L。

如下图的推导树为：

对应的推导为：

其中u,v,x,y,z都是终结符号，从上可知，因而所有的符号串,i=0,1,2…都能够根据文法声称，因此它们也属于L。

2.线性语言的泵引理（线性语言：满足线性上下文无关文法的语言）

设L是一个无穷线性语言，存在某个正整数m，使得任意w∈L（|w|≥m）都能够分解为w=uvxyz。

其中：|uvyz|≤m 且 |xy|≥1，对所有的i=0,1,2…满足：uvⁱxyⁱz∈L。

上述泵引理与1存在区别，由于2中|uvyz|≤m替换了1中的|vxy|≤m，表明可以抽取的符号串v与y必须分别位于w距左右两端长度为m的符号串中，而中间符号串x可以为任意长度。