牛客练习赛60

A 大吉大利

思路： 我们把所有数的每一位求总和，对于第一个求和符下的计算就是当(a_i)的第j位是1时，答案就加上一次第j位的总和。复杂度O(nlogn)

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N=1e5+10;
LL a[N];
long long bt[40],Pow[40];
int main(){
    int n;
    Pow[0]=1;
    for(int i=1;i<40;++i){
        Pow[i]=Pow[i-1]*2;
    }
    cin>>n;
    for(int i=1;i<=n;++i){
        cin>>a[i];
    }
    for(int i=1;i<=n;++i){
        int t=a[i];
        for(int i=0;i<40;++i){
            if(t%2) bt[i]++;
            t/=2;
        }
    }
    LL ans=0;
    for(int i=1;i<=n;++i){
        int t=a[i];
        for(int i=0;i<40;++i){
            if(t%2){
                ans+=Pow[i]*bt[i];
            }t/=2;
        }
    }
    printf("%lld
",ans);
    return 0;
}

B 三角形周长和

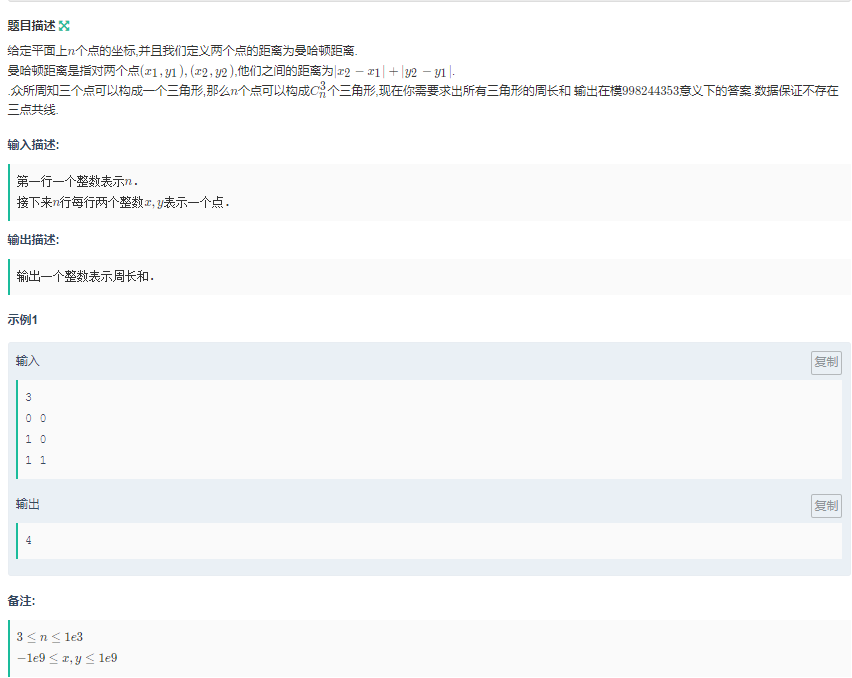
思路： 枚举每一条边，一条边在n-2个三角形里的贡献。

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int mod=998244353;
LL x[2010],y[2010];
LL dis(int i,int j){
    return (abs(x[i]-x[j])%mod+abs(y[i]-y[j])%mod)%mod;
}
int main(){
    int n;
    while(scanf("%d",&n)!=EOF){
        long long ans=0;
        for(int i=1;i<=n;++i)
            scanf("%lld%lld",&x[i],&y[i]);
        for(int i=1;i<=n;++i){
            for(int j=i+1;j<=n;++j){
                ans=(ans+dis(i,j)%mod*(n-2)+mod)%mod;
            }
        }
        cout<<ans<<endl;
    }
    return 0;
}

C 操作集锦

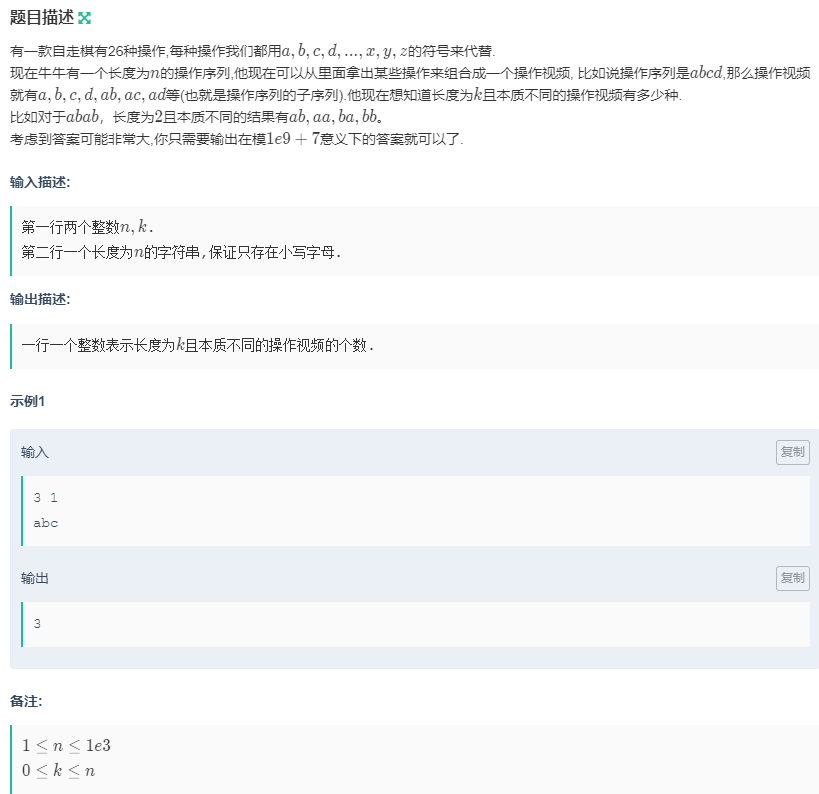
思路： 这道题是对求字符串本质不同的子序列个数问题的扩展。
子序列个数
对于f[i]表示前i个字符可以组成的本质不同的子序列，如果a[i]表示的字符是第一次出现 f[i]=f[i-1]+f[i-1]+1，表示它加在和f[i-1]个不同子序列后面组成新的串以及单独成一个；如果a[i]不是第一次出现，上一次出现的位置在last[a[i]]，则f[i]=f[i-1]+f[i-1]-f[last[i-1]]，表示它可以加在f[i-1]个不同子序列后面组成新的串但是last[a[i]-1]之前的子序列已经和last[a[i]]组成一次了。

#include<iostream>
#include<string.h>
#include<cstdio>
#include<cmath>
#include<algorithm>
#include<queue>
#include<vector>
#include<string>
#include<set>
#include<map>
using namespace std;
typedef pair<int,int> PII;
typedef long long LL;
const int N=1000010,mod=1e9+7;
int s[N];
LL f[N],last[N];
int main(){
    int n;
    while(scanf("%d",&n)!=EOF){
        for(int i=1;i<=n;++i) scanf("%d",&s[i]);
        LL res=0;
        memset(last,-1,sizeof last);
        for(int i=1;i<=n;++i){
            int c=s[i];
            if(last[c]==-1)
                f[i]=f[i-1]*2+1;
            else f[i]=f[i-1]+f[i-1]-f[last[c]-1]+mod;
            f[i]%=mod;
            last[c]=i;
        }
        printf("%lld
",f[n]);
    }
    return 0;
}

对于这道题需要多记录一个状态，f[i,j]表示前i个字符可以组成的长度为j的子序列个数

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int mod=1e9+7;
const int N=1e3+10;
long long f[N][N],last[30];
char str[N];
int main(){
    int n,k;
    cin>>n>>k;
    cin>>str+1;
    memset(last,-1,sizeof last);
    f[0][0]=1;
    for(int i=1;i<=n;++i){
        int c=str[i]-'a';
        f[i][0]=1;
        for(int j=1;j<=k&&j<=i;++j){
            if(last[c]==-1)
                f[i][j]=(f[i-1][j]+f[i-1][j-1])%mod;
            else
                f[i][j]=(f[i-1][j]+f[i-1][j-1]-f[last[c]-1][j-1]+mod)%mod;
        }
        last[c]=i;
    }
    cout<<f[n][k]<<endl;
    return 0;
}

斩杀线计算大师

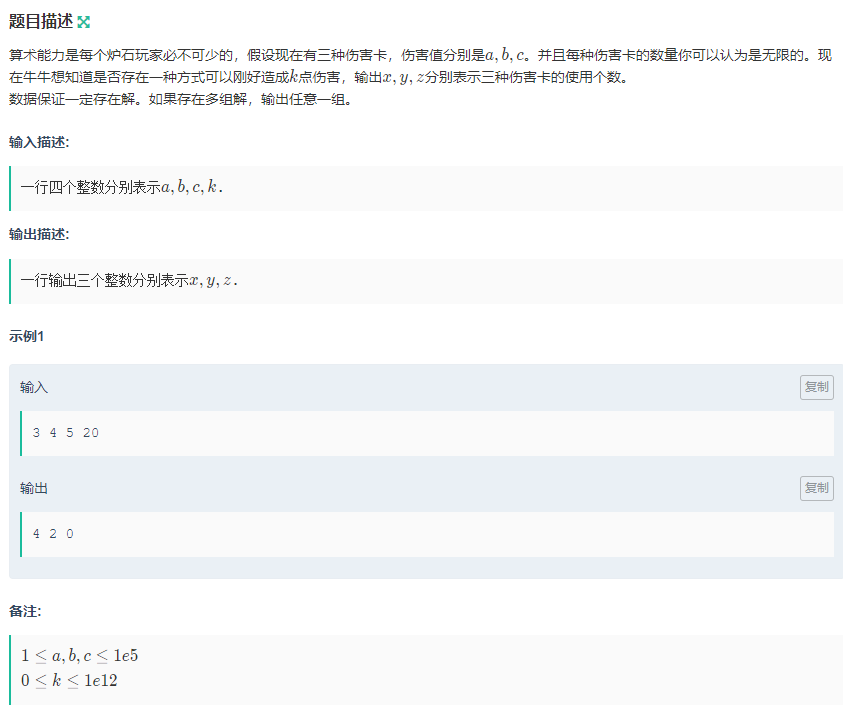
思路： 要解 (a*x+b*y+c*z=k)，转化为 (t*gcd(a,b)+c*z=k) exgcd解出t,z，再转化为 (a*x+b*y=k-z*c) ，虽然本题一定有解，但我们解2个方程，情况有2*2种，所有我们需要去枚举第一个方程的cz，计算三次，输出任意一次有解的可能。

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
LL gcd(LL a,LL b){
    return b==0 ? a : gcd(b,a%b);
}
LL exGcd(LL &x,LL &y,LL a,LL b){
    if(b==0){
        x=1,y=0;
        return a;
    }
    LL GCD=exGcd(x,y,b,a%b);
    LL t=x;
    x=y;
    y=t-a/b*y;
    return GCD;
}
bool solve(LL a,LL b,LL c,LL k,int Case){
    LL gab=gcd(a,b);
    LL t,x,y,z;
    exGcd(t,z,gab,c);//gab*t+c*z=1
    LL gabc=gcd(gab,c);
    t*=(k/gabc);
    z*=(k/gabc);
    if(z<0) {
        LL tmp=(-z)/(gab/gabc);
        z+=gab/gabc*tmp;
        t-=c/gabc*tmp;
        if(z<0) z+=gab/gabc,t-=c/gabc;
    }
    if(t<0){
        LL tmp=(-t)/(c/gabc);
         z-=gab/gabc*tmp;
        t+=c/gabc*tmp;
        if(t<0) z-=gab/gabc,t+=c/gabc;
    }
    k-=z*c;
    exGcd(x,y,a,b);
    x*=(k/gab),y*=(k/gab);
    if(x<0){
        LL tmp=(-x)/(b/gab);
        x+=tmp*(b/gab);
        y-=a/gab*tmp;
        if(x<0) x+=(b/gab),y-=a/gab;
    }
    if(y<0){
        LL tmp=(-y)/(a/gab);
        x-=tmp*(b/gab);
        y+=a/gab*tmp;
        if(y<0) x-=(b/gab),y+=a/gab;
    }
    if(x>=0&&y>=0&&z>=0){
        if(Case==1)
            cout<<x<<" "<<y<<" "<<z<<endl;
        else if(Case==2)
            cout<<z<<" "<<y<<" "<<x<<endl;
        else cout<<x<<" "<<z<<" "<<y<<endl;
        return true;
    }
    else return false;
}
int main(){
    LL a,b,c,k;
    cin>>a>>b>>c>>k;
    if(solve(a,b,c,k,1)) return 0;
    if(solve(c,b,a,k,2)) return 0;
    if(solve(a,c,b,k,3)) return 0;
    return 0;
}
//234 2234 324 241520