卡特兰数 Catalan number

公式：

卡特兰数的一种常用计算公式：C(2n,n)-C(2n,n-1)

证明：

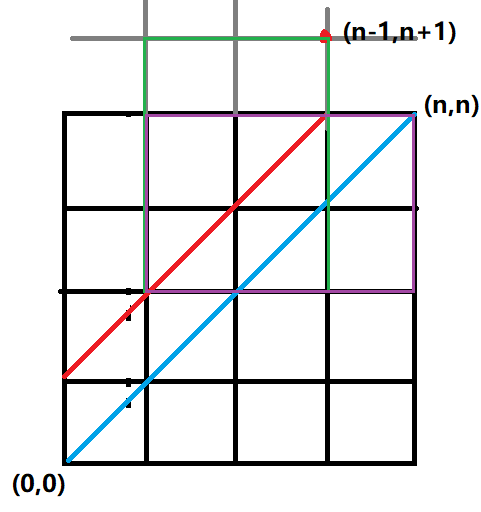
从(0,0)出发到(n,n)，每次只能向右或向上，不可以越过蓝线，即不能走到红线上。如果不受红线限制从(0,0)出发到(n,n)的所有方案有C(2n,n)中，可以理解为在2n次移动中选择n次做向右或向上运动。那么拿全集减去走到红线上的方案就是要求的合法方案了。

假设一定走到红线上，我们关于红线作(0,0)的轴对称，就是(n-1,n+1),所有在红线点上到(n-1,n+1)的路线都与到红线点上再走到(n,n)关于红线对称。那么从(0,0)出发到(n-1,n+1)的所有方案就一定经过红线，看绿色框和紫色框。所以经过红线的方案数就是C(2n,n-1)。