前面我们讲解了并不像数组一样完全作为存储数据功能,而是作为构思算法的辅助工具的数据结构——栈,本文我们介绍另外一个这样的工具——队列。栈是后进先出,而队列刚好相反,是先进先出。
1、队列的基本概念
队列(queue)是一种特殊的线性表,特殊之处在于它只允许在表的前端(front)进行删除操作,而在表的后端(rear)进行插入操作,和栈一样,队列是一种操作受限制的线性表。进行插入操作的端称为队尾,进行删除操作的端称为队头。队列中没有元素时,称为空队列。
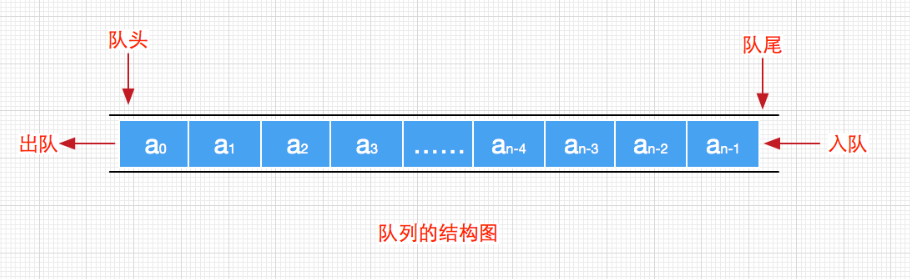
队列的数据元素又称为队列元素。在队列中插入一个队列元素称为入队,从队列中删除一个队列元素称为出队。因为队列只允许在一端插入,在另一端删除,所以只有最早进入队列的元素才能最先从队列中删除,故队列又称为先进先出(FIFO—first in first out)线性表。
比如我们去电影院排队买票,第一个进入排队序列的都是第一个买到票离开队列的人,而最后进入排队序列排队的都是最后买到票的。
在比如在计算机操作系统中,有各种队列在安静的工作着,比如打印机在打印列队中等待打印。
队列分为:
①、单向队列(Queue):只能在一端插入数据,另一端删除数据。
②、双向队列(Deque):每一端都可以进行插入数据和删除数据操作。
这里我们还会介绍一种队列——优先级队列,优先级队列是比栈和队列更专用的数据结构,在优先级队列中,数据项按照关键字进行排序,关键字最小(或者最大)的数据项往往在队列的最前面,而数据项在插入的时候都会插入到合适的位置以确保队列的有序。
2、Java模拟单向队列实现
在实现之前,我们先看下面几个问题:
①、与栈不同的是,队列中的数据不总是从数组的0下标开始的,移除一些队头front的数据后,队头指针会指向一个较高的下标位置,如下图:

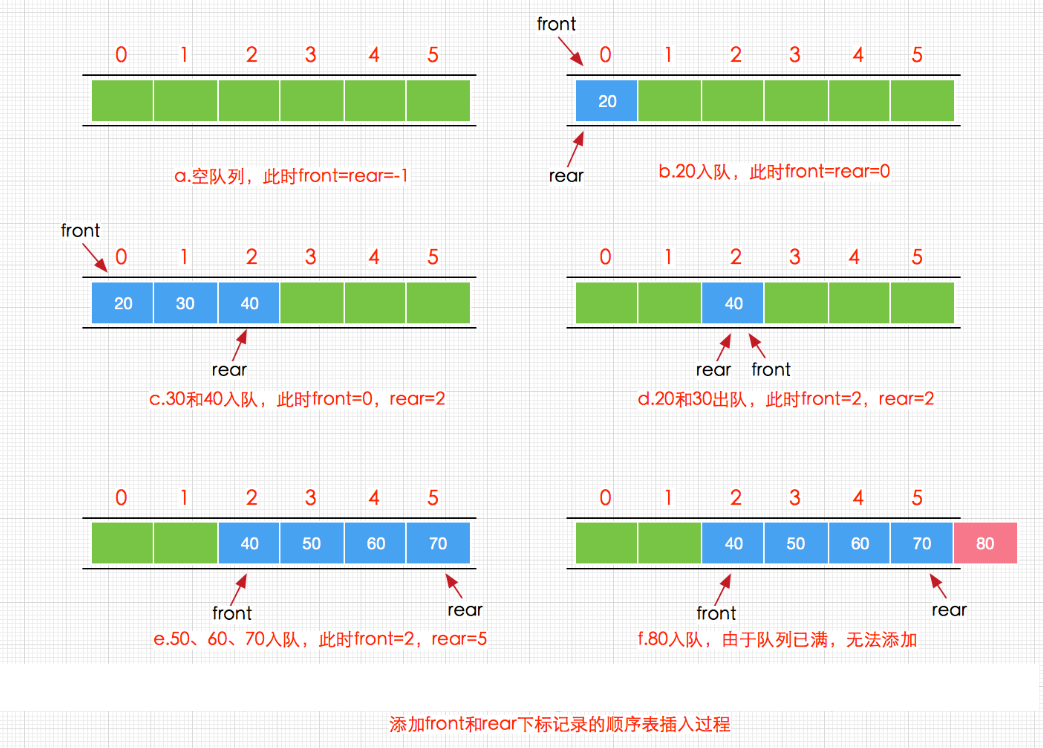
图1 图2
②、我们再设计时,如图1,队列中新增一个数据时,队尾的指针rear 会向上移动,也就是向下标大的方向。移除数据项时,队头指针 front 也会向下移动。那么这样设计好像和现实情况相反,比如排队买电影票,队头的买完票就离开了,然后队伍整体向前移动。在计算机中也可以在队列中删除一个数之后,队列整体向前移动,但是这样做效率很差。我们选择的做法是移动队头和队尾的指针。
从图2的演示过程中,我们可以看出,(a)操作时,是空队列此时front和rear都为-1,同时可以发现虽然我们通过给顺序表添加front和rear变量记录下标后使用得出队操作的时间复杂度降为O(1),但是却出现了另外一个严重的问题,那就是空间浪费,从图中的(d)和(e)操作可以发现,20和30出队后,遗留下来的空间并没有被重新利用,反而是空着,所以导致执行(f)操作时,出现队列已满的假现象,这种假现象我们称之为假溢出,之所以出现这样假溢出的现象是因为顺序表队列的存储单元没有重复利用机制,而解决该问题的最合适的方式就是将顺序队列设计为循环结构,接下来我们就通过循环顺序表来实现顺序队列。
③、如果向第②步这样移动指针,相信队尾指针很快就移动到数据的最末端了,这时候可能移除过数据,那么队头会有空着的位置,然后新来了一个数据项,由于队尾不能再向上移动了,那该怎么办呢?如下图:

为了避免队列不满却不能插入新的数据,我们可以让队尾指针绕回到数组开始的位置,这也称为“循环队列”。

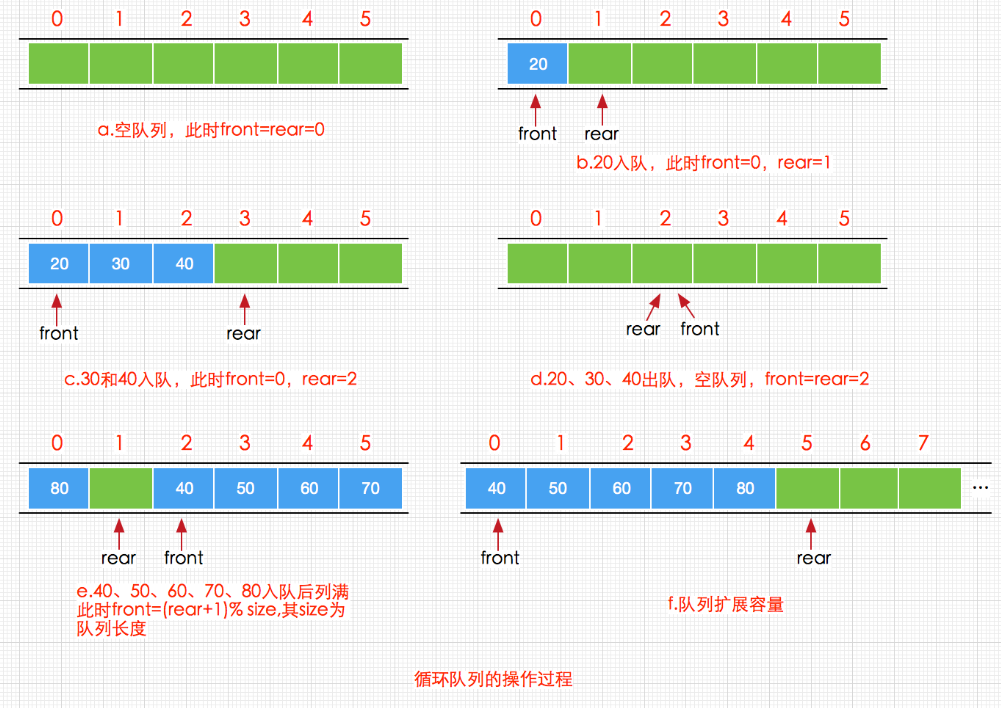
弄懂原理之后,Java实现代码如下:
public class MyQueue { private Object[] queArray; // 队列总大小 private int maxSize; // 前端 private int front; // 后端 private int rear; // 队列中元素的实际数目 private int nItems; public MyQueue(int s) { maxSize = s; queArray = new Object[maxSize]; front = 0; rear = -1; nItems = 0; } // 队列中新增数据 public void insert(int value) { if (isFull()) { System.out.println("队列已满!!!"); } else { // 如果队列尾部指向顶了,那么循环回来,执行队列的第一个元素 if (rear == maxSize - 1) { rear = -1; } // 队尾指针加1,然后在队尾指针处插入新的数据 queArray[++rear] = value; nItems++; } } // 移除数据 public Object remove() { Object removeValue = null; if (!isEmpty()) { removeValue = queArray[front]; queArray[front] = null; front++; if (front == maxSize) { front = 0; } nItems--; return removeValue; } return removeValue; } // 查看对头数据 public Object peekFront() { return queArray[front]; } // 判断队列是否满了 public boolean isFull() { return (nItems == maxSize); } // 判断队列是否为空 public boolean isEmpty() { return (nItems == 0); } // 返回队列的大小 public int getSize() { return nItems; } }
public class Test { public static void main(String[] args) { MyQueue queue = new MyQueue(3); queue.insert(1); queue.insert(2); queue.insert(3);//queArray数组数据为[1,2,3] System.out.println(queue.peekFront()); //1 queue.remove();//queArray数组数据为[null,2,3] System.out.println(queue.peekFront()); //2 queue.insert(4);//queArray数组数据为[4,2,3] queue.insert(5);//队列已满,queArray数组数据为[4,2,3] } }
测试结果:
1
2
队列已满!!!
3、双端队列
双端队列就是一个两端都是结尾或者开头的队列, 队列的每一端都可以进行插入数据项和移除数据项,这些方法可以叫做:
insertRight()、insertLeft()、removeLeft()、removeRight()
如果严格禁止调用insertLeft()和removeLeft()(或禁用右端操作),那么双端队列的功能就和前面讲的栈功能一样。
如果严格禁止调用insertLeft()和removeRight(或相反的另一对方法),那么双端队列的功能就和单向队列一样了。
4、优先级队列
优先级队列(priority queue)是比栈和队列更专用的数据结构,在优先级队列中,数据项按照关键字进行排序,关键字最小(或者最大)的数据项往往在队列的最前面,而数据项在插入的时候都会插入到合适的位置以确保队列的有序。
优先级队列 是0个或多个元素的集合,每个元素都有一个优先权,对优先级队列执行的操作有:
(1)查找
(2)插入一个新元素
(3)删除
一般情况下,查找操作用来搜索优先权最大的元素,删除操作用来删除该元素 。对于优先权相同的元素,可按先进先出次序处理或按任意优先权进行。
这里我们用数组实现优先级队列,这种方法插入比较慢,但是它比较简单,适用于数据量比较小并且不是特别注重插入速度的情况。
后面我们会讲解堆,用堆的数据结构来实现优先级队列,可以相当快的插入数据。
数组实现优先级队列,声明为int类型的数组,关键字是数组里面的元素,在插入的时候按照从大到小的顺序排列,也就是越小的元素优先级越高。
public class PriorityQue { private int maxSize; private int[] priQueArray; private int nItems; public PriorityQue(int s) { maxSize = s; priQueArray = new int[maxSize]; nItems = 0; } // 插入数据 public void insert(int value) { int j; if (nItems == 0) { priQueArray[nItems++] = value; } else { j = nItems - 1; // 选择的排序方法是插入排序,按照从大到小的顺序排列,越小的越在队列的顶端 while (j >= 0 && value > priQueArray[j]) { priQueArray[j + 1] = priQueArray[j]; j--; } priQueArray[j + 1] = value; nItems++; } } // 移除数据,由于是按照大小排序的,所以移除数据我们指针向下移动 // 被移除的地方由于是int类型的,不能设置为null,这里的做法是设置为 -1 public int remove() { int k = nItems - 1; int value = priQueArray[k]; priQueArray[k] = -1;// -1表示这个位置的数据被移除了 nItems--; return value; } // 查看优先级最高的元素 public int peekMin() { return priQueArray[nItems - 1]; } // 判断是否为空 public boolean isEmpty() { return (nItems == 0); } // 判断是否满了 public boolean isFull() { return (nItems == maxSize); } }
insert() 方法,先检查队列中是否有数据项,如果没有,则直接插入到下标为0的单元里,否则,从数组顶部开始比较,找到比插入值小的位置进行插入,并把 nItems 加1.
remove 方法直接获取顶部元素。
优先级队列的插入操作需要 O(N)的时间,而删除操作则需要O(1) 的时间,后面会讲解如何通过 堆 来改进插入时间。
5、总结
本篇博客我们介绍了队列的三种形式,分别是单向队列、双向队列以及优先级队列。其实大家听名字也可以听得出来他们之间的区别,单向队列遵循先进先出的原则,而且一端只能插入,另一端只能删除。双向队列则两端都可插入和删除,如果限制双向队列的某一段的方法,则可以达到和单向队列同样的功能。最后优先级队列,则是在插入元素的时候进行了优先级别排序,在实际应用中单项队列和优先级队列使用的比较多。后面讲解了堆这种数据结构,我们会用堆来实现优先级队列,改善优先级队列插入元素的时间。
通过前面讲的栈以及本篇讲的队列这两种数据结构,我们稍微总结一下:
①、栈、队列(单向队列)、优先级队列通常是用来简化某些程序操作的数据结构,而不是主要作为存储数据的。
②、在这些数据结构中,只有一个数据项可以被访问。
③、栈允许在栈顶压入(插入)数据,在栈顶弹出(移除)数据,但是只能访问最后一个插入的数据项,也就是栈顶元素。
④、队列(单向队列)只能在队尾插入数据,对头删除数据,并且只能访问对头的数据。而且队列还可以实现循环队列,它基于数组,数组下标可以从数组末端绕回到数组的开始位置。
⑤、优先级队列是有序的插入数据,并且只能访问当前元素中优先级别最大(或最小)的元素。
⑥、这些数据结构都能由数组实现,但是可以用别的机制(后面讲的链表、堆等数据结构)实现。