SDUT 3340 数据结构实验之二叉树一：树的同构

 

数据结构实验之二叉树一：树的同构

Time Limit: 1000 ms Memory Limit: 65536 KiB

Problem Description

给定两棵树T1和T2。如果T1可以通过若干次左右孩子互换就变成T2，则我们称两棵树是“同构”的。例如图1给出的两棵树就是同构的，因为我们把其中一棵树的结点A、B、G的左右孩子互换后，就得到另外一棵树。而图2就不是同构的。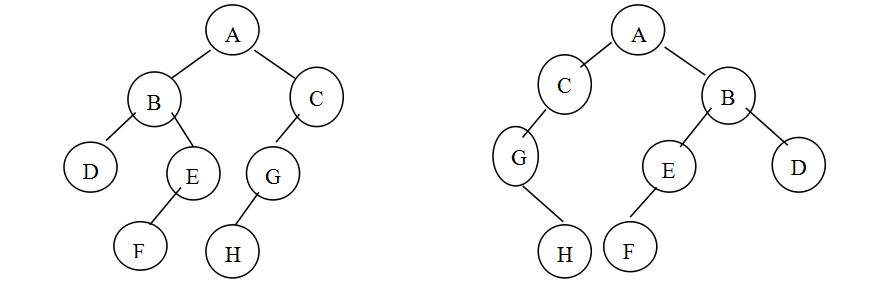

　　　　　　　　　　　　　　　　　　　　　　图1

 

　　　　　　　　　　　　　　　　　　　　　　图2

现给定两棵树，请你判断它们是否是同构的。

Input

 输入数据包含多组，每组数据给出2棵二叉树的信息。对于每棵树，首先在一行中给出一个非负整数N (≤10)，即该树的结点数（此时假设结点从0到N−1编号）；随后N行，第i行对应编号第i个结点，给出该结点中存储的1个英文大写字母、其左孩子结点的编号、右孩子结点的编号。如果孩子结点为空，则在相应位置上给出”-”。给出的数据间用一个空格分隔。
注意：题目保证每个结点中存储的字母是不同的。

Output

 如果两棵树是同构的，输出“Yes”，否则输出“No”。

Sample Input

8
A 1 2
B 3 4
C 5 -
D - -
E 6 -
G 7 -
F - -
H - -
8
G - 4
B 7 6
F - -
A 5 1
H - -
C 0 -
D - -
E 2 -

Sample Output

Yes

提示：本题可以通过建立两棵二叉树并将其遍历判断两棵二叉树是否同构.

代码实现如下（g++）：

#include <bits/stdc++.h>

using namespace std;

int n1,n2;

struct node
{
    char key;
    int left,right;
}Tree1[11],Tree2[11];

void build_tree(struct node *tree,int n)
{
    int i;
    char s[2];
    for(i=0;i<n;i++)
    {
        scanf("%s",s);
        tree[i].key=s[0];
        scanf("%s",s);
        if(s[0]=='-') tree[i].left=11;//如果是判断到“-”，则将它的数组序号变为11，即可将其删除
        else tree[i].left=s[0]-'0';
        scanf("%s",s);
        if(s[i]=='-') tree[i].right=11;//同上
        else tree[i].right=s[0]-'0';
    }
}

int judge(int i,int j)//判断两棵树是否是同构的，代码可能有点长，但是很清晰
{
    if(Tree1[Tree1[i].left].key==Tree2[Tree2[j].left].key&&Tree1[Tree1[i].right].key==Tree2[Tree2[j].right].key)return 1;
    if(Tree1[Tree1[i].left].key==Tree2[Tree2[j].right].key&&Tree1[Tree1[i].right].key==Tree2[Tree2[j].left].key)return 1;
    return 0;
}

int check()
{
    int i,j;
    for(i=0;i<n1;++i)
    {
        for(j=0;j<n2;++j)
        {
            if(Tree1[i].key==Tree2[j].key)//判断两棵树中的元素是否都相等
            {
                if(judge(i,j))break;
                else return 0;
            }
        }
        if(j==n2)return 0;
    }
    return 1;
}

int main()
{
    while(~scanf("%d",&n1))
    {
       build_tree(Tree1,n1);
       scanf("%d",&n2);
       build_tree(Tree2,n2);
       if(n2!=n1)puts("No");//如果n1、n2不相等，肯定不同构
       else if(check())puts("Yes");
       else puts("No");
    }
    return 0;
}


/***************************************************
Result: Accepted
Take time: 0ms
Take Memory: 200KB
****************************************************/