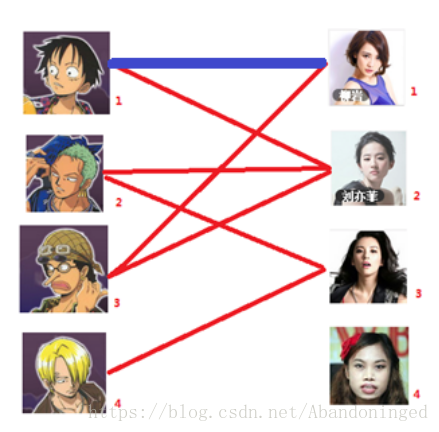
二分图，首先第一点什么是二分图：
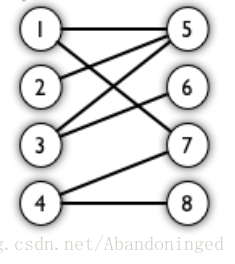
把一个图的顶点划分为两个不相交集 U 和V ，使得每一条边都分别连接U、V中的顶点。如果存在这样的划分，则此图为一个二分图。比方说下图就是一个二分图。
那么首先第一点我们要判读一个图是否为二分图，可以采用染色的思想。对于相邻的节点然不同的颜色，然后递归在这棵树上找。我们可以申明一个color数组，int color[maxn]，0代表白色，1代表黑色。对于相邻的染不同的颜色，也就是color[i]=(!color[from]);那么按照我们的定义二分图点集内不能有连线，那么如果出现起点和终点的颜色相同，那么就说明这个点集内有某条连线，也就是if(ma[from][i]&&color[from]==color[i]) return 0;
第二点就是两个重要的概念：
1.交替路：从一个未匹配点出发，依次经过非匹配边、匹配边、非匹配边…形成的路径叫交替路。
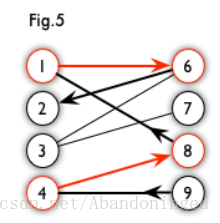
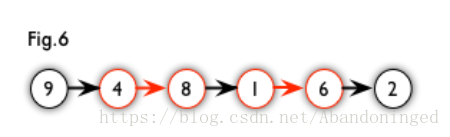
2.增广路：从一个未匹配点出发，走交替路，如果途径另一个未匹配点，则这条交替路称为增广路。例如，图 5 中的一条增广路如图 6 所示（图中的匹配点均用红色标出）：
增广路的性质：
1.长度len是奇数
2.路径上第1，3，5，……，len条边是非匹配边，第2，4，6，……，len-1条边是匹配边。
3.二分图的一组匹配 S 是最大匹配，当且仅当图中不存在增广路。
二分图的最大匹配
也就是使得所含匹配边数最多的匹配。
通过数代人的努力，终于赶上了剩男剩女的大潮，假设有N个剩男，M个剩女，每个人都可能对多名异性有好感，如果一对男女互有好感，那么你就可以把这一对撮合在一起，，你拥有的大概就是下面这样一张关系图，每一条连线都表示互有好感。
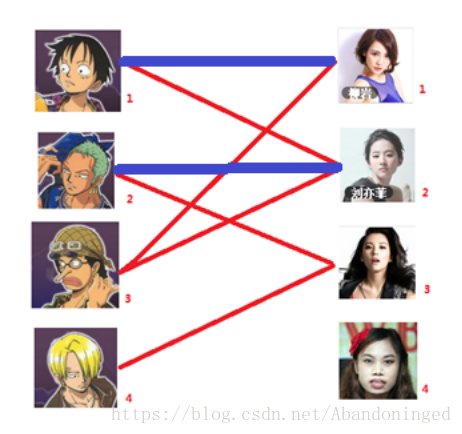
一： 先试着给1号男生找妹子，发现第一个和他相连的1号女生还名花无主，got it，连上一条蓝线
二：接着给2号男生找妹子，发现第一个和他相连的2号女生名花无主，got it
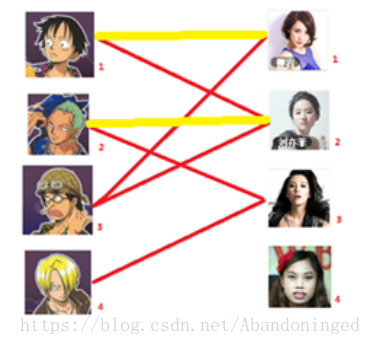
三：接下来是3号男生，很遗憾1号女生已经有主了，怎么办呢？ 我们试着给之前1号女生匹配的男生（也就是1号男生）另外分配一个妹子。 (黄色表示这条 边被临时拆掉)
与1号男生相连的第二个女生是2号女生，但是2号女生也有主了，怎么办呢？我们再试着给2号女生的原配()重新找个妹子(注意这个步骤和上面是一样的，这是一个递归的过程)
此时发现2号男生还能找到3号女生，那么之前的问题迎刃而解了，回溯回去 2号男生可以找3号妹子，1号男生可以找2号妹子了，3号男生可以找1号妹子
所以第三步最后的结果就是：
四： 接下来是4号男生，很遗憾，按照第三步的节奏我们没法给4号男生腾出来一个妹子，我们实在是无能为力了……
差不多就是这个很经典的动态图来帮忙理解这个算法，下面上模板代码：
#include <iostream>
#include <stdio.h>
#include <string>
#include <string.h>
#include <algorithm>
#include <math.h>
#include <queue>
#include <vector>
using namespace std;
typedef long long LL;
const int INF=0x3f3f3f3f;
const int maxn=105;
const double eps=1e-8;
const double pi=acos(-1.0);
const int MOD=10056;
int T,n,m,k,i;
int x,y;
int ma[maxn][maxn];//ma[i][j]=1表示xi和yj可以匹配
int vis[maxn];
int matchx[maxn],matchy[maxn];//matchx[i]表示在求得的最大匹配中与xi匹配的y顶点，matchy[i]同理
int dfs(int u)
{
for(int i=1;i<=m;i++)
{
if(ma[u][i]&&!vis[i])//找到一条没有匹配的边
{
vis[i]=1;
if((matchy[i]==-1)||dfs(matchy[i]))//若找到一条两端都没有匹配的边则已找到。注意前面的条件满足时将不会进行递归
{
matchx[u]=i;//更新匹配，原匹配已被覆盖
matchy[i]=u;
return 1;
}
}
}
return 0;
}
int cal()
{
int ans=0;
memset(matchy,-1,sizeof(matchy));
memset(matchx,-1,sizeof(matchx));
for(int i=1;i<=n;i++)
{
if(matchx[i]==-1)//每次找x中没有被覆盖的点
{
memset(vis,0,sizeof(vis));
ans+=dfs(i);
}
}
return ans;
}
int main()
{
while(scanf("%d",&n)!=EOF)
{
memset(ma,0,sizeof(ma));
if(n==0)
break;
else
scanf("%d %d",&m,&k);
while(k--)
{
scanf("%d %d %d",&i,&x,&y);
ma[x][y]=1;
}
printf("%d
",cal());
}
return 0;
}
这是无权的情况下，只要匹配的边数最大即可，那么要是有权边呢。当然它是有前提的：二分图存在完备匹配
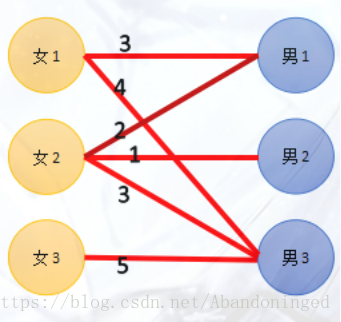
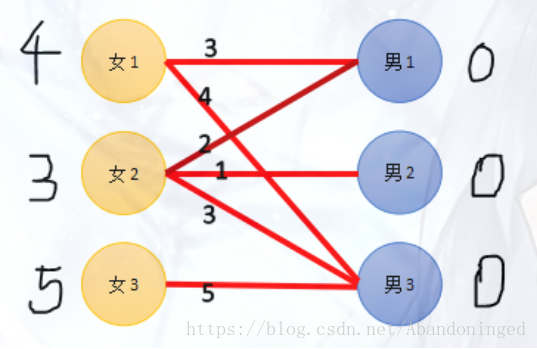
现在有N男N女，男生和女生每两个人之间有好感度，我们希望把他们两两配对，并且最后希望好感度和最大。
怎么选择最优的配对方法呢？ 首先，每个妹子会有一个期望值，就是与她有好感度的男生中最大的好感度。男生期望值为0。 这样，我们把每个人的期望值标出来。
然后，开始配对。配对方法：男女两人的期望和要等于两人之间的好感度。每一轮匹配，无论是否成功，每个男生只会被尝试匹配一次！
匹配过程：
第一轮匹配： ============================
女1：选择了男3（此时女1--男3） 女2：也想选择男3，男3已经在该轮匹配过了，女2无其他合适选择，匹配失败。 ===============================
这一轮参与匹配的人有：女1，女2，男3。 怎么办？很容易想到的，这两个女生只能降低一下期望值了，降低多少呢？两个妹子都在能选择的其他人中，也就是没参与这轮匹配的男生中，选择一个期望值降低的尽可能小的人。也就是在其他人中选择一个最合适的。 比如：女1选择男1，期望值要降低1。 女2选择男1，期望值要降低1。 女2选择男2，期望值要降低2。 于是，只要期望值降低1，就有妹子可能选择其他人。所以妹子们的期望值要降低1点。 同时，刚才被抢的男生此时非常得意，因为有妹子来抢他，与是他的期望值提高了1点（就是同妹子们降低的期望值相同）。 于是期望值变成这样（当然，不参与刚才匹配过程的人期望值不变）
第二轮匹配： ============================
（女1已经在第一轮匹配完成了，女1--男3） 女2：选择男1。（此时女1--男3，女2--男1） 女3：选择男3，男3已经有女1了，于是女1尝试换人，换到男1，男1已经被在这一轮被尝试匹配过了。于是女1换人失败，这一轮匹配失败。 ============================
再一次改变期望值。 这次三个女生都参与了匹配，男1和男3参与匹配。女生尝试换人，于是期望值降低1。参与匹配的男生期望值增加1。
第三轮匹配： ============================
上一轮女1和女2是匹配完成的。（此时女1--男3，女2--男1） 女3：选择男3，男3的当前对象女1尝试换人，换到了男1，但是男1已经有女2了，于是女2再尝试换人，换到了男2，于是女2--男2，女1--男1，女3--男3 匹配成功！！！撒花~~ ============================
虽然不停换人的过程听起来很麻烦，但其实整个是个递归的过程，实现起来比较简单。比较复杂的部分就是期望值的改变，但是可以在递归匹配的过程中顺带求出来（这样的复杂度是O（n^3））
觉得不好理解可以看模板代码：
二分图经常解决的问题：
最大匹配数：最大匹配的匹配边的数目
求法：直接上模板求
最小点覆盖数：选取最少的点，使任意一条边至少有一个端点被选择
求法：最大匹配边数 = 最小点覆盖数 证明要点： 最大匹配是原二分图边集的一个子集，并且所有边都不相交，所以至少要从每条匹配边中选出一个端点，所以 最小点覆盖数>=最大匹配边数。 对任意二分图可以构造出一组点覆盖，其包含的点数等于最大匹配包含的边数。
最大独立数：选取最多的点，使任意所选两点均不相连
求法：最大独立数 = 顶点数 - 最大匹配数 proof： 选出最多的点构成独立集 <=>在图中去掉最少的点，使剩下的点之间没有边 <=>用最少的点覆盖所有的边 因此，去掉二分图的最小点覆盖，剩余的点就构成二分图的最大独立集，而最小点覆盖等于最大匹配数。得证。
最小路径覆盖数：对于一个 DAG（有向无环图），选取最少条简单路径，使得每个顶点属于且仅属于一条路径。路径长可以为 0（即单个点）
求法：最小路径覆盖数 = 顶点数 - 原DAG图的拆点二分图的最大匹配数