先写一部分,持续到更新完。
A: 寒衣调
Description
Input
Output
求出熬制所成孟婆汤的药效b[i],每碗孟婆汤后以换行结尾。
Sample Input
5 11
2 7 5 3 9
3 7
9 8 5
Sample Output
10 6 4 3 1 5 3 2
题意:由题意可知,b[i]=a[0]*a[1]*...*a[i-1]*a[i+1]*...*a[n - 1],即b[i]等于除a[i]以外其他项的乘积。
解法:我们可以看到a[i]是一个32位数,如果我们直接按等式乘的话,连long long都会爆,我们知道(a*b)%m=(a%m*b%m)%m;所以我们可以计算这个值。
开两个数组来表示前i项和i+1到n项的模m的乘积。这样的操作就不会再爆long long了。
#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <map>
using namespace std;
typedef long long LL;
const int maxn=100005;
int n,m;
LL a[maxn];
LL b[maxn],c[maxn];
int main()
{
while(scanf("%d %d",&n,&m)!=EOF)
{
b[0]=1;c[n+1]=1;
for(int i=1;i<=n;i++)
{
scanf("%d",&a[i]);
a[i]%=m;
b[i]=(b[i-1]*a[i])%m;
}
for(int i=n;i>=1;i--)
c[i]=(c[i+1]*a[i])%m;
for(int i=1;i<n;i++)
{
printf("%lld ",(b[i-1]*c[i+1])%m);
}
printf("%lld
",b[n-1]);
}
return 0;
}
/**********************************************************************
Problem: 1163
User: jk1601zr
Language: C++
Result: AC
Time:428 ms
Memory:4368 kb
**********************************************************************/
B: 漫漫上学路
Description
对于csuxushu来说,能够在CSU(California State University)上学是他一生的荣幸。CSU校园内的道路设计的十分精巧,由n+1条水平道路和n+1条竖直道路等距交错而成,充分体现了校园深厚的文化底蕴。然而不幸的是CS市每到夏季,天降大雨,使得CSU常常形成“CS海”的奇观,今年,也就是2016年同样也不例外,校园有一半的区域被淹了。
由于要进行一年一度激动人心的省赛选拔了,起迟了的csuxushu赶紧从寝室背着一包模板前往机房,好奇的csuxushu发现虽然道路被淹了,但是只有左上三角区域受到影响,也就是说他可以在副对角线以下的道路畅通行走。在这个惊人的场景下,csuxushu做了一个惊人的决定,他要算出他有多少种前往机房的最短路线。然而只有10分钟了,这时候他想到了你——全CSU最厉害的程序员来帮助他解决这个问题。
需要指出的是CSU可以看做左下顶点为csuxushu的寝室(0,0),右上顶点为机房(n,n)的方形区域。
Input
多组数据。每组数据只有一行,为一个整数n(1 ≤n ≤30)。
Output
每组数据输出一行,即由寝室到机房的最短路线方案数。测试数据保证结果为64位整数。
Sample Input
4
Sample Output
14
题意:求点(0,0)到点(n,n)最短路线方案有多少种,那么每一步肯定是向右和向上走,
可以利用dp的思想,假如我们记一个ans[i][j]表示到坐标(i,j)的方案数,则ans[i][j]=ans[i][j-1](假如此坐标不合法则为0)+ans[i-1][j](假如此坐标不合法则为0)
#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <map>
using namespace std;
typedef long long LL;
const int maxn=105;
int n,m;
LL dp[maxn][maxn];
int main()
{
while(scanf("%d",&n)!=EOF)
{
memset(dp,0,sizeof(dp));
dp[0][0]=1;
for(int i=1;i<=n;i++)
{
for(int j=0;j<=i;j++)
{
if(j==0)
dp[i][j]=dp[i-1][j];
else
{
if(i==j)
dp[i][j]=dp[i][j-1];
else
dp[i][j]=dp[i][j-1]+dp[i-1][j];
}
}
}
printf("%lld
",dp[n][n]);
}
return 0;
}
/**********************************************************************
Problem: 1772
User: jk1601zr
Language: C++
Result: AC
Time:4 ms
Memory:2108 kb
**********************************************************************/
C: Use FFT
Description
Bobo computes the product P(x)⋅Q(x)=c0 + c1x + … + cn + mxn + m for two polynomials P(x)=a0 + a1x + … + anxn and Q(x)=b0 + b1x + … + bmxm. Find (cL + cL + 1 + … + cR) modulo (109 + 7) for given L and R.
- 1 ≤ n, m ≤ 5 × 105
- 0 ≤ L ≤ R ≤ n + m
- 0 ≤ ai, bi ≤ 109
- Both the sum of n and the sum of m do not exceed 106.
Input
The input consists of several test cases and is terminated by end-of-file.
The first line of each test case contains four integers n, m, L, R.
The second line contains (n + 1) integers a0, a1, …, an.
The third line contains (m + 1) integers b0, b1, …, bm.
Output
For each test case, print an integer which denotes the reuslt.
Sample Input
1 1 0 2
1 2
3 4
1 1 1 2
1 2
3 4
2 3 0 5
1 2 999999999
1 2 3 1000000000
Sample Output
21 18 5
题意:FFT?不太会啊。但实际上这是个骗局,这题根本就用不到FFT,这个是我们之前学习过的多项式的乘法,
 我们只要对b求前缀和,用a1-an去乘它就行了。
我们只要对b求前缀和,用a1-an去乘它就行了。#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int maxn=500005;
const int MOD=1000000007;
int n,m,l,r;
int a[maxn],b[maxn];
int main()
{
while(scanf("%d %d %d %d",&n,&m,&l,&r)!=EOF)
{
for(int i=0;i<=n;i++)
scanf("%d",&a[i]);
for(int i=0;i<=m;i++)
scanf("%d",&b[i]);
LL sum=0,ans=0;
for(int i=l;i<=r&&i<=m;i++)
sum=(sum+(LL)b[i])%MOD;
for(int i=0;i<=n;i++)
{
ans=(ans+a[i]*sum)%MOD;
l--;
if(l>=0&&l<=m)
sum=(sum+b[l])%MOD;
if(r>=0&&r<=m)
sum=(sum-b[r]+MOD)%MOD;
r--;
}
printf("%lld
",ans);
}
return 0;
}
/**********************************************************************
Problem: 2173
User: jk1601zr
Language: C++
Result: AC
Time:608 ms
Memory:5928 kb
**********************************************************************/
D: sequence
Description
给出一个长度为N的正整数序列a,你有两种变换操作:
1.把数列中的某个数乘 2。
2.把数列中的所有数减 1。
现在你需要通过最少的变换操作把这个数列中的数全部变成 0。
Input
第一行一个N。下面 N 行,每行一个正整数 Ai 描述这个数列。1 < =n < =200000, 1 < =ai < =109
Output
输出一行一个正整数,表示最少的变换次数。
Sample Input
2
1
2
Sample Output
3
题意:给你两种操作,使得最后使得所有的数都为0,求最少的变化次数。
解法:本来理解题意有点问题,数一直减下去是会小于0的,第一时间以为变为0,就可以不用管了。所以所有数减1的次数肯定是最大的那个数,其他的数在减1的过程中通过乘2的变化使得与最大的数相同,然后一起减1使得所有的数都为0
那么就是要求乘2的次数,其实仔细想一想,乘2的次数只需要满足在开始的值的时候乘以2大于最大的值的次数即可。
#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <map>
using namespace std;
typedef long long LL;
const int maxn=200005;
int n,m;
int a[maxn];
int fun(int x)
{
int cnt=0;
while(x<m)
{
cnt++;
x=2*x;
}
return cnt;
}
int main()
{
while(scanf("%d",&n)!=EOF)
{
m=0;
for(int i=1;i<=n;i++)
{
scanf("%d",&a[i]);
m=max(m,a[i]);
}
int ans=m;
for(int i=1;i<=n;i++)
{
ans+=fun(a[i]);
}
printf("%d
",ans);
}
return 0;
}
/**********************************************************************
Problem: 2046
User: jk1601zr
Language: C++
Result: AC
Time:84 ms
Memory:2804 kb
**********************************************************************/
E: 身份证号
Description
在中华人民共和国,每位公民都有一个唯一的身份证号码。中华人民共和国的居民身份证号码由 17 位本体码和 1 位校验码组成。17 位的本体码由三部分组成:地址码、出生日期码和顺序码。其中地址码占 6 位、出生日期码占 8 位、顺序码占 3 位。顺序码的奇数分配给男性,偶数分配给女性,同时顺序码的 3 位不能为全 0。出生日期码的前 4 位表示出生年份,接下来 2 位表示出生月份,最后两位表示出生日期。考虑到实际的情况,我们约定出生日期必须在 1900 年 1 月 1 日到 2011 年 12 月 31 日的范围内,并且对于闰年的 2 月有 29 日。 最后对于地址码,它表示所属的行政区划,输入文件中会给出对于该测试点所有可行的地址码。1 位的校验码是根据前面 17 位计算得出的。将本体码从左到右用a1,a2…a17表示,校验码用x表示,则下面的关系成立
其中0 <=x<=10,如果x=10,就用大写英文字母表示。
按照前面的规定,可以验证 11010519491231002X 是一个合法的女性身份证号码(110105 是北京市朝阳区的地址码)。现在要你写一个程序验证给定的身份证号码是否合法,并且对于合法的身份证,给出这位公民的性别。
注意:能被 4 整除的非整百年或能被 400 整除的年份称为闰年。例如 2004 年、 2000 年是闰年, 1900 年、 2003年不是闰年。
Input
第一行包含两个正整数M,N 1<=M<=4000 第二行包含M个长度为 6 的数字串, 表示该测试点中可行的地址码,地址码保证第一位数字非 0。 下面包含N行,每行给出一个长度为 18 的字符串,其中前 17 位为 0 到 9 的数字,第 18 位为 0 到 9 的数字或大写字母X
Output
共N行,第i行表示对于第i个输入号码的判断结果。Invalid 表示不合法, Male 表示合法并且为男性, Female 表示合法并且为女性。
Sample Input
2 3
110105 320102
11010519491231002X
320102199502091613
110105198312310013
Sample Output
Female Male Invalid
题意:模拟
解法:先判断前面的地区位是否是正确可取的,然后判断年月日是否是正确的,然后求sum值看模11结果是否为1,上述都满足就判断16位是奇数还是偶数。
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int maxn=100005;
int n,m;
set<string>ss;string s;
int monthday[13]={0,31,28,31,30,31,30,31,31,30,31,30,31};
int main()
{
scanf("%d %d",&m,&n);
for(int i=0;i<m;i++)
{
cin>>s;
ss.insert(s);
}
for(int i=0;i<n;i++)
{
cin>>s;
string temp="";
for(int j=0;j<6;j++)
temp+=s[j];
// cout<<temp<<endl;
if(ss.count(temp)==0)
{
printf("Invalid
");
// cout<<1<<endl;
continue;
}
int year=(s[6]-'0')*1000+(s[7]-'0')*100+(s[8]-'0')*10+s[9]-'0';
int month=(s[10]-'0')*10+s[11]-'0';
int day=(s[12]-'0')*10+s[13]-'0';
if(year%4==0&&year%100!=0||year%400==0)
monthday[2]=29;
if(month<1||month>12||day<0||day>monthday[month])
{
printf("Invalid
");
// cout<<2<<endl;
continue;
}
int sum=0;
for(int i=0;i<17;i++)
sum+=((s[i]-'0')*(1<<(17-i)))%11;
if(s[17]=='X')
sum+=10;
else
sum+=(s[17]-'0');
if(sum%11!=1)
{
printf("Invalid
");
// cout<<3<<endl;
continue;
}
if((s[16]-'0')%2)
printf("Male
");
else
printf("Female
");
}
return 0;
}
/**********************************************************************
Problem: 2043
User: jk1601zr
Language: C++
Result: AC
Time:4 ms
Memory:2028 kb
**********************************************************************/
F: 象棋
Description
車是中国象棋中的一种棋子,它能攻击同一行或同一列中没有其他棋子阻隔的棋子。一天,小度在棋盘上摆起了许多車……他想知道,在一共N×M个点的矩形棋盘中摆最多个数的車使其互不攻击的方案数。他经过思考,得出了答案。但他仍不满足,想增加一个条件:对于任何一个車A,如果有其他一个車B在它的上方(車B行号小于車A),那么車A必须在車B的右边(車A列号大于車B)。
现在要问问你,满足要求的方案数是多少 。
Input
第一行一个正整数T,表示数据组数。( T<=10)
对于每组数据:一行,两个正整数N和M(N<=100000,M<=100000)。
Output
对于每组数据输出一行,代表方案数模1000000007(10^9+7)。
Sample Input
1
1 1
Sample Output
1
题意:我们考虑考虑N<=M的情形,那么最大放置数就是N个
事实上,由于每一列只能放一个,所以我们可以用每一行中棋子所放置的列来记录当前位置,因此得到一个排列{aN},并且满足:a1<a2<...<aN-1<aN,并且可知{aN}的个数即为所求
从M个数中抽取出N个数,有C(M,N)中选择方法,抽取出来后,按照升序排列,故排列是可以与上述的一个{aN}一一对应的,为此,总共所需的方案数是C(M,N),但是这个值比较大,利用Lucas解就行。
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int p=1000000007;
const int maxn=200005;
int T;
int n,m;
LL quick_mod(LL a,LL b)
{
LL ans=1;
a%=p;
while(b)
{
if(b&1)
{
ans=ans*a%p;
b--;
}
b>>=1;
a=a*a%p;
}
return ans;
}
LL C(LL n,LL m)
{
LL ans=1;
for(int i=1;i<=m;i++)
{
LL a=(n+i-m)%p;
LL b=i%p;
ans=ans*(a*quick_mod(b,p-2)%p)%p;
}
return ans;
}
LL Lucas(LL n, LL m)
{
if(m==0)
return 1;
return C(n%p,m%p)*Lucas(n/p,m/p)%p;
}
int main()
{
scanf("%d",&T);
while(T--)
{
scanf("%d %d",&n,&m);
if(n>m)
swap(n,m);
printf("%lld
",Lucas(m,n));
}
return 0;
}
/**********************************************************************
Problem: 2049
User: jk1601zr
Language: C++
Result: AC
Time:68 ms
Memory:2024 kb
**********************************************************************/
G: 小M的移动硬盘
Description
最近小M买了一个移动硬盘来储存自己电脑里不常用的文件。但是他把这些文件一股脑丢进移动硬盘后,觉得这些文件似乎没有被很好地归类,这样以后找起来岂不是会非常麻烦?
小M最终决定要把这些文件好好归类,把同一类地移动到一起。所以现在小M有了这几种操作:
1 u 表示把编号为u的文件放到最上面
2 u 表示把编号为u的文件放到最下面
3 u v 表示把编号为u的文件放到编号为v的文件的后面
已知在最开始的时候,1号文件到n号文件从上往下排布
现在小M已经给出了他所进行的所有操作,你能告诉他操作之后的序列是会变成什么样子吗?
Input
第一行为一个数字T(T<=10)表示数据组数
第二行为两个数字n、m(1<=n,m<=300000)表示序列长度和小M的操作次数
接下来m行每行两个或三个数字,具体含义见题面
保证数据合法
Output
输出一行表示小M操作结束后的序列
Sample Input
1
10 5
1 5
2 3
2 6
3 4 8
3 1 3
Sample Output
5 2 7 8 4 9 10 3 1 6
用数组模拟双向队列,细节的东西可以看紫书上
#include <iostream>
#include <cstdio>
#include <string>
#include <string.h>
#include <queue>
#include <vector>
#include <stack>
#include <set>
#include <algorithm>
using namespace std;
#define ll long long
const int maxn = 300005;
int n;
int m;
int leftt[maxn];
int rightt[maxn];
int flag;
int a, b;
void init()
{
rightt[0] = 1;
leftt[n + 1] = n;
for (int i = 1; i <= n; i++)
{
leftt[i] = i - 1;
rightt[i] = i + 1;
}
}
void link(int l, int r)
{
rightt[l] = r;
leftt[r] = l;
}
int main()
{
int T;
cin >> T;
while (T--)
{
cin >> n >> m;
init();
for (int i = 0; i < m; i++)
{
cin >> flag;
if (flag == 1)
{
cin >> a;
if(rightt[0]==a)
continue;
int la = leftt[a];
int ra = rightt[a];
int r0 = rightt[0];
link(la, ra);
link(a, r0);
link(0, a);
}
else if (flag == 2)
{
cin >> b;
if(leftt[n+1]==b)
continue;
int lb = leftt[b];
int rb = rightt[b];
int ln = leftt[n + 1];
link(lb, rb);
link(ln, b);
link(b, n + 1);
}
else
{
cin >> a >> b;
if(rightt[b]==a)
continue;
int la = leftt[a];
int ra = rightt[a];
int rb = rightt[b];
link(la, ra);
link(a, rb);
link(b, a);
}
}
int temp = rightt[0];
cout << temp;
while (rightt[temp] != (n + 1))
{
cout << " "<< rightt[temp] ;
temp = rightt[temp];
}
cout<<endl;
}
return 0;
}
/**********************************************************************
Problem: 1982
User: jk1601zr
Language: C++
Result: AC
Time:968 ms
Memory:4368 kb
**********************************************************************/
I: 驱R符
Description
阴阳师中有三中稀有度的式神R,SR,SSR,其中R的稀有度最低,每次抽符,会随机得到一种式神,然而子浩君对R式神已经深恶痛绝。
某天,子浩君突然发现,有一种护身符,叫做驱R符,为什么会驱R?因为很多的R式神有密集恐惧症,而这个符上有很多的交点。
驱R符主体是一个圆环构成,圆周上面有n个位置可以绑上细线,可以这样把n个位置两两连接,然后在这个圆上产生很多的交点。
现在,子浩君想要做一个驱R符,他想知道,如果他现在的圆上有n个绑定细线的位置(位置可以由子浩君改动)的话,最多可以产生多少交点,以达到最好的驱R效果?
Input
第一行为测试数据数T(1<=T<=100000)
接下来是T行,每行有一个数字n(1<=n<=50000)
Output
对于每一个n,输出一行数字,代表最多可以产生的交点
Sample Input
5
1
2
3
4
5
Sample Output
0 0 0 1 5
题意:圆上有n个点,两两相连,求最多可以产生多少交点。
解法:画下图就知道,每四个不同点的点产生一个新点,交点最多的话就是这些新点不重复。那么结果也就是n*(n-1)*(n-2)*(n-3)/24,注意会爆long long。
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int maxn=100005;
LL n,m;
int main()
{
int T;
scanf("%d",&T);
while(T--)
{
scanf("%lld",&n);
if(n<=3)
{
printf("0
");
continue;
}
LL temp=n*(n-1)*(n-2)*(n-3)/24;
printf("%lld
",temp);
}
return 0;
}
/**********************************************************************
Problem: 1985
User: jk1601zr
Language: C++
Result: AC
Time:76 ms
Memory:2024 kb
**********************************************************************/
J: 神奇药水
Description
对于csuxushu来说,能够在CSU(California State University)组织2017年的ACM暑期集训让他感到十分荣幸。 csuxushu是一名充满梦想的程序员,因此他也希望来参加暑期集训的ACM萌新们和他一样怀揣着书写CSU-ACM历史的梦想。 一个偶然的机会,他在机房的某个角落得到了一本来自远古神犇的药水配方秘籍。秘籍上记载了许多AC药水配方,每一种药水都需要用两种原料 <勤奋,聪明> 按一定的比例配置而成。
“只要萌新喝下这些药水,他们的实力将有质的提升!”
——《远古AC药水秘籍》
此刻萌新们正在机房内和题目奋战,耳边的WA声不绝于耳。此情此景,csuxushu下定决心要为萌新们配置这些药水。 但是这两种原料市面上并不出售,因此只能由一些已有药水混合而成。为此他四处搜寻,机房不时放进新的药水和运出药水,并且在机房内的每种药水量都保证足够多。作为全CSU最聪明的程序员,对于每一个神奇药水配方,你能告诉他能否配成吗?
Input
多组数据。
对于每组数据,第一行一个整数N(1 < =N < =105),代表操作数。
接下来N行,每行一个三元组(K, X, Y) ,XX 和 YY 分别代表勤奋和聪明两种原料在药水中的浓度,其中 XX% + YY% = 100% 。
K = 0 :询问是否可以配置神奇药水(X, Y) ;
K = 1 :新增一种原料药水(X, Y) ;
K = −1 :删除所有原料药水(X, Y) ,如果没有这种药水则忽略此操作;
Output
对于每个K = 0 的询问输出一行,Yes或No。
Sample Input
6
1 65.00 35.00
0 93.58 6.42
1 44.64 55.36
1 68.27 31.73
0 54.36 45.64
0 46.04 53.96
Sample Output
No Yes Yes
题意:给你一定数量的浓度不一定药剂,然后配置一个浓度一定的药剂,看是否能配置成功。
解法:我们知道配置的话,只要在最小浓度和最大浓度范围之内,给定的浓度都能配置到。所以利用set的自动排序直接用set存储药剂的x浓度值,每次要配置的话就看下是否大于最小值小于最大值。
注意的点呢:要注意每次set要clear,并且在判断最小最大值的时候要判断set是否empty。不然你会收获wa和re。
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int maxn=100005;
int n,k;
double x,y;
set<double>s;
int main()
{
while(scanf("%d",&n)!=EOF)
{
s.clear();
for(int i=0;i<n;i++)
{
scanf("%d %lf %lf",&k,&x,&y);
if(k==1)
s.insert(x);
else if(k==0)
{
if(s.empty())
printf("No
");
// cout<<*s.begin()<<" "<<*s.end()<<endl;
else if((*s.begin())<=x&&(*(--s.end()))>=x)
printf("Yes
");
else
printf("No
");
}
else if(k==-1)
s.erase(x);
}
}
return 0;
}
/**********************************************************************
Problem: 1974
User: jk1601zr
Language: C++
Result: AC
Time:132 ms
Memory:2160 kb
**********************************************************************/
K: Bit-reversal Permutation
Description
A fast Fourier transform (FFT) algorithm computes the discrete Fourier transform (DFT) of a sequence, or its inverse (IFFT). Fourier analysis converts a signal from its original domain (often time or space) to a representation in the frequency domain and vice versa. An FFT rapidly computes such transformations by factorizing the DFT matrix into a product of sparse (mostly zero) factors. As a result, it manages to reduce the complexity of computing the DFT from O(n2), which arises if one simply applies the definition of DFT, to O(nlogn), where n is the data size.
——From Wikipedia
During this summer holiday, csuxushu feels so bored to learn FFT. Because FFT is a complicated algorithm, he need to apply a bit-reversal permutation to a sequence first before DFT which is a part of FFT.
In applied mathematics, a bit-reversal permutation is a permutation of a sequence of n items, where n = 2^k is a power of two. It is defined by indexing the elements of the sequence by the numbers from 0 to n − 1 and then reversing the binary representations of each of these numbers (padded so that each of these binary numbers has length exactly k). Each item is then mapped to the new position given by this reversed value.
Because all fellows in CSU(California State University ) can apply FFT, NTT or even FWT, it is a shame that he even doesn't know how to take the first step. As one of the best computer programmer in CSU, can you help him?
You may think this problem is too hard to solve. In fact, it is a piece of cake to you. Remember to see the hint :-)
Input
The first line of the input gives the number of test cases T(T≤10); T test cases follow.Each test case contains a number sequence.
In each case, the first line is a number N(1≤N≤10^5), the number of elements in the following sequence.The second line is the sequence.Its length may not be exactly a power of two, so you can append some zeros to make it the minimal power of two larger than or equal to N.
Output
For each test case, output the sequence from input in bit-reversal order.
Sample Input
1
6
21 58 96 12 45 65
Sample Output
21 45 96 0 58 65 12 0
Hint
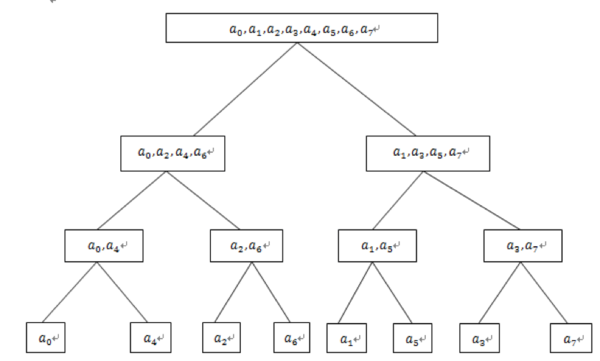
题意:给你一个序列,按照一个特定的要求输出序列,解法很简单,但一定要看Hint!!!,看着这个图,写dfs就行。
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int maxn=1000005;
int T,n,m;
int a[maxn],b[maxn];
void dfs(int l,int r)
{
if(l>=r)
return;
int mid=(l+r)/2;
int pos1=l,pos2=mid+1;
for(int i=l;i<=r;i++)
{
if(i%2==0)
b[pos1++]=a[i];
else
b[pos2++]=a[i];
}
for(int i=l;i<=r;i++)
a[i]=b[i];
dfs(l,mid);
dfs(mid+1,r);
}
int main()
{
scanf("%d",&T);
while(T--)
{
memset(a,0,sizeof(a));
scanf("%d",&n);
for(int i=0;i<n;i++)
scanf("%d",&a[i]);
m=0;
while(pow(2,m)<n)
m++;
m=pow(2,m) - 1;
// cout<<m<<endl;
dfs(0,m);
for(int i=0;i<m;i++)
printf("%d ",a[i]);
printf("%d
",a[m]);
}
return 0;
}
/**********************************************************************
Problem: 1977
User: jk1601zr
Language: C++
Result: AC
Time:344 ms
Memory:10020 kb
**********************************************************************/
L: 不堪重负的树
Description
小X非常喜欢树,然后他生成了一个大森林给自己玩。
玩着玩着,小X陷入了沉思。
- 一棵树由N个节点组成,编号为i的节点有一个价值Wi。
- 假设从树根出发前往第i个节点(可能是树根自己),一共需要经过Di个节点(包括起点和终点),那么这个节点对这棵树产生的负担就是Di与Wi的乘积。
- 对于一棵树而言,这棵树的负担值为所有节点对它产生的负担之和。
小X学习了dfs,如果他知道树的结构,他当然可以很容易地算出树的负担值。可是现在沉思中的小X并不知道树的结构形态,他只知道一棵二叉树的中序遍历以及每个节点的价值,那么这棵二叉树可能的最小负担值是多少呢?
Input
第一行为一个正整数T(T≤20)表示数据组数。
每组数据包括三行。
第一行为一个正整数N(N≤200)。
第二行为N个正整数Wi(Wi≤108),表示编号为i的节点的价值。
第三行为N个正整数Pi(Pi≤N),为一个1~N的排列,表示二叉树的中序遍历结果。
Output
对于每组数据,输出一行一个正整数,表示这棵树可能的最小负担值。
Sample Input
2
4
1 2 3 4
1 2 3 4
7
1 1 1 1 1 1 1
4 2 3 5 7 1 6
Sample Output
18 17
区间dp了解一下?
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int INF=0x3f3f3f3f;
const int maxn=1005;
int T,n,m;
LL sum[maxn],dp[maxn][maxn],a[maxn],b[maxn],c[maxn];
int main()
{
scanf("%d",&T);
while(T--)
{
memset(dp,INF,sizeof(dp));
scanf("%d",&n);
for(int i=1;i<=n;i++)
scanf("%lld",&a[i]);
for(int i=1;i<=n;i++)
scanf("%lld",&b[i]);
for(int i=1;i<=n;i++)
c[i]=a[b[i]];
for(int i=1;i<=n;i++)
sum[i]=sum[i-1]+c[i];
for(int i=1;i<=n;i++)
dp[i][i]=c[i];
for(int j=2;j<=n;j++)
{
for(int i=j-1;i>0;i--)
{
dp[i][j]=min(dp[i][j-1],dp[i+1][j])+sum[j]-sum[i-1];
for(int k=i+1;k<j;k++)
dp[i][j]=min(dp[i][j],dp[i][k-1]+sum[j]-sum[i-1]+dp[k+1][j]);
}
}
printf("%lld
",dp[1][n]);
}
return 0;
}
/**********************************************************************
Problem: 1980
User: jk1601zr
Language: C++
Result: AC
Time:164 ms
Memory:9944 kb
**********************************************************************/
M: Polyline Simplification
Description
Mapping applications often represent the boundaries of countries, cities, etc. as polylines, which are connected sequences of line segments. Since fine details have to be shown when the user zooms into the map, these polylines often contain a very large number of segments. When the user zooms out, however, these fine details are not important and it is wasteful to process and draw the polylines with so many segments. In this problem, we consider a particular polyline simplification algorithm designed to approximate the original polyline with a polyline with fewer segments.
A polyline with n segments is described by n + 1 points p0=(x0,y0),...,pn=(xn,yn)p0=(x0,y0),...,pn=(xn,yn), with the ith line segment being pi−1pi. The polyline can be simplified by removing an interior point pi(1≤i≤n−1)pi(1≤i≤n−1), so that the line segments pi−1pipi−1pi and pipi + 1 are replaced by the line segment pi − 1pi + 1. To select the point to be removed, we examine the area of the triangle formed by pi−1,pi,andpi+1pi−1,pi,andpi+1 (the area is 0 if the three points are colinear), and choose the point pi such that the area of the triangle is smallest. Ties are broken by choosing the point with the lowest index. This can be applied again to the resulting polyline, until the desired number m of line segments is reached.
Consider the example below.

The original polyline is shown at the top. The area of the triangle formed by p2,p3,andp4p2,p3,andp4 is considered (middle), and p3p3 is removed if the area is the smallest among all such triangles. The resulting polyline after p3p3 is removed is shown at the bottom.
Input
The first line of input contains two integers n(2≤n≤200000)n(2≤n≤200000) and m(1≤m<n)m(1≤m<n). The next n + 1 lines specify p0,...,pnp0,...,pn. Each point is given by its x and y coordinates which are integers between −5000 and 5000 inclusive. You may assume that the given points are strictly increasing in lexicographical order. That is, xi<xi+1xi<xi+1 , or xi=xi+1xi=xi+1 and yi<yi+1yi<yi+1 for all 0≤i<n0≤i<n .
Output
Print on the kth line the index of the point removed in the kth step of the algorithm described above (use the index in the original polyline).
Sample Input
10 7
0 0
1 10
2 20
25 17
32 19
33 5
40 10
50 13
65 27
75 22
85 17
Sample Output
1 9 6
题意:给出点集,构成曲折线,如下图,每两个线构成一个三角形,三点共线认为面积为零,每次删掉面积最小的三角形和其顶点,余下两点自动连接,直到剩下m+1个点,输出每次删除的点的编号。
模拟着去做,用一个set对于三角形面积进行排序,删除一个点后要更新它左右两个点的数据。
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int maxn=200005;
int n,m;
struct Node
{
int id,val;
bool operator<(const Node b)const
{
if(val==b.val)
return id<b.id;
else
return val<b.val;
}
};
Node temp;
int x[maxn],y[maxn];
int l[maxn],r[maxn];
int area[maxn];
set<Node>s;
int cal(int i)
{
int a=i,b=l[i],c=r[i];
return abs(x[a]*y[b]+x[b]*y[c]+x[c]*y[a]-x[a]*y[c]-x[b]*y[a]-x[c]*y[b]);
}
int main()
{
while(scanf("%d %d",&n,&m)!=EOF)
{
s.clear();
for(int i=0;i<=n;i++)
scanf("%d %d",&x[i],&y[i]);
r[0]=1;l[n]=n-1;
for(int i=1;i<n;i++)
{
temp.id=i;
r[i]=i+1;l[i]=i-1;
temp.val=area[i]=cal(i);
s.insert(temp);
}
set<Node>::iterator it;
int nn=n-m;
for(int i=1;i<=nn;i++)
{
it=s.begin();
s.erase(it);
int t=(*it).id;
// cout<<t<<endl;
l[r[t]]=l[t];
r[l[t]]=r[t];
if(l[t]!=0)
{
temp.id=l[t];temp.val=area[l[t]];
it=s.find(temp);
s.erase(it);
area[l[t]]=cal(l[t]);
temp.val=area[l[t]];
s.insert(temp);
}
if(r[t]!=n)
{
temp.id=r[t];temp.val=area[r[t]];
it=s.find(temp);
s.erase(it);
area[r[t]]=cal(r[t]);
temp.val=area[r[t]];
s.insert(temp);
}
printf("%d
",t);
}
}
return 0;
}
/**********************************************************************
Problem: 2116
User: jk1601zr
Language: C++
Result: AC
Time:400 ms
Memory:15304 kb
**********************************************************************/
N: Scientific Conference
Description
Functioning of a scientific conference is usually divided into several simultaneous sections. For example, there may be a section on parallel computing, a section on visualization, a section on data compression, and so on.
Obviously, simultaneous work of several sections is necessary in order to reduce the time for scientific program of the conference and to have more time for the banquet, tea-drinking, and informal discussions. However, it is possible that interesting reports are given simultaneously at different sections.
A participant has written out the time-table of all the reports which are interesting for him. He asks you to determine the maximal number of reports he will be able to attend.
Input
The first line contains the number 1 ≤ N ≤ 100000 of interesting reports. Each of the next N lines contains two integers Ts and Te separated with a space (1 ≤ Ts < Te ≤ 30000). These numbers are the times a corresponding report starts and ends. Time is measured in minutes from the beginning of the conference.
Output
You should output the maximal number of reports which the participant can attend. The participant can attend no two reports simultaneously and any two reports he attends must be separated by at least one minute. For example, if a report ends at 15, the next report which can be attended must begin at 16 or later.
Sample Input
5
3 4
1 5
6 7
4 5
1 3
Sample Output
3
题意:给n个区间,求最多不相交区间的数量。
解法:贪心,按结束时间排序,贪开始时间刚大于上一个结束时间的最小结束时间,依次贪到最后,得到结果。
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int maxn=100005;
int n;
struct Node
{
int sta,endd;
}node[maxn];
bool cmp(Node a,Node b)
{
return a.endd<b.endd;
}
int main()
{
while(scanf("%d",&n)!=EOF)
{
for(int i=0;i<n;i++)
scanf("%d %d",&node[i].sta,&node[i].endd);
sort(node,node+n,cmp);
int ans=1;
int i=1;
int temp=node[0].endd;
while(i<n)
{
if(node[i].sta>temp)
{
ans++;
temp=node[i].endd;
}
else
i++;
}
printf("%d
",ans);
}
return 0;
}
/**********************************************************************
Problem: 1065
User: jk1601zr
Language: C++
Result: AC
Time:76 ms
Memory:2804 kb
**********************************************************************/
P: The Big Escape
Description
There is a tree-like prison. Expect the root node, each node has a prisoner, and the root node is the only exit. Each node can accommodate a large number of prisoners, but each edge per minute only one prisoner can pass.
Now, the big escape begins, every prisoner wants to escape to the exit.Do you know when the last one escapes from the prison.
Input
There are lots of case.
For each test case.The first line contains two integers n,m(n<=100000, 1<=m<=n), which indicates the number of nodes and the root node.
The next n-1 lines describe the tree.
Output
For each test case, you output one line “Case #%d:%d”
Sample Input
10 2
1 2
2 3
2 4
2 5
1 6
5 7
3 8
2 9
2 10
Sample Output
Case #1:2
题意:给你一些点,每个点,除了root之外都有一个囚犯,一分钟,只能有一个人在一条边上跑,最后求最少时间所有的人都跑出去。
解法:利用并查集,保留深度(孩子的数量会加深深度)。
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int maxn=100005;
int n,m;
int fa[maxn],cnt[maxn];
int a,b;
void init()
{
for(int i=0;i<=n;i++)
{
fa[i]=i;
cnt[i]=1;
}
}
int findd(int x)
{
if(x==fa[x])
return fa[x];
else
return fa[x]=findd(fa[x]);
}
int main()
{
int casee=1;
while(scanf("%d %d",&n,&m)!=EOF)
{
init();
for(int i=1;i<n;i++)
{
scanf("%d %d",&a,&b);
if(a==m||b==m)
continue;
int faa=findd(a),fb=findd(b);
if(faa!=fb)
{
fa[faa]=fb;
cnt[fb]+=cnt[faa];
}
}
int ans=0;
for(int i=1;i<=n;i++)
{
if(i==m||fa[i]!=i)
continue;
else
ans=max(ans,cnt[i]);
}
printf("Case #%d:%d
",casee++,ans);
}
return 0;
}
/**********************************************************************
Problem: 1908
User: jk1601zr
Language: C++
Result: AC
Time:376 ms
Memory:2804 kb
**********************************************************************/