椭圆曲线在Fp域上的加密（python实现）

椭圆曲线加密（python实现）

• 最近在上现代密码学，对椭圆曲线进行了一番了解，进行了实现
• 椭圆曲线的基本原理可借鉴这篇博客

• 通过查阅书籍，整理了下加密原理，如下：

• 自己实现了一下，直接上代码

# -*- coding: utf-8 -*-
"""
ECC在Fp域上的加解密
"""


def get_inverse_element(value, max_value):
    """
    计算value在1-max_value之间的逆元
    """
    for i in range(1, max_value):
        if (i * value) % max_value == 1:
            return i
    return -1


def gcd_x_y(x, y):
    """
    计算最大公约数
    """
    if y == 0:
        return x
    else:
        return gcd_x_y(y, x % y)
    

def calculate_p_q(x1,y1,x2,y2, a, p):
    """
    计算p+q
    """
    flag = 1  # 定义符号位
    if x1 == x2 and y1 == y2:
        member = 3 * (x1 ** 2) + a  # 计算分子
        denominator = 2 * y1    # 计算分母
    else:
        member = y2 - y1
        denominator = x2 - x1 
        if member* denominator < 0:
            flag = 0
            member = abs(member)
            denominator = abs(denominator)
    
    # 将分子和分母化为最简
    gcd_value = gcd_x_y(member, denominator)
    member = int(member / gcd_value)
    denominator = int(denominator / gcd_value)
    # 求分母的逆元    
    inverse_value = get_inverse_element(denominator, p)
    k = (member * inverse_value)
    if flag == 0:
        k = -k
    k = k % p
    # 计算x3,y3
    x3 = (k ** 2 - x1 - x2) % p
    y3 = (k * (x1 - x3) - y1) % p
    # print("%d<=====>%d" % (x3, y3))
    return [x3,y3]
    

def get_order(x0, y0, a, b, p):
    """
    计算椭圆曲线的阶
    """
    # 计算-p
    x1 = x0
    y1 = (-1 * y0) % p
    temp_x = x0
    temp_y = y0
    n = 1
    while True:
        n += 1
        p_value = calculate_p_q(temp_x,temp_y, x0, y0, a, p)
        if p_value[0] == x1 and p_value[1] == y1:
            print("==========该椭圆曲线的阶为%d=========" % (n+1))
            return n+1
            
        temp_x = p_value[0]
        temp_y = p_value[1]

    # print("%d-%d-%d-%d" % (x0,y0,x1,y1))


def get_x0_y0_x1_y1(x0, a, b, p):
    """
    计算p和-p
    """
    y0 = -1
    for i in range(0,p):
        if i ** 2 % p == (x0**3 + a*x0 + b) % p:
            y0 = i
            break
    
    # 如果y0找不到则返回False
    if y0 == -1:
        return False
    # 计算-y
    x1 = x0
    y1 = -1 * y0 % p
    # print("%d-%d-%d-%d" % (x0,y0,x1,y1))
    return [x0,y0,x1,y1]


def draw_graph(a,b,p):
    """
    输出散列图
    """
    x_y = []
    for i in range(p):
        x_y.append(["-" for i in range(p)])
    
    for i in range(p):
        value = get_x0_y0_x1_y1(i, a, b, p)
        if value != False:
            x0 = value[0]
            y0 = value[1]
            x1 = value[2]
            y1 = value[3]
            # print("%d-%d-%d-%d" % (x0,y0,x1,y1))
            x_y[x0][y0] = 1
            x_y[x1][y1] = 1
    print("椭圆曲线的散列图为:")
    for j in range(p):
        if p-1-j >= 10:
            print(p-1-j, end=" ")
        else:
             print(p-1-j, end="  ")
        for i in range(p):
            print(x_y[i][p-j-1], end="  ")
        print()
    print("   ",end="")
    for i in range(p):
        if i >= 10:
            print(i, end=" ")
        else:
            print(i, end="  ")
        
    print()


def calculate_np(G_x, G_y, private_key, a, p):
    """
    计算nG
    """
    temp_x = G_x
    temp_y = G_y
    while private_key != 1:
        p_value = calculate_p_q(temp_x,temp_y, G_x, G_y, a, p)
        temp_x = p_value[0]
        temp_y = p_value[1]
        private_key -= 1
    return p_value
    
    
def ecc_encrypt_and_decrypt():
    while True:
        a = int(input("请输入椭圆曲线的参数a:"))
        b = int(input("请输入椭圆曲线的参数b:"))
        p = int(input("请输入椭圆曲线的参数p(p为质数):"))
        
        if (4*(a**3) + 27*(b**2)) % p ==0:
            print("选取的椭圆曲线不能用于加密，请重新选择
")
        else:
            break
    # 输出该椭圆曲线的散点图
    draw_graph(a,b,p)
    print("在上图中选出一个点作为生成元G")
    G_x = int(input("你选取的横坐标G_x:"))
    G_y = int(input("你选取的纵坐标G_y:"))
    # 获取该椭圆曲线的阶
    n = get_order(G_x, G_y, a, b, p)
    # 获取私钥并且key < 椭圆曲线的阶n
    private_key = int(input("输入私钥key(<%d):" % n))
    # 计算公钥 nG
    Q = calculate_np(G_x,G_y,private_key,a,p)
    print("==================生成公钥{a=%d,b=%d,p=%d,阶%d,G(%d,%d),Q(%d,%d)}======" % (a, b, p, n, G_x, G_y , Q[0], Q[1]))
    
    # 加密开始
    k = int(input("请给出整数(<%d):" % n))
    k_G = calculate_np(G_x,G_y,k,a,p) # 计算kG
    k_Q = calculate_np(Q[0],Q[1],k,a,p) # 计算kQ
    plain_text = int(input("请输入要加密的明文："))
    cipher_text = plain_text * k_Q[0]  # 计算明文与kQ横坐标的乘积
    # 密文为
    C = [k_G[0], k_G[1],cipher_text] 
    print("密文为：{(%d,%d),%d}" % (C[0], C[1], C[2]))
    # 解密
    # 计算private_key*kG
    decrypto_text = calculate_np(C[0],C[1],private_key,a,p) 
    
    inverse_value = get_inverse_element(decrypto_text[0], p)
    m = C[2] * inverse_value % p
    print("解密后的明文为%d" % m)

    
if __name__ == '__main__':
    ecc_encrypt_and_decrypt()

运行结果

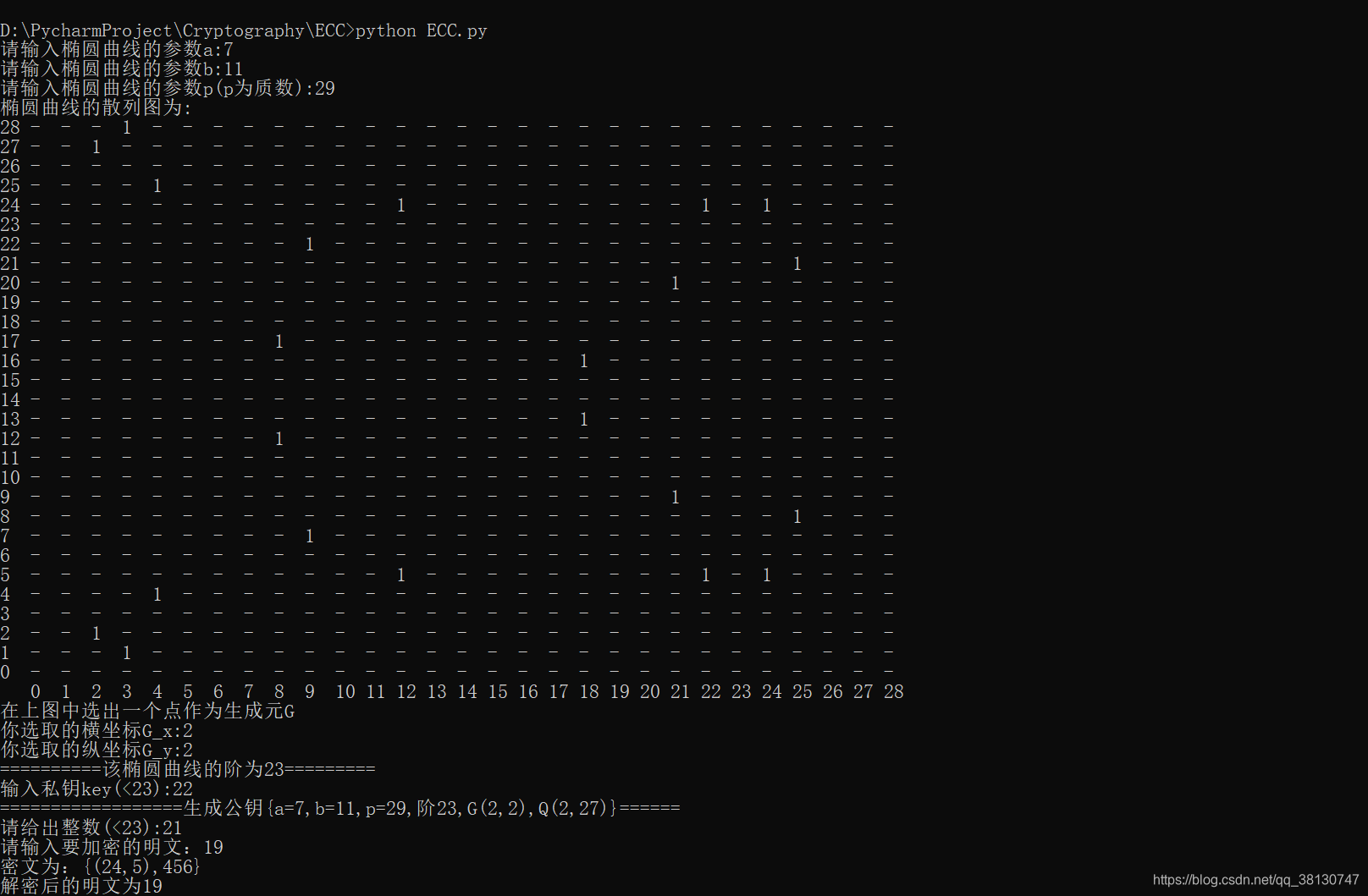
补充

• 实现过程中，发现斜率不好计算，因为是分数的原因，可以考虑这样计算，假定计算a/b（mod p）可以转换为a/b（mod p） = a * (b的逆元) （mod p）就会大大简化计算。
• 在编码的过程中，一方面为了使结果更加直观，方便演示，另一方面，因为选择的基点G，必须在椭圆曲线上，所以让椭圆曲线输出整个在Fp域上的点，但是当p取的很大时，就会出现一屏幕输出不下，Fp域，这个时候，可以放弃使用输出整个Fp域，通过计算得到一个点G。
• 在这个代码实现中，加解密稍微有点不一样，教材中
  加密时：
  选择明文M（x，y）为一个点，而非一个数，而密文为C = （kG，（M+kQ））。计算点C1=M+kQ和C2=kG
  解密时：
  M = C1-dC2
  数学原理为:C1-kC2=M+kQ-dkG=M+kdG-kG-M
  数学原来上能解密是因为:M = C1-dC2=M+kQ-dkG=M+kdG-dkG = M
  当明文为一个数m时，具体原理不变

博主是一枚进击的小白，难免有错误，如果发现或是有其他建议，请及时提出，进行商讨交流，在此感激不尽

如果对椭圆曲线原理不清楚，可以查看这篇博客，写的很详细。
参考链接
https://www.cnblogs.com/Kalafinaian/p/7392505.html