机器学习中的微分和矩阵

微积分选讲

• 极限
  一个函数在 x 附近的数就是极限
  

• 无穷小
  逼近的时候, 需要了解逼近的时候需要了解以什么样的速度来逼近无穷小.
  

• 微分和泰勒级数
  微分学的核心思想就是逼近, 通常而言我们研究的函数都是比较复杂的,我们想用一个简单的函数进行逼近, 不准的话, 我们想知道这个逼近有多近, 用一个线性函数俩逼近
  
  多变量就是用给一个平面去逼近一个曲面
  单变量就是用一条直线去逼近一个曲线

• 高阶导数
  不满足一条直线来逼近, 误差比较大, 我们可以进一步逼近, 将 o(x)进一步逼近, 随着求导的增加, 就会进一步的逼近, 当然也会得到更多的信息.
  

• 一元微分学的顶峰 泰勒级数
  用多项式逼近的方式描述高阶导数, 求很多次导数就可以
  
  连续不一定可导, 但可导一定连续

• 积分和微积分定理
  积分, 用极限的思想来定义积分, 我们要注重背后的意义是什么?
  求面积, 用已知的东西去逼近未知的东西, 微分和积分是逆运算
  
  

• 牛顿法
  优化问题, 对于一个无穷可微条件, 寻找局部最小值
  

1. 梯度下降法
   
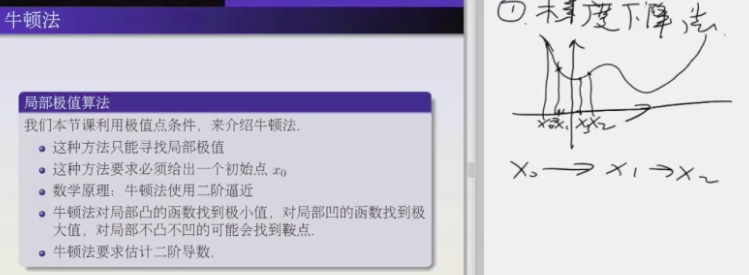
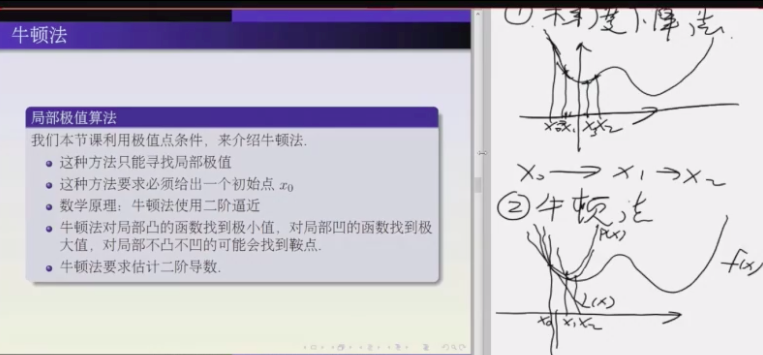
2. 牛顿法
   同样一个函数, 一阶逼近只是知道方向, 用二阶逼近, 抛物线有极小值, 用到抛物线的最小值调节步长, 大概知道走多远.
   

• 机器学习在做什么?
  通常数据离散的,
  统计机器学习---从数据到模型
  
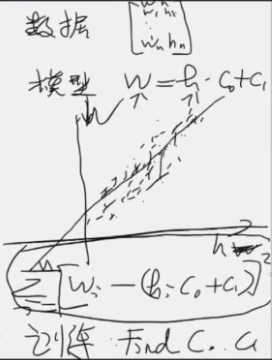
  模型是连续的, 数据是零散的, 通过定义一个损失函数, 来找到连续函数的参数, 也就是找到相关的系数.
  模型都是猜测, 然后再用数据来 fit 模型
• 参考资料