递归算法C++代码:
1 /** 2 * Definition for a binary tree node. 3 * struct TreeNode { 4 * int val; 5 * TreeNode *left; 6 * TreeNode *right; 7 * TreeNode(int x) : val(x), left(NULL), right(NULL) {} 8 * }; 9 */ 10 class Solution { 11 public: 12 vector<int> inorderTraversal(TreeNode* root) { 13 vector<int> tra; 14 Morder(root,tra); 15 return tra; 16 } 17 void Morder(TreeNode* root,vector<int> &tra){ 18 if(root==NULL) return; 19 if(root->left) 20 Morder(root->left,tra); 21 tra.push_back(root->val); 22 if(root->right) 23 Morder(root->right,tra); 24 } 25 };
非递归方法(迭代):通过stack容器
C++代码:O(n)空间复杂度,O(n)时间复杂度
自己写的,实际上为将递归方法代码用stack具体化,需要注意的是加上了回溯与向下递归的判别;
/** * Definition for a binary tree node. * struct TreeNode { * int val; * TreeNode *left; * TreeNode *right; * TreeNode(int x) : val(x), left(NULL), right(NULL) {} * }; */ /** 迭代法:具象描述递归执行过程 1)检查当前p是否为NULL,如果非NULL,当前节点入栈,只要当前节点有左子节点,左子节点入栈; 2)1之后,取栈顶元素p,由于1的操作,p没有左子节点,那么访问当前节点的值,且p出栈; 3)接下来访问右节点,p=p->right,如果右子节点存在,那么入栈,循环结束; **/ class Solution { public: vector<int> inorderTraversal(TreeNode* root) { if(root==NULL) return {}; vector<int>res; stack<TreeNode*>s; TreeNode*p=root; s.push(p); while(!s.empty()){ while(p&&p->left){ p=p->left;s.push(p); } p=s.top(); res.push_back(p->val);s.pop(); //此处先令p=p->right,p可用作第一个while判断是向下递归还是回溯,如果递归过程p为非空,如果为NULl则代表回溯,那么下一轮不用向左递归; p=p->right; if(p) s.push(p); } return res; } };
别人的代码:
1 /** 2 * Definition for a binary tree node. 3 * struct TreeNode { 4 * int val; 5 * TreeNode *left; 6 * TreeNode *right; 7 * TreeNode(int x) : val(x), left(NULL), right(NULL) {} 8 * }; 9 */ 10 class Solution { 11 public: 12 vector<int> inorderTraversal(TreeNode* root) { 13 //使用栈的非递归方法 14 vector<int> res; 15 stack<TreeNode*> st; 16 TreeNode* T=root; 17 while(T||!st.empty()){ 18 //将T的所有左孩子入栈 19 while(T){ 20 st.push(T); 21 T=T->left; 22 } 23 //访问T的元素,然后转到T的右孩子 24 if(!st.empty()){ 25 T=st.top(); 26 st.pop(); 27 res.push_back(T->val); 28 T=T->right; 29 } 30 } 31 return res; 32 } 33 };
方法三:Morris Traversal
由于需要用到Thread Binary Tree(线索二叉树),参考 透彻理解线索二叉树 彻底理解线索二叉树
Morris Traversal方法遍历二叉树(非递归,不用栈,O(1)空间)
对于n个节点的二叉树,左右孩子指针为2n个,利用的指针为n-1个,没有利用的指针为n+1个;利用空链域存储前驱和后继:
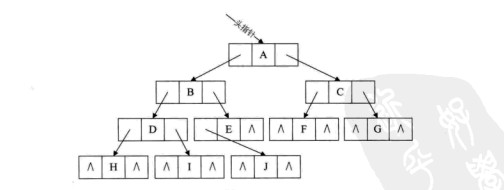
记ptr指向二叉链表中的一个结点,以下是建立线索的规则:
(1)如果ptr->lchild为空,则存放指向中序遍历序列中该结点的前驱结点。这个结点称为ptr的中序前驱;
(2)如果ptr->rchild为空,则存放指向中序遍历序列中该结点的后继结点。这个结点称为ptr的中序后继;
当然,Morris遍历只用到了线索二叉树的思想和部分操作,线索二叉树的更细节的东西此处不赘述。对于本题,实际上只用到了对叶节点的右指针的线索化,以及通过线索化的指针进行回溯。主要有以下两点:
#1 对所有叶节点的右指针的线索化,令其指向中序遍历的后继节点;
#2 通过线索化的节点,访问中序遍历的后继节点,并恢复被线索化的节点;
参考:二叉树的遍历:先序中序后序遍历的递归与非递归实现及层序遍历
C++代码如下:O(1)空间复杂度,O(n)时间复杂度
1 /** 2 * Definition for a binary tree node. 3 * struct TreeNode { 4 * int val; 5 * TreeNode *left; 6 * TreeNode *right; 7 * TreeNode(int x) : val(x), left(NULL), right(NULL) {} 8 * }; 9 */ 10 class Solution { 11 public: 12 vector<int> inorderTraversal(TreeNode* root) { 13 //Morris Traversal:右线索化+回溯 14 vector<int> res; 15 if(!root) return res; 16 TreeNode *p=root; 17 18 while(p){ 19 //定义两个节点指针变量p和p的左孩子pLeft 20 TreeNode *pLeft=p->left; 21 if(pLeft){ 22 //访问p的左孩子的最右子孩子(即pLeft右孩子的右孩子的右孩子...) 23 //线索化之前pLeft的最右子孩子的right指针指向NULL, 24 //线索化之后pLeft的最右子孩子的right指向中序遍历中该节点的后继节点p 25 //所以循环终止条件为pLeft->right==NULL 或 pLeft->right==p 26 while(pLeft->right && pLeft->right!=p){ 27 pLeft=pLeft->right; 28 } 29 //此时pLeft代表p的左孩子的最右子孩子 30 //pLeft->right==NULL代表没有被线索化,进行线索化然后访问p的左孩子 31 if(pLeft->right==NULL){ 32 pLeft->right=p; 33 p=p->left; 34 continue; 35 } 36 //pLeft->right!=NULL代表已经被线索化,此时已经回溯到原来的节点p(第2次访问),所以要恢复被线索化的pLeft的最右子孩子 37 else{ 38 pLeft->right=NULL; 39 } 40 } 41 res.push_back(p->val); 42 p=p->right;//访问右孩子(对非叶节点),回溯到中序遍历的后续节点(对叶节点); 43 //因为线索化的操作最终是对所有的叶节点进行的,所以上述语句实际有访问右孩子和回溯两个功能; 44 } 45 return res; 46 } 47 };