算法—基于堆的优先队列

1.具体算法

public class MaxPQ<Key> implements Iterable<Key> {
    private Key[] pq;                    //基于堆的完全二叉树
    private int N;                       // 存储于pq[1..N]中，pq[0]没有使用
    private Comparator<Key> comparator;  // optional Comparator

    
    public MaxPQ(int initCapacity) {
        pq = (Key[]) new Object[initCapacity + 1];
        N = 0;
    }
/**
     * 返回队列是否为空
     */
    public boolean isEmpty() {
        return N == 0;
    }

    /**
     * 返回优先队列中的元素个数
     */
    public int size() {
        return N;
    }

    /**
     * 返回最大元素
     */
    public Key max() {
        if (isEmpty()) throw new NoSuchElementException("Priority queue underflow");
        return pq[1];
    }
/**
     * 向优先队列中插入一个元素
     */
    public void insert(Key x) {

        // double size of array if necessary
        if (N >= pq.length - 1) resize(2 * pq.length);

        // add x, and percolate it up to maintain heap invariant
        pq[++N] = x;
        swim(N);
        assert isMaxHeap();
    }

    /**
     * 删除并返回最大元素
     */
    public Key delMax() {
        if (isEmpty()) throw new NoSuchElementException("Priority queue underflow");
        Key max = pq[1];//从根结点得到最大元素
        exch(1, N--);   //将其和最后一个结点交换
        sink(1);    //恢复堆的有序性
        pq[N+1] = null;     //防止越界
        if ((N > 0) && (N == (pq.length - 1) / 4)) resize(pq.length / 2);
        assert isMaxHeap();
        return max;
    }

private void swim(int k) {
        while (k > 1 && less(k/2, k)) {
            exch(k, k/2);
            k = k/2;
        }
    }

    private void sink(int k) {
        while (2*k <= N) {
            int j = 2*k;
            if (j < N && less(j, j+1)) j++;
            if (!less(k, j)) break;
            exch(k, j);
            k = j;
        }
    }
}

 2.算法分析

优先队列由一个基于堆的完全二叉树表示，存储于数组pq[1...N]中，pq[0]没有使用。在insert()中，我们将N加一并把新元素添加在数组最后，然后用swim()恢复堆的秩序。在delMax()中，我们从pq[1]中得到需要返回的元素，然后将pq[N]移动到pq[1]，将N减一并用sink()恢复堆的秩序。同时我们还将不再使用的pq[N+1]设为null，以便系统回收它所占用的空间。

命题：对于一个含有N个元素的基于堆的优先队列，插入元素操作只需不超过（lgN+1）次比较，删除最大元素的操作需要不超过2lgN次比较。

证明：由上一个命题可知，两种操作都需要在根结点和堆底之间移动元素，而路径的长度不超过lgN。对于路径上的每个结点，删除最大元素需要两次比较（除了堆底元素），一次用来找出较大的子结点，一次用来确定该子结点是否需要上浮。

对于需要大量混杂的插入和删除最大元素操作的典型应用来说，上面的命题意味着一个重要的性能突破。使用有序或是无序数组的优先队列的初级实现总是需要线性时间来完成其中一种操作，但基于堆的实现则能够保证在对数时间内完成它们。这种差别使得我们能够解决以前无法解决的问题。

堆上的优先队列操作如下图

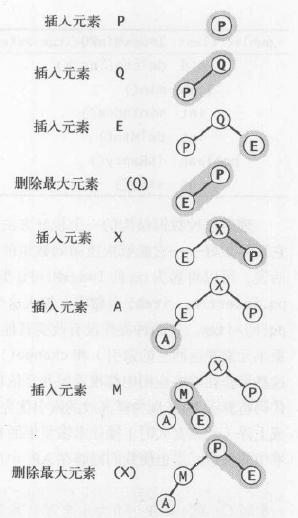
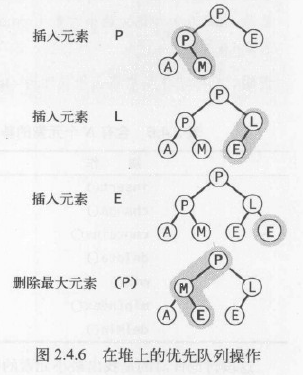
【源码下载】