我们可以把任意优先队列变成一种排序方法。将所有元素插入一个查找最小元素的优先队列,然后再重复调用删除最小元素的操作来将它们按顺序删去。用无序数组实现的优先队列这么做相当于进行一次插入排序。用基于堆的优先队列这样做等同于哪种排序?一种全新的排序方法!下面我们就用堆来实现一种经典而优雅的排序算法——堆排序。
堆排序可以分为两个阶段。在堆的构造阶段中,我们将原始数组重新组织安排进一个堆中;然后在下沉排序阶段,我们从堆中按递减顺序取出所有元素并得到排序结果。为了排序的需要,我们不再将优先队列的具体表示隐藏,并将直接使用swim()和sink()操作。这样我们在排序时就可以将需要排序的数组本身作为堆,因此无需任何额外空间。
1.堆的构造
由N个给定的元素构造一个堆有多难?我们当然可以在与NlogN成正比的时间内完成这项任务,只需从左至右遍历数组,用swim()保证扫描指针左侧的所有元素已经是一棵堆有序的完全树即可,就像连续向优先队列中插入元素一样。一个更聪明更高效的办法是从右至左用sink()函数构造子堆。数组的每个位置都已经是一个子堆的根结点了,sink()对于这些子堆也适用。如果一个结点的两个子结点都已经是堆了,那么在该结点上调用sink()可以将它们变成一个堆。这个过程会递归地建立起堆的秩序。开始时我们只需要扫描数组中的一半元素,因为我们可以跳过大小为1的子堆。最后我们在位置1上调用sink()方法,扫描结束。
命题:用下沉操作由N个元素构造堆只需少于2N次比较以及少于N次交换。
证明:观察可知,构造过程中处理的堆都较小。例如,要构造一个127个元素的堆,我们会处理32个大小为3的堆,16个大小为7的堆,8个大小为15的堆,4个大小为31的堆,2个大小为63的堆和1个大小为127的堆,【根据命题:删除最大元素的操作需要不超过2lgN次比较和lgN次交换】因此(最坏情况下)需要32*1+16*2+8*3+4*4+2*5+1*6=120次交换(两倍于比较)。
2.具体算法
/**
* 算法2.7 堆排序
* Created by huazhou on 2015/11/23.
*/
public class Heap extends Model {
public void sort(Comparable[] pq) {
int N = pq.length;
for (int k = N/2; k >= 1; k--)
sink(pq, k, N);
while (N > 1) {
exch(pq, 1, N--);
sink(pq, 1, N);
}
}
private void sink(Comparable[] pq, int k, int N) {
while (2*k <= N) {
int j = 2*k;
if (j < N && less(pq, j, j+1)) j++;
if (!less(pq, k, j)) break;
exch(pq, k, j);
k = j;
}
}
private boolean less(Comparable[] pq, int i, int j) {
return pq[i-1].compareTo(pq[j-1]) < 0;
}
protected void exch(Comparable[] pq, int i, int j) {
Comparable swap = pq[i-1];
pq[i-1] = pq[j-1];
pq[j-1] = swap;
}
}
这段代码用sink()方法将a[1]到a[N]的元素排序(sink()被修改过,以a[]和N作为参数)。for循环构造了堆,然后while循环将最大的元素a[1]和a[N]交换并修复了堆,如此重复直到堆变空。将exch()和less()的实现中的索引减一即可得到和其他排序算法一致的实现(将a[0]至a[N-1]排序)。

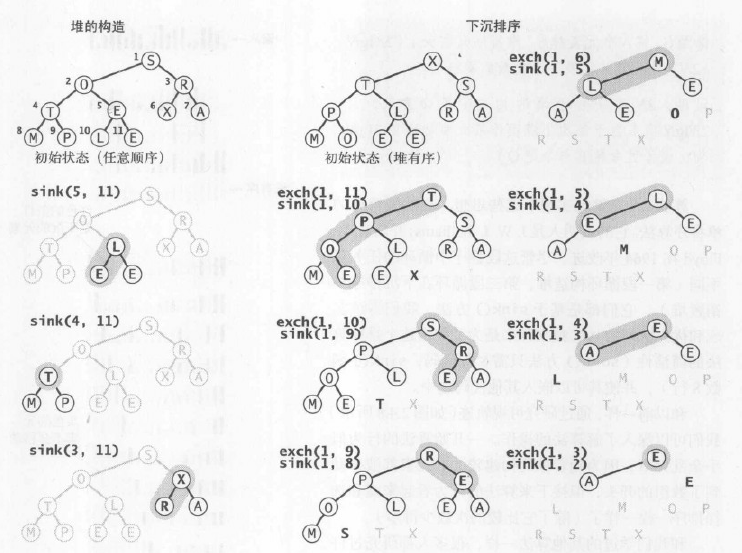

3.下沉排序
堆排序的主要工作都是在第二阶段完成的。这里我们将堆中的最大元素删除,然后放入堆缩小后数组中空出的位置。这个过程和选择排序有些类似(按照降序而非升序取出所有元素),但所需的比较要少得多,因为堆提供了一种从未排序部分找到最大元素的有效方法。
命题:将N个元素排序,堆排序只需少于(2NlgN+2N)次比较(以及一半次数的交换)。
证明:2N项来自于堆的构造(见上面命题)。2NlgN项来自于每次下沉操作最大可能需要2lgN次比较(见命题:一棵大小为N的完全二叉树的高度为└lgN┘;对于一个含有N个元素的基于堆的优先队列,插入元素操作只需不超过(lgN+1)次比较,删除最大元素的操作需要不超过2lgN次比较)。

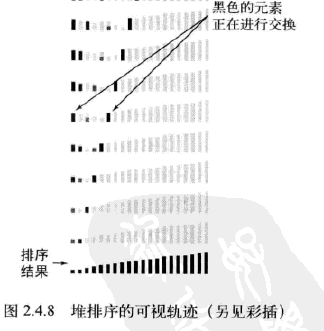
4.总结
堆排序在排序复杂性的研究中有着重要的地位,因为它是我们所知的唯一能够同时最优地利用空间和时间的方法——在最坏的情况下它也能保证使用~2NlgN次比较和恒定的额外空间。当空间十分紧张的时候(例如在嵌入式系统或低成本的移动设备中)它很流行,因为它只用几行就能实现(甚至机器码也是)较好的性能。但现代系统的许多应用很少使用它,因为它无法利用缓存。数组元素很少和相邻的其他元素进行比较,因此缓存未命中的次数要远远高于大多数比较都在相邻元素间进行的算法,如快速排序、归并排序,甚至是希尔排序。
另一方面,用堆实现的优先队列在现代应用程序中越来越重要,因为它能在插入操作和删除最大元素操作混合的动态场景中保证对数级别的运行时间。
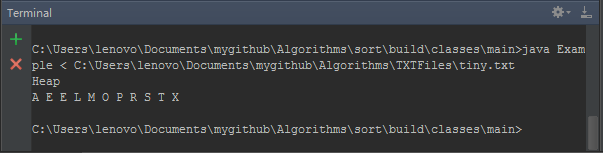
千万级
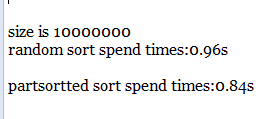
亿级,乱序和部分有序时间差不多

【源码下载】