算法导论--算法的概率分析技术

对于一个算法，它可能会出现最佳情况比如O(n)，也有可能出现最坏情况O(n^2)，但更多的可能是出现一般情况O(nlgn)。那么是否采用这个算法取决于它的平均情况，也就是它的期望值，这是一种概率分析手段。

下面就来具体介绍这种分析手段，前提假设您已经了解了离散数学的概率论的随机变量和期望值的相关内容。

【离散数学中的期望值是针对总的情况，一次的总的情况加上两次的总的情况加上三次的总的情况等；而算导里的指示器是跟踪每一次的情况，然后分别相加。】

以一个雇用问题来说明：

假设你需要雇用一名新的办公室助理。你先前的雇用尝试都以失败告终，所以你决定找一个雇用代理。雇用代理每天给你推荐一个应聘者。你会面试这个人，然后决定要不要雇用他。你必须付给雇用代理一小笔费用来面试应聘者。要真正地雇用一个应聘者则要花更多的钱，因为你必须辞掉目前的办公室助理，还要付一大笔中介费用给雇用代理。你的诺言是在任何时候，都要找到最佳人选来担任这项职务。因此，你决定在面试完每个应聘者后，如果这个应聘者比目前的办公助理更有资格，你就会辞掉目前的办公室助理，然后聘请这个新的应聘者。你愿意为这种策略而付出费用，但希望能够预测这种费用会是多少。

面试的费用较低，譬如说为c_i，而雇用的费用则较高，设为c_h。假设m是已雇用的人数。那么这个算法的总费用就是O(nc_i+mc_h)。不管雇用多少人，我们永远会面试n个应聘者，所以面试的费用永远是nc_i。因此，我们只专注于分析mc_h，即雇用的费用上。这个量在算法的每次执行中都会改变。

最坏情况分析

在最坏情况下，我们雇用了每个面试的应聘者。当应聘者的资质逐渐递增时，就会出现这种情况，此时我们雇用了n次，总的费用是O(nc_h)。

但是，较为合理的预期是应聘者并非总是以资质递增的次序出现的。事实上，我们既不能得知他们的出现次序，也不能控制这个次序。因此，通常我们预期的是一般或平均情况。

概率分析

概率分析是在问题的分析中应用概率技术。大多数情况下，我们使用概率分析来分析一个算法的运行时间。

指示器随机变量

指示器随机变量为概率与期望之间的转换提供了一个便利的方法。给定一个样本空间S和事件A，那么事件A对应的指示器随机变量I{A}定义为

举一个简单的例子，确定在抛一枚均匀硬币时正面朝上的期望次数。样本空间为S={H,T}，定义一个随机变量Y，取值H和T的概率各为1/2。接下来定义指示器随机变量X_H，它对应于硬币正面朝上的情况即事件H。这个变量计算抛硬币时正面朝上的次数，如果正面朝上则其值为1，否则为0。写作：

在抛硬币时正面朝上的期望次数，就是指示器变量X_H的期望值：

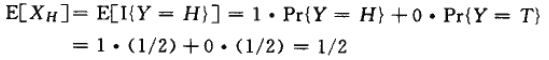
因此抛一枚均匀的硬币时，正面朝上的期望次数是1/2。如以下的引理所示，事件A对应的指示器随机变量的期望值等于事件A发生的概率。

我们令指示器随机变量X_i 对应于第i 次抛硬币时正面朝上的事件；令Y_i 表示第i 次抛硬币输出结果的随机变量，有X_i=I{Y_i=H}。假设随机变量X表示n次抛硬币中出现正面的总次数，于是

我们希望计算正面朝上的期望次数，所以我们使用对上面的等式两边取期望，得

等式左边是n个随机变量总和的期望值。有引理5.1，容易计算出每个随机变量的期望值。根据反映了期望的线性性质的公式E[X+Y]=E[X]+E[Y]，容易计算出总和的期望值：它等于n个随机变量期望值的总和。期望的线性性质利用了指示器随机变量作为有力的分析技术；即使随机变量之间存在依赖关系也成立。现在我们可以很容易地计算正面出现次数的期望值：

指示器随机变量极大地简化了计算过程。

利用指示器随机变量分析雇用问题

此时，我们希望计算雇用一个新的办公助理的期望次数。为了利用概率分析，假设应聘者以随机的顺序出现。令X作为一个随机变量，其值等于雇用一个新的办公助理的次数。

为了利用指示器随机变量，我们不是通过定义与雇用一个新的办公助理的次数对应的变量来计算E[X]，而是定义n个和每个应聘者是否被雇用对应的变量。特别地，令X_i 对应于第i 个应聘者被雇用这个事件的指示器随机变量。所以，

并且

由引理5.1，有

如果应聘者i 胜过从1到i-1的每一个应聘者，则应聘者i 会被雇用。由于已经假设应聘者以随机的顺序出现，所以前i 个应聘者也是以随机的顺序出现的。这些前i 个应聘者中的任何一个都等可能地是目前最有资格的。应聘者i 比从应聘者1到i-1更有资格的概率是1/i，因此也以1/i 的概率被雇用。由引理5.1，可以得出结论

现在可以计算E[X]了：

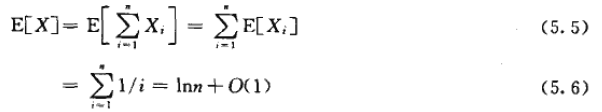
即使面试了n个人，平均起来看，实际上大约只雇用他们之中的lnn个人。